Yuanle Liu‘s Blog

Context Parallel 技术解析

9357 字
21 min read

学习链接

上下文并行（Context Parallel, CP）是一种面向大语言模型推理的并行策略，其核心思想是在序列（sequence length）维度上对输入和 KV Cache 进行分片来实现并行处理。与传统并行方式在每个设备上完整复制 Key–Value（KV）缓存不同，Context Parallel 将上下文 token 的 KV 缓存分布到多个设备上（通常采用交错分布），使每个设备仅存储并处理一部分 KV 缓存。在注意力计算过程中，各设备基于本地 KV 计算部分注意力贡献，并通过集合通信对结果进行聚合，从而在不改变注意力语义的前提下显著降低单卡的 KV 缓存显存开销，特别适用于长上下文解码场景。该设计以增加通信为代价，显著降低了单设备的 KV 缓存内存需求，并保持了注意力计算的数值一致性。

上下文并行（Context Parallel, CP）是一类面向大语言模型长上下文推理的并行技术，其目标是在不改变注意力语义与数值结果的前提下，把注意力计算中最昂贵、最占显存的“上下文维度工作量”（尤其是 KV cache 的存储与访问）分摊到多张 GPU 上。与传统张量并行（TP）按头切分不同，CP 主要沿 sequence / context 维度组织并行：将上下文 token 对应的 KV 表示按序列位置切分并分布到多个设备（可采用交错或块状布局），使单卡仅持有全局 KV 的一个子集，从而显著降低长上下文场景下单卡 KV cache 的显存占用。

在计算层面，CP 的关键在于将注意力 Softmax 重写为可分片、可合并的形式：每个设备仅基于本地 KV 分片计算局部的注意力统计量与部分输出（可理解为对 (m,l,om, l, o) 三元组的局部贡献，其中 mm 为局部最大值、ll 为指数和、oo 为未归一化的加权和值），再通过跨设备通信将这些局部贡献按稳定的 Max–Sum / LSE 规则合并，最终得到与单卡全量 KV 注意力严格一致的输出。

CP 在工程上可以呈现为不同阶段/通信模式的实例：例如 DCP 在解码阶段将增长的 KV cache 沿序列维度分片以消除复制，并在每步解码时用少量 all-reduce 合并局部注意力结果；而在预填充阶段，CP 可通过 PCP 的分块注意力合并或 RingAttention 的环形流水线交换 KV 分片实现并行。总体而言，CP 用一定的通信与实现复杂度换取显存占用的大幅下降与长上下文推理吞吐/延迟的改善，尤其适用于超长上下文与多卡部署场景。

一、Self-Attention 回顾

大语言模型的核心是自注意力机制（Self-Attention）。在 Transformer 的每一层中，输入序列的隐藏表示会通过线性变换生成查询、键、值张量（Query、Key、Value，简称 Q、K、V）。然后计算注意力分数矩阵：每个查询向量与所有键向量点积，得到对应的相关性分数。简化公式如下：

Score(i,j)=Qi⋅KjT,Score(i, j) = Qi ⋅ K_j^T,

其中 QiQ_i 是第 ii 个查询向量，KjK_j 是第 jj 个键向量。将分数除以 d\sqrt{d}（dd 为每个头的维度）进行缩放后，对每一行应用 Softmax 得到注意力权重矩阵 Attention Weight。再利用权重对值向量加权求和，得到注意力输出：

AttnOutputi=∑jSoftmax(Scorei)j⋅Vj\text{AttnOutput}_{i} = \sum_{j}^{}\text{Softmax}\left( \text{Score}_{i} \right)_{j} \cdot V_{j}

上述过程即单头注意力计算的数学原理。多头注意力（Multi-Head Attention）则是将隐藏维度拆分成多个头并行计算，然后将各头的输出拼接。**KV 缓存（Key-Value Cache，KV 缓存）**是在解码阶段保存历史生成的 KK、VV 张量，以避免重复计算。每生成一个新 token，其查询向量将与缓存中的所有键进行计算，从而关注到先前的上下文信息。常规自注意力在单块 GPU 上的计算流程：所有的 Q、K、V 全部在同一设备上处理，输出完整的注意力结果 O，每个查询向量与同一序列中的所有键值进行计算。

这时计算的时间复杂度为 O(seq_len2⋅dmodel)O(\text{seq\_len}^2 \cdot d_{\text{model}})（序列长度平方级），因此当序列长度 TT 很大时，自注意力的计算和内存开销会急剧增长。在推理中，若直接在单卡上处理超长序列，上述 T2T^2 复杂度将成为主要瓶颈。这正是引出“上下文并行（Context Parallel）”技术的背景：如何在保证注意力精确等价的前提下，将长序列的注意力计算分摊到多张卡上，以突破单卡内存和算力限制。

二、Prefill vs Decode Stage Characteristics

LLM 推理过程分为两个阶段：预填充阶段（Prefill 阶段）和解码阶段（Decode 阶段）。预填充阶段指模型接受完整输入 Prompt 后，在生成第一个输出 token 之前，对整条输入序列进行一次性前向计算；解码阶段则是在预填充完成后，模型进入自回归生成，每次只推理一个新 token，直到得到完整输出。这两个阶段的计算模式和性能侧重截然不同：

  • 预填充阶段 (Prefill Stage)：一次性并行处理 TT 个输入 token，计算量大但延迟（Latency）较高。由于可以并行利用 GPU 算力处理整个输入序列，此阶段通常能高效利用 GPU，但如果输入长度很长，首个 token 输出前的等待时间（即首字节延迟/首个 token 延迟，TTFT, Time to First Token）也会比较长。预填充阶段的主要产出是填充好的 KV 缓存，它存储了输入 Prompt 所有 token 的 Key/Value 表示，供后续解码阶段高速查阅。
  • 解码阶段 (Decode Stage)：模型依据预填充阶段得到的上下文，逐步生成后续 token。每步只处理 1 个新 token，计算开销相对较小，单步延迟低，但由于只能串行生成，GPU 利用率往往不高。批量调度（Batching）在解码阶段非常关键，它通过并行推理多个请求来提高整体吞吐量（Throughput）。在解码过程中，KV 缓存会不断增长，每产生一个新 token 就将其键和值追加进去，以供下次注意力计算使用。因此解码阶段的内存需求随着生成长度线性上升。

上述两阶段存在性能目标上的差异：预填充更关注降低首 token 延迟（尽快产生第一个输出），而解码更关注提升吞吐（同时服务更多 token /更多请求）。针对这两个阶段，将采取不同的并行策略，实现上下文并行分别优化它们。简单来说，预填充阶段采用上下文并行是为了在多卡上摊分大 prompt 的计算，减少单卡等待；解码阶段采用上下文并行是为了在多卡上存储/计算长上下文的注意力，突破单卡KV缓存容量限制。

三、Decode Context Parallel

解码上下文并行（Decode Context Parallel, DCP）专注于加速解码阶段的长上下文处理和减小内存开销。在解码时，每一步需要针对海量的 KV 缓存（即累计的上下文 tokens）计算当前少量查询。例如某模型有 HH 个注意力头（kv-head），上下文长度为 TT，那么 KV 缓存中需要存储 H×TH \times T 个键/值表示。如果使用张量并行（Tensor Parallel, TP）在多卡间按注意力头数 HH 切分模型参数，那么当并行卡数超过 HH 时，多余的 GPU 无法进一步切分 KV 缓存，只能复制整个 KV 缓存到这些卡上，造成内存浪费。

例如模型有 8 个注意力头而使用 TP=16，则每份 KV 缓存被复制 2 倍，以服务不同 GPU 上的查询头。复制虽然避免了通信但极大降低了内存利用效率。DCP 的思路是在不增加总GPU数量的前提下，按序列长度维度对 KV 缓存再做切分，消除重复存储。

并行层级设计：

  • Context Parallel（CP）被设计为一种嵌套于 Tensor Parallel（TP）之内的并行维度，用于沿上下文（token / sequence）维度切分注意力计算。其并行层级组织依次嵌套为：Data Parallel > Tensor Parallel > Context Parallel
  • 每个 GPU 同时隶属于一个 TP group 与一个 CP group，并分别持有对应的 tp_rank 与 cp_rank。并行配置需满足：tp_size % cp_size == 0。Context Parallel 本身不改变全局 world size，而是在 TP group 内部进一步细分通信与数据归属。

具体而言，假设张量并行使用了 NTPN_{\text{TP}} 张卡（模型按头分在这些卡上）。我们可以选择一个 DCP 大小 NDCPN_{\text{DCP}}（满足 1≤NDCP≤NTPH1 \le N_{\text{DCP}} \le \frac{N_{\text{TP}}}{H}），将每卡需存储的 KV 长度减少到原来的 1NDCP\frac{1}{N_{\text{DCP}}}，从而将 KV 缓存进一步均匀分布到 NTP×NDCPN_{\text{TP}} \times N_{\text{DCP}} 张卡上。实际上，vLLM 的实现是让 DCP 在 TP 域内部形成分组：每组 TP 内的 NDCPN_{\text{DCP}} 张卡负责共享原本属于该组的 KV 缓存。这样设置 -dcp N 后，并没有增加需要启动的 GPU 总数，而是降低了每卡持有的 KV 缓存份量，减少了 KV 重复。DCP 大小越大，每份KV缓存重复的次数越少，节省显存越多，但同时注意力计算的跨卡通信开销增加。因此，最佳的 DCP 配置需要在内存和通信开销间折中，通常先尽量增大 TP 直到受限，再逐步提高 DCP 大小以去除剩余复制。

**KV 缓存的切分策略：vLLM 采用交错分片（interleaving）**将上下文 token 按顺序交错地分配到不同 GPU 的 KV 缓存段中。对于 token 索引 t，将其存储在 t % dcp_size == dcp_rank 的设备上。例如有 2 卡 DCP，序列位置奇数 token 的 KV 存一张卡，偶数 token 存另一张卡。交错方式保证当序列增长时，新 token 能自然地按轮转附加到各卡的缓存后面，无需重新分片。这种方法最早由 Chao Hong 等人在 Helix Parallelism 中提出（Helix是一种解码加速并行策略，稍后会简述）。

多卡注意力计算：使用 DCP 后，每步解码时每张 GPU 仅持有整个 KV 缓存的一部分（比如一半 token 的 KV）。但为了正确计算注意力，每个新查询向量需要“看见”全局的所有键和值。vLLM 巧妙地通过算法在多卡上并行完成等价的计算，而无需真的将完整 KV 集中到一张卡上。过程如下：每张 GPU 基于本地 KV 分片计算部分注意力输出，然后在 GPU 组内通过通信合并这些部分输出，重构出与单卡计算完全一致的结果。

具体来说，在 DCP 中，单步 decode attention 的计算流程如下：

  1. 本地 attention 不直接感知 Context Parallel，每个设备仅基于其本地 KV 子集，计算局部 attention 统计量，包括：
    • logits 的局部最大值；
    • 局部指数和；
    • 局部加权输出向量。
  2. 跨设备规约（Collective Communication）通过 CP group 内的集合通信操作完成：
    • 全局最大值的规约（用于数值稳定的 softmax）；
    • 全局归一化因子的规约。
  3. 输出合成
    • 各设备基于全局归一化因子对局部输出进行归一化，并通过求和恢复与单设备 attention 完全一致的结果。

该流程确保 attention 的数学语义保持不变，拆分仅发生在计算过程层面。下面再用伪代码和公式分步说明其机制：

python
# ============================================================
# DCP Decode: one decode step (new token), multi-head self-attn
# Exact attention (numerically identical to single-GPU)
# Supports MHA / GQA / MQA via head-mapping
# ============================================================
# -----------------------------
# Shapes / notation
# -----------------------------
# B   : batch size
# Hq  : number of query heads
# Hk  : number of KV heads (Hk = Hq for MHA; < Hq for GQA/MQA)
# D   : head dimension
# T_r : number of tokens in this DCP rank's KV shard
#
# Q    : [B, Hq, D]
# K_r  : [B, Hk, T_r, D]
# V_r  : [B, Hk, T_r, D]
#
# group(hq) -> hk : query-head to kv-head mapping
#   - MHA: group(hq) = hq
#   - GQA/MQA: multiple hq map to the same hk
#
# All-reduce ops are over the DCP process group only.
# ============================================================
# Step 0: allocate per-rank buffers
# ============================================================
m_r = zeros([B, Hq])          # local max per (batch, query-head)
l_r = zeros([B, Hq])          # local exp-sum per (batch, query-head)
o_r = zeros([B, Hq, D])       # local weighted sum per (batch, query-head)
# ============================================================
# Step 1: local attention statistics per query head
# ============================================================
for hq in range(Hq):
    hk = group(hq)  # map query head -> KV head
    # Compute local scores against this rank's KV shard
    # S_r: [B, T_r]
    S_r = matmul(
        Q[:, hq, :],                 # [B, D]
        transpose(K_r[:, hk, :, :])  # [B, D, T_r]
    )
    # (Optional) apply causal / padding mask here on S_r
    # Local max over shard (for numerical stability)
    m_r[:, hq] = max(S_r, axis=-1)          # [B]
    # Stable exponentials (NOT globally normalized)
    P_r = exp(S_r - m_r[:, hq][:, None])    # [B, T_r]
    # Local exp-sum
    l_r[:, hq] = sum(P_r, axis=-1)          # [B]
    # Local weighted value sum
    # o_r[b, hq, :] = sum_t P_r[b, t] * V_r[b, hk, t, :]
    o_r[:, hq, :] = matmul(
        P_r,                                # [B, T_r]
        V_r[:, hk, :, :]                    # [B, T_r, D]
    )
# ============================================================
# Step 2: all-reduce MAX to get global max per (B, Hq)
# ============================================================
m = all_reduce_max(m_r)        # [B, Hq]
# ============================================================
# Step 3: rescale local stats into global-max reference
#         alpha_r = exp(m_r - m)
# ============================================================
alpha_r = exp(m_r - m)         # [B, Hq]
l_r_hat = alpha_r * l_r                    # [B, Hq]
o_r_hat = alpha_r[..., None] * o_r         # [B, Hq, D]
# ============================================================
# Step 4: all-reduce SUM to get global numerator / denominator
# ============================================================
l = all_reduce_sum(l_r_hat)    # [B, Hq]
o = all_reduce_sum(o_r_hat)    # [B, Hq, D]
# ============================================================
# Step 5: final normalized attention output
# ============================================================
attn_out = o / l[..., None]    # [B, Hq, D]
# ============================================================
# (Optional) log-sum-exp (LSE), useful for backward / fusion
# ============================================================
lse = m + log(l)               # [B, Hq]
# ============================================================
# Outputs:
#   attn_out : [B, Hq, D]   exact self-attention output
#   lse      : [B, Hq]      per-query-head log-sum-exp
# ============================================================
# ============================================================
# DCP Decode: one decode step (new token), multi-head self-attn
# Exact attention (numerically identical to single-GPU)
# Supports MHA / GQA / MQA via head-mapping
# ============================================================
# -----------------------------
# Shapes / notation
# -----------------------------
# B   : batch size
# Hq  : number of query heads
# Hk  : number of KV heads (Hk = Hq for MHA; < Hq for GQA/MQA)
# D   : head dimension
# T_r : number of tokens in this DCP rank's KV shard
#
# Q    : [B, Hq, D]
# K_r  : [B, Hk, T_r, D]
# V_r  : [B, Hk, T_r, D]
#
# group(hq) -> hk : query-head to kv-head mapping
#   - MHA: group(hq) = hq
#   - GQA/MQA: multiple hq map to the same hk
#
# All-reduce ops are over the DCP process group only.
# ============================================================
# Step 0: allocate per-rank buffers
# ============================================================
m_r = zeros([B, Hq])          # local max per (batch, query-head)
l_r = zeros([B, Hq])          # local exp-sum per (batch, query-head)
o_r = zeros([B, Hq, D])       # local weighted sum per (batch, query-head)
# ============================================================
# Step 1: local attention statistics per query head
# ============================================================
for hq in range(Hq):
    hk = group(hq)  # map query head -> KV head
    # Compute local scores against this rank's KV shard
    # S_r: [B, T_r]
    S_r = matmul(
        Q[:, hq, :],                 # [B, D]
        transpose(K_r[:, hk, :, :])  # [B, D, T_r]
    )
    # (Optional) apply causal / padding mask here on S_r
    # Local max over shard (for numerical stability)
    m_r[:, hq] = max(S_r, axis=-1)          # [B]
    # Stable exponentials (NOT globally normalized)
    P_r = exp(S_r - m_r[:, hq][:, None])    # [B, T_r]
    # Local exp-sum
    l_r[:, hq] = sum(P_r, axis=-1)          # [B]
    # Local weighted value sum
    # o_r[b, hq, :] = sum_t P_r[b, t] * V_r[b, hk, t, :]
    o_r[:, hq, :] = matmul(
        P_r,                                # [B, T_r]
        V_r[:, hk, :, :]                    # [B, T_r, D]
    )
# ============================================================
# Step 2: all-reduce MAX to get global max per (B, Hq)
# ============================================================
m = all_reduce_max(m_r)        # [B, Hq]
# ============================================================
# Step 3: rescale local stats into global-max reference
#         alpha_r = exp(m_r - m)
# ============================================================
alpha_r = exp(m_r - m)         # [B, Hq]
l_r_hat = alpha_r * l_r                    # [B, Hq]
o_r_hat = alpha_r[..., None] * o_r         # [B, Hq, D]
# ============================================================
# Step 4: all-reduce SUM to get global numerator / denominator
# ============================================================
l = all_reduce_sum(l_r_hat)    # [B, Hq]
o = all_reduce_sum(o_r_hat)    # [B, Hq, D]
# ============================================================
# Step 5: final normalized attention output
# ============================================================
attn_out = o / l[..., None]    # [B, Hq, D]
# ============================================================
# (Optional) log-sum-exp (LSE), useful for backward / fusion
# ============================================================
lse = m + log(l)               # [B, Hq]
# ============================================================
# Outputs:
#   attn_out : [B, Hq, D]   exact self-attention output
#   lse      : [B, Hq]      per-query-head log-sum-exp
# ============================================================

上述伪代码展示了 Softmax 合并计算的过程，合并公式本质上是：

m=max⁡rmr,l=∑remr−m lr,o=∑remr−m or,out=ol,lse=m+log⁡lm=\max_r m_r,\quad l=\sum_r e^{m_r-m}\,l_r,\quad o=\sum_r e^{m_r-m}\,o_r,\quad \text{out}=\frac{o}{l},\quad \text{lse}=m+\log l

各 GPU（rank）先在本地 KV 分片上完成一次“完整的局部注意力贡献计算”：对本地分片算出局部 score，并得到三类可合并的中间量——局部最大值 mrm_r、局部指数和 lrl_r，以及基于同一数值基准得到的局部“未归一化加权和” oro_r（也就是本 rank 对最终 attention output 的贡献，只是尚未做全局归一化）。关键点在于 Softmax 的数值稳定合并：先做一次 All-Reduce(Max) 得到全局最大值

m=max⁡rmrm=\max_r m_r

然后每个 rank 用缩放因子 αr=exp⁡(mr−m)\alpha_r=\exp(m_r-m) 把自己的 (lr,or)(l_r,o_r) 统一到同一个全局基准上，得到

l^r=αr lr,o^r=αr or\hat l_r=\alpha_r\,l_r,\qquad \hat o_r=\alpha_r\,o_r

接着分别对 l^r\hat l_r 和 o^r\hat o_r 做 All-Reduce(Sum) 得到全局

l=∑rl^r,o=∑ro^rl=\sum_r \hat l_r,\qquad o=\sum_r \hat o_r

最终输出与单卡完全一致：

attn_out=ol,LSE=m+log⁡l\text{attn\_out}=\frac{o}{l},\qquad \text{LSE}=m+\log l

由于通信只发生在“必要的统计量与聚合量”上：一次全局最大值（mm）、一次全局指数和（ll）以及一次输出向量聚合（oo），因此通信量只与 query token 数和隐藏维度相关，而不随上下文长度增长，从而能够扩展到百万级上下文长度。

在完成上述合并后，每张卡都得到了当前解码步的完整注意力输出向量。总的来说，通过 DCP，vLLM 实现在解码阶段分片存储和并行访问 KV 缓存，使多 GPU 协同完成与单 GPU 相同的注意力计算。这样就显著扩展了可支持的上下文长度和并发请求数量，同时在一定程度上牺牲了一些通信开销。实际应用中，可以先增大 TP 以加速 FFN 计算，再酌情引入 DCP 来分担 KV 缓存，以在显存容量和通信成本间取得平衡。

四、Prefill Context Parallel

预填充上下文并行（Prefill Context Parallel, PCP）旨在降低预填充阶段处理超长 Prompt 时的延迟，提高首个输出 token 的产生速度。在预填充阶段，需要对长度可能非常长的输入序列一次性前向计算，这对单个 GPU 而言可能计算开销巨大且内存压力很高。PCP 通过将一次性的大计算切分到多张 GPU 上并行完成，将预填充时间摊薄。具体策略有两种：

  • 部分查询，完整键/值 (Partial Q, Full KV)

    适用于输入长度中等（单卡勉强容纳完整 KV）的情况，目标是加速预填充计算。做法是将输入序列平均切分为 NN 段，每个 GPU 负责计算自己那一段的新 token 的 Q、K、V 张量。随后，通过一次 All-Gather 通信将所有 GPU 计算得到的键、值张量汇总，使每张卡都持有整条序列的 K/V。这样，每个 GPU 就可以独立计算其负责的查询 tokens 的注意力输出，但在注意力计算时使用的是全序列的完整 K/V（需要对超出本段的未来位置做 mask 掩码，确保因果性）。最终，各 GPU 算出的输出拼接起来，就是与单卡从头算到尾相同的结果。

    由于计算任务被拆分为 NN 份并行执行，预填充的总耗时大幅下降，可近似降低到原来的 1N\frac{1}{N}（加上一次聚合通信开销）。这种策略的开销主要在于 All-Gather 汇总 K/V，使每卡内存临时需要放下一份完整 KV。因此它适用于“KV 尚可放下、要求尽量降低延迟”的场景。vLLM 实现中将此模式作为 PCP 的基本方案之一。

  • 部分查询，部分键/值 (Partial Q, Partial KV)

    当输入序列极长、单卡无法容纳完整 KV 时，必须进一步限制内存占用。此时每张 GPU 只保留自己负责的那段的 K/V，不做全量汇总，而是采用一种被称为 Ring Attention（环形注意力） 的通信算法。其思想是在计算注意力时，各 GPU 逐块交换彼此持有的 KV 片段，边传输边计算，从而最终每张卡都“看过”整条序列的 KV 但从未完整地存下全部 KV。具体流程如下：假设有 NN 张 GPU，序列被分成 NN 段。第 1 步，各 GPU 仅使用自己的本地 KV 计算对应查询片段的注意力输出“块”O(0)O^{(0)}；接着，每个 GPU 将自己的 KV 块发送给下一个 GPU（同时接收上一 GPU 的 KV 块）。第 2 步，各 GPU 拿到新的他人 KV 块，计算自己查询的下一部分注意力输出 O(1)O^{(1)}，再执行下一轮环形传输……如此进行 N−1N-1 次，直至每段查询都依次与所有 KV 块计算过注意力。最后将同一路径上的 NN 次部分输出累加，即得到完整的注意力结果。为了确保精度，在每轮计算后需对中间输出进行一次 log-sum-exp 校正（对应 Softmax 的分段归一化）。

    整个 Ring Attention 过程通过将通信和计算重叠（Overlap）实现了高效并行：只要 KV 块传输时间小于下一块计算时间，就不会产生额外延迟。也就是说，通信几乎被完全隐藏在计算过程中，使得多卡协同计算长序列注意力时的总用时近似等于纯计算用时。这种“块状环形并行”策略可以在线性扩展序列长度的同时，保持接近线性的吞吐提升。Berkeley 等机构的研究表明，利用 Ring Attention 可以在训练和推理中将 Transformer 上下文长度扩展到接近“设备数量 × 原始长度”，实现近乎无限长的上下文处理能力。vLLM 对 Ring Attention 的支持还在积极开发中，目前的实现主要聚焦于前一种 All-Gather 策略，而对于极限长度场景将逐步引入 Ring Attention 机制。

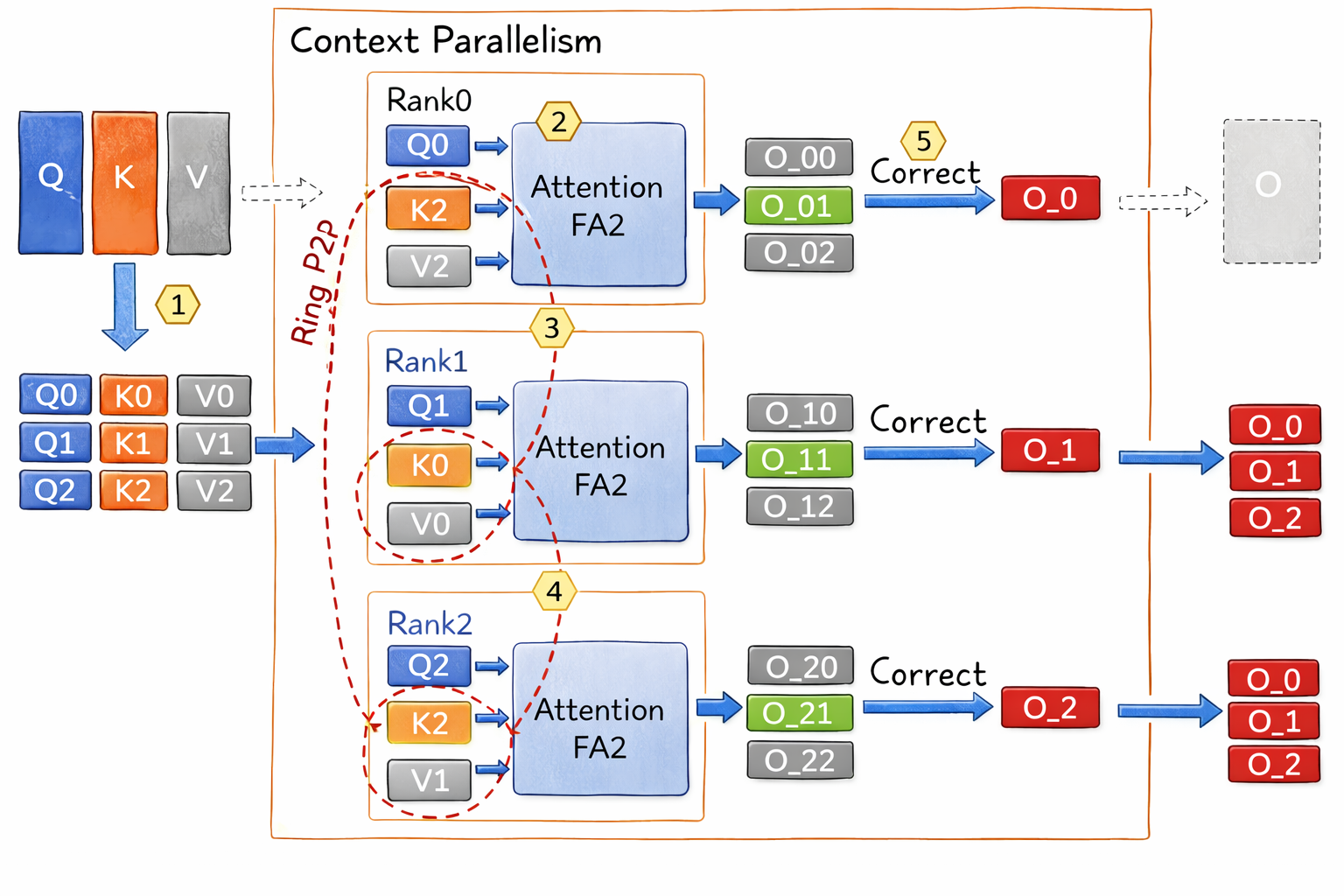
图2：预填充上下文并行的 Ring Attention 流程示意（部分查询，部分 KV 的场景）。左侧橙/灰色块表示不同 GPU 持有的键、值片段（K0/K1/K2 和 V0/V1/V2）；紫色框表示各 GPU 独立执行注意力计算模块。流程: ①各 GPU 先用本地 K/V 计算自己的查询块（Q0/Q1/Q2）的注意力输出 (O_00, O_11, O_22)；② 然后按环形拓扑将本地 K/V 发送给下一个 GPU（红色箭头），同时接收来自上一个 GPU 的 K/V；③ 重复计算下一轮注意力输出 (如 Rank0 计算 O_01，Rank1 计算 O_12，Rank2 计算 O_20)，共进行 N-1 轮通信+计算；④ 每轮计算后对局部输出进行 LogSumExp 校正以准备合并；⑤ 所有分块结果通过累加校正得到最终输出 O（红色块）。整个过程中通信与计算充分重叠，实现了无额外开销的近线性扩展。

需要注意的是，在 PCP 与 Ring Attention 结合使用的预填充阶段，上下文并行不再依赖对同一 token 的非注意力模块进行重复计算，而是通过在序列维度同时切分 Q、K、V，使每个 GPU 仅处理其负责的 token 子序列，从而避免了前馈层、LayerNorm 等非注意力计算的冗余。各 GPU 在本地完成 embedding、FFN 与 QKV 投影后，通过 Ring Attention 的环形通信机制逐步交换 K/V 分片，并以稳定的 LSE / Max-Sum 形式累积注意力统计量，实现与单卡等价的全上下文注意力结果。由于预填充阶段的主要计算瓶颈来自注意力随上下文长度增长的 O(T2)O(T^2) 复杂度，该方式能够在不引入额外冗余计算的前提下，将超长序列的注意力计算均匀分摊到多 GPU 上。随着上下文规模增大，通信开销相较于被并行化的计算量增长更为缓慢，使得该方案在极长 Prompt 场景下仍具备良好的扩展性。

目前，PCP 与 Ring Attention 的结合仍处于持续探索和工程化阶段，未来有望与 Chunked Prefill 等机制进一步协同，以提升超长 Prompt 场景下的整体吞吐能力。总体而言，通过在预填充阶段采用 PCP + Ring Attention 的序列并行策略，并在解码阶段配合 DCP 提升并发与显存效率，系统能够在长上下文推理场景下同时兼顾低首 token 延迟与高吞吐性能。

五、Ring Attention 算法与 Softmax 合并机制

在上下文并行的实现中，Ring Attention 并不是一次性将完整的 KV 收集到本地再计算注意力，而是将注意力计算拆解为一系列可逐步累积的局部计算与通信步骤。其核心思想是：

注意力的 Softmax 可以被分解为可合并的中间统计量，从而支持分块计算与顺序累积。

5.1 Ring Attention 的计算–通信流程

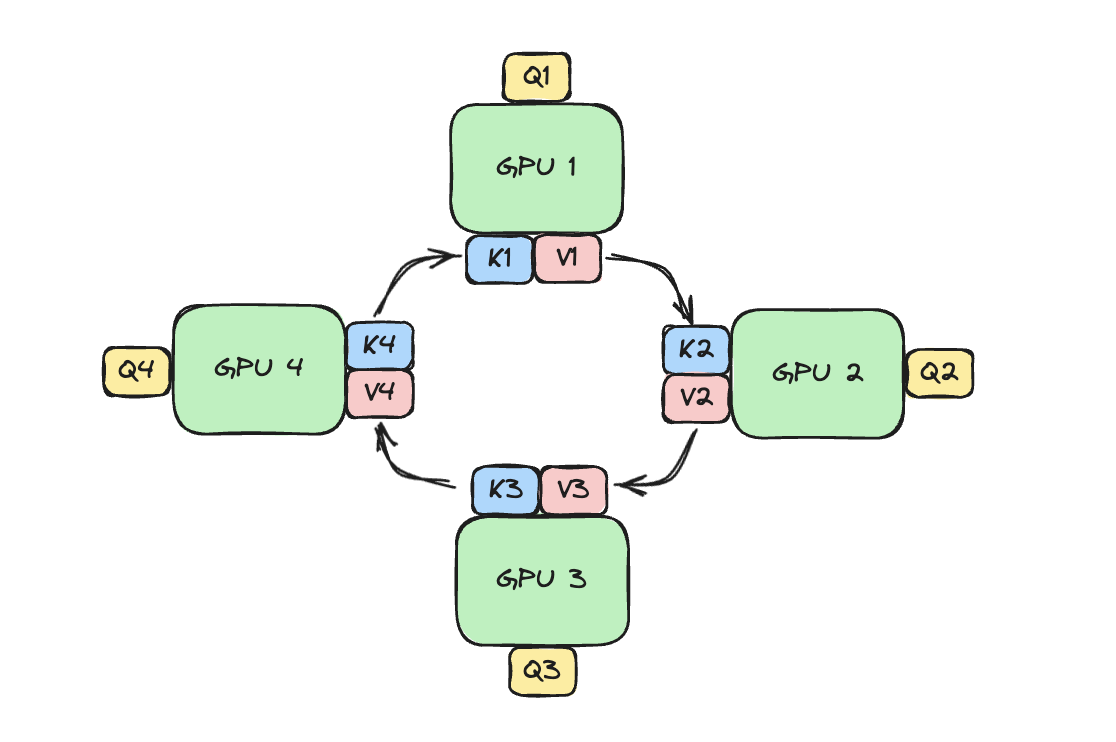
在 Ring Attention 中，序列被按 token 维度切分到不同 GPU 上，每个 GPU 仅持有自己负责的 token 子序列的 Q/K/V。注意力计算不再是“先收集全部 KV 再算”，而是以 环形（ring）方式逐步交换 KV 分片并同步进行计算。具体而言，对某一 GPU 来说：

  1. 初始化阶段

    GPU 持有本地的 Q_local, K_local, V_local，并初始化注意力累积状态：

    • 当前最大值 m = -∞
    • 当前指数和 l = 0
    • 当前未归一化输出向量 o = 0

  2. 每一轮 ring step（处理一个 KV 分片）

    • 使用本地的 Q_local 与当前收到的 K_block 计算 score

    • 得到该分片上的局部最大值 m_block

    • 将 (m, l, o) 与当前分片的结果通过 Max-Sum 规则合并：

      python
      m_new = max(m, m_block)
l_new = exp(m - m_new) * l + exp(m_block - m_new) * l_block
o_new = exp(m - m_new) * o + exp(m_block - m_new) * o_block
      m_new = max(m, m_block)
l_new = exp(m - m_new) * l + exp(m_block - m_new) * l_block
o_new = exp(m - m_new) * o + exp(m_block - m_new) * o_block

    • 更新 (m, l, o)

    • 同时将当前的 KV 分片发送给 ring 中的下一个 GPU，并接收新的 KV 分片

  3. 流水线执行

    通信与计算是重叠的：当一个 KV 分片在网络中传输时，GPU 已经开始对上一个分片进行 attention 计算，从而将通信延迟隐藏在计算中。

经过完整一圈 ring 之后，每个 GPU 都完成了对 全序列 KV 的注意力累积，并且得到了一组与单卡 Softmax 等价的 (m, l, o)。

5.2 Softmax 合并的工程等价形式

从工程实现角度看，Ring Attention 并不会显式构造全局 Softmax 权重，而是始终在维护三类 可合并统计量：

  • m：当前已处理 KV 分片上的全局最大 score
  • l：基于 m 的指数和（即 Softmax 分母）
  • o：未归一化的加权和值（即 Softmax 分子）

最终注意力输出仅需一次归一化即可得到：

python
attn_out = o / l
lse      = m + log(l)
attn_out = o / l
lse      = m + log(l)

这种写法与单卡 Softmax 在数学上严格等价，但在计算顺序上允许：

  • KV 被任意切分
  • KV 分片按任意顺序处理
  • 中间结果通过稳定的 Max-Sum 规则逐步合并

因此，无论是在 Ring Attention 的顺序累积，还是在 PCP / DCP 中的并行归约，最终结果都与未切分情况下的注意力输出完全一致。

从工程视角看，上下文并行的关键并不在于如何切分 KV，而在于将 Softmax 重写为一组可稳定合并的统计量，使注意力计算能够在任意分片顺序和并行模式下逐步累积而不损失精度。

维度Ring Attention + PCP普通 PCPDCP
Q 是否切分✅❌❌
KV 是否切分✅✅✅
m–l–o 产生每个 ring step每个 rank每个 rank
m–l–o 合并顺序累积All-ReduceAll-Reduce
合并频率多轮一次每 decode step
冗余 FFN❌✅❌
典型阶段PrefillPrefillDecode

六、PCP + Ring Attention 中的负载均衡问题

在理论层面，Prefill Context Parallel（PCP）与 Ring Attention 的组合，解决的是超长上下文下 attention 计算与显存容量不可扩展的问题。但在工程实现中，如果不额外考虑负载均衡，这一组合往往会性能严重退化，甚至不如不开启并行。其根本原因并不在通信，而在 causal attention 的计算分布本身是强烈不均匀的。

6.1 负载不均衡从何而来：Causal Attention 的“位置偏置”

在自回归模型中，attention 计算遵循因果掩码（causal mask）：第 tt 个 token 只能 attend 到 [0,t][0,t] 的 KV。

这意味着，对单个 query token 的 attention 计算量近似与其 绝对位置 成正比：cost(qt)  ∝  t\text{cost}(q_t) \;\propto\; t。

如果我们在 PCP 中 简单按连续区间（contiguous）切分序列：

  • rank0 负责 [0,T/4)[0,T/4)
  • rank3 负责 [3T/4,T)[3T/4,T)

那么虽然 token 数量相同，但 rank3 的 attention FLOPs 会远高于 rank0。

6.2 为什么 Ring Attention 会放大这个问题

如果只是普通 PCP（AllGather KV、各算各的），负载不均衡主要表现为：

  • 某些 GPU 算得久一点
  • 但总体还能接受

而在 Ring Attention 中，这种不均衡会被结构性放大。Ring Attention 的时间节拍约束，其执行模式是一个强同步的流水线：

  • 每一轮（step）
    • 每个 rank 用当前收到的 KV block 对本地 Q block 计算 partial attention
    • 同时将自己的 KV block 发送给下一个 rank
  • 所有 rank 必须在本轮完成后 才能进入下一轮

因此，每一轮的实际耗时是：

Tstep  =  max⁡r(Tcompute(r),Tcomm(r))T_{\text{step}} \;=\; \max_r \left( T^{(r)}_{\text{compute}}, T^{(r)}_{\text{comm}} \right)

也就是说，只要有一个 rank 计算明显更慢，它就会成为整个 ring 的节拍上限。

当 PCP 采用 contiguous 切分时：

  • 承担“后段 query”的 rank 在每一轮的 compute 都更重
  • 其他 rank 即使早早算完，也只能空等

最终结果是：

  • Ring pipeline 出现大量 bubble
  • 通信与计算 overlap 被破坏

6.3 负载均衡的核心思想：让每个 rank 同时“轻 + 重”

要解决这个问题，必须回到 attention 工作量的本质分布：attention 的工作量不是“按 token 数均匀”，而是“按 token 位置递增”。

因此，真正合理的切分目标不是每个 rank 拿到相同数量的 token，而是每个 rank 拿到相近的 attention 工作量积分。

6.4 工程解法：对称切分

vLLM 在 PCP + Ring Attention 相关设计中，采用了一种极其工程化但非常有效的负载均衡策略，通常称为 对称切分（mirror / symmetric partition）。

设 PCP 并行度为 NN，将整个序列切分为 2N2N 个连续 chunk：

chunks={0,1,…,2N−1}\text{chunks} = \{0, 1, \dots, 2N-1\}

然后令第 rr 个 rank 负责：

chunks(r)={ r,  2N−1−r }\text{chunks}(r) = \{\, r,\; 2N-1-r \,\}

也就是说：

  • 每个 rank 同时拿到一个前段 chunk（轻）
  • 以及一个对称的后段 chunk（重）

从而使 每个 rank 的总 attention FLOPs 接近一致。

6.5 进一步负载均衡细节

在真实系统中，对称切分通常还会与以下策略组合使用：

  • Block 粒度调节

    text
    工程上会选择 block size，使得：
    工程上会选择 block size，使得：
    Tcompute(block)  ≈  Tcomm(block)T_{\text{compute}}(\text{block}) \;\approx\; T_{\text{comm}}(\text{block})

    ，以保证每一轮 ring step 都能高效 overlap。

  • Batch 内按 token 总量而非请求数切分

    在 serving 场景下，请求长度不一致，如果只按 request 切分，会再次引入负载不均。因此实际系统通常：

    • 将 batch 展平成 token segments
    • 按 token 数 + 位置加权进行切分

七、Implementation in vLLM and Overall Architecture

在 vLLM 中，上下文并行作为模型并行的一种新维度，与数据并行、张量并行等正交存在。其实现涉及通信域的划分和调度策略的调整：

  • 通信域与资源分配

    vLLM 使用基于 NCCL 的通信原语实现 DCP/PCP 所需的 All-Gather/All-Reduce。DCP 的通信组被构造为在每个 TP 组内部进一步细分的子组；而 PCP 的通信组则是与 DP、TP 并列的新一级分组，会影响总 GPU 使用数量。这意味着用户在启动服务时需综合考虑 DP（模型副本数）、TP（分片数）、PP（流水线并行层数）以及 PCP（预填充分片）几个参数来确定集群中各角色 GPU 的分配。例如，在 8 卡单机中使用 tp 4 -dcp 2 -pcp 2，表示模型用 4 卡做张量并行，每组 TP 内再 2 卡做解码上下文并行，同时预填充也跨 2 卡并行执行（PCP 组在此简单情况下可能等同于整个 DP 组大小）。vLLM 通过类似 MPI 子通信域的方式管理这些组合并行策略，使各并行域互不干扰地协调工作。

  • KV 缓存槽映射 (Slot Mapping)

    为支持上下文并行，vLLM 对 KV 缓存的存储结构进行了调整。DCP 引入了“虚拟块（virtual blocks）”的概念，将逻辑上的一个请求的 KV 缓存映射到实际多个设备的内存槽上。PCP 在此基础上进一步细分，每个 PCP 组仅存储该组负责的那段序列的 KV。调度器据此维护一个全局 Slot Mapping 表，记录每个请求的每段上下文在哪些 GPU 的哪个位置。这样，在解码阶段需要读取某 token 的 KV 时，可以快速定位到对应 GPU 及内存地址。在实现细节上，由于 vLLM 采用分页内存管理（PagedAttention），KV 缓存按块分页，Slot Mapping 也需要与分页机制结合，以兼容动态长序列的内存分配和回收。

  • 推理流程调整

    在上下文并行下，推理流程有所不同：预填充阶段，对于长请求，调度器将其标记需使用 PCP 并发，将该请求占用 PCP 组中的所有 GPU 进行并行计算；解码阶段，在每步生成时，DCP 组的 GPU 需要先各自计算局部结果，然后在组内执行一次 All-Reduce 通信合并输出。这些并行计算和通信通过 CUDA 流异步调度，在不阻塞其他请求的前提下完成。vLLM 利用了 CUDA 图（Cuda Graph）和流并行，将通信开销和计算尽量重叠隐藏。例如，在 decode 阶段，同步操作只在必要的点（如 All-Reduce 前后）插入，其余部分与其他流上的计算可并行。调度器还需解决预填充和解码阶段交错执行时的资源竞争—— vLLM 采用解耦架构，预填充工作线程和解码工作线程可以并行，将预填充耗时与解码生成重叠，进一步提高 GPU 利用率。

  • 兼容性与优化

    vLLM 的上下文并行兼容常见的注意力变种如 多查询注意力（Multi-Query Attention）、分组查询注意力（Grouped-Query Attention，GQA） 以及 单头潜在注意力（Multi-Head Latent Attention, MLA） 模型。这些模型有效减少了 KV 头的数量（降低 HH），使得较小的 TP 并行度即可无重复地切分 KV 缓存。但对于极大模型（如数百亿参数以上），TP 往往需要开到远超 HH 才能利用足够 GPU，此时 DCP 依然有用武之地。此外，vLLM 还支持将 DCP 与**多 Token 并行解码（MTP, Multi-Token Prediction）**结合，在生成多个 token 时同时并行多个解码步，以进一步加速长上下文生成。

综上，vLLM通过上下文并行技术，实现了对超长上下文请求的高效支持。在预填充阶段，PCP 大幅缩短了处理长 Prompt 的延迟，优化了用户等待时间；在解码阶段，DCP 突破了单卡 KV 缓存瓶颈，提升了吞吐和并发能力。上下文并行与其它并行手段（数据并行、张量并行等）相结合，为大模型提供了可伸缩的部署方案。对于实际使用者，一般建议：在满足精度前提下尽量提高张量并行以加速前馈计算，然后使用上下文并行来应对 KV 缓存的长序列问题。凭借上下文并行，vLLM 能够在不损失准确性的情况下，服务百千 Token 级上下文的请求并保持实时的响应速度。这一技术创新为长上下文大模型的实用化铺平了道路，使得交互式AI可以在“记忆”海量内容的同时，依然快速地回答用户的每一个问题。

参考链接

  1. [2507.07120] Helix Parallelism: Rethinking Sharding Strategies for Interactive Multi-Million-Token LLM Decoding

    https://ar5iv.labs.arxiv.org/html/2507.07120

  2. [Feature]: Context Parallelism · Issue #7519 · vllm-project/vllm · GitHub

    https://github.com/vllm-project/vllm/issues/7519

  3. Helix: Serving Large Language Models over Heterogeneous GPUs and Network via Max-Flow

    https://arxiv.org/html/2406.01566v2

  4. Context_Parallelism_Presentation

    https://mlsys.org/media/mlsys-2025/Slides/3255.pdf

  5. Context Parallel Deployment - vLLM

    https://docs.vllm.ai/en/latest/serving/context_parallel_deployment/

  6. [RFC]: Support Prefill Context Parallel (PCP) · Issue #25749 · vllm-project/vllm · GitHub

    https://github.com/vllm-project/vllm/issues/25749

  7. block_table - vLLM

    https://docs.vllm.ai/en/latest/api/vllm/v1/worker/gpu/block_table/

  8. [Feature] Implement Decode Context Parallel in SGLang · Issue #12196 · sgl-project/sglang · GitHub

    https://github.com/sgl-project/sglang/issues/12196

  9. [PDF] DCP: Addressing Input Dynamism In Long-Context Training …

    https://www.semanticscholar.org/paper/DCP%3A-Addressing-Input-Dynamism-In-Long-Context-via-Jiang-Cai/5f3dd2fd7b80dad7b73a7d09464ecc078ce12035

  10. [PDF] Learning to Shard: RL for Co-optimizing the Parallelism Degrees …

    https://www.arxiv.org/pdf/2509.00217

Previous
通过零开销逐层权重卸载技术将SGLang Diffusion wan2.2的推理速度加速60%
Next
FlashAttention 原理与实现