学习链接¶
- 图解大模型计算加速系列:FlashAttention V1,从硬件到计算逻辑 - 知乎
- 图解大模型计算加速系列:FlashAttention V2,从原理到并行计算 - 知乎
- Flash Attention 的实现原理
- [Attention优化][2w字]📚原理篇: 从Online-Softmax到FlashAttention V1/V2/V3 - 知乎
- FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning
- flash attention v1-v3系列论文解读[all] - 知乎
- CUDA-MODE课程笔记 第12课,Flash Attention
- Understanding Flash Attention: Writing Triton Kernel Code
- ELI5: FlashAttention. Step by step explanation of how one of… | by Aleksa Gordić | Medium
- CUDA 学习:FlashAttention-2 (Part 1) - 知乎
- Flash Attention深度解析 - 知乎
- Flash Attention 全解析(上):从 V1、V2 到 Flash Decoding 的演进与思想 - 知乎
- Flash Attention 全解析(下):从硬件、算法到指令,榨干 H100 的异步Flash Attention V3 - 知乎
- [Decoding优化]🔥原理&图解FlashDecoding/FlashDecoding++ - 知乎
- FlashAttention V3 论文原理分析 - 知乎
- flash attention的CUDA实现探讨-V3 - 知乎
一、引言:Attention 机制与内存瓶颈背景¶
自 Transformer 提出以来,“自注意力(Self-Attention)”已经成为大型模型的核心组件。其基本公式为:
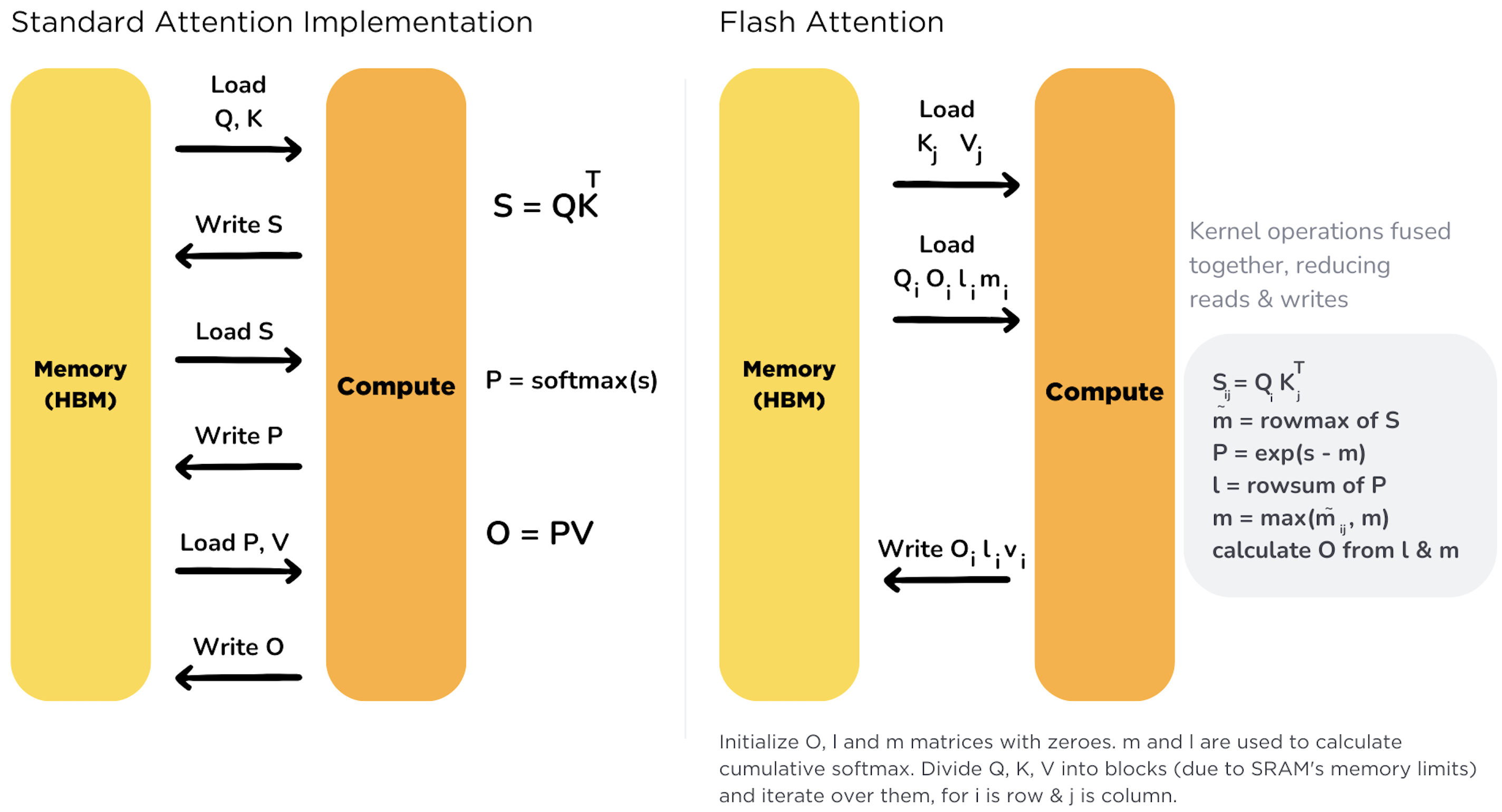
其中 分别是查询、键、值矩阵, 是每个注意力头的维度。这个计算需要先计算 得到 的注意力得分矩阵,再对每一行执行 Softmax 归一化,最后与 相乘得到输出 。如图 1 所示,标准实现中,这三个步骤通常拆分为独立的矩阵运算,会产生大量中间结果。

内存与计算挑战: 注意力的时间和空间复杂度均为 ,当序列长度 增大时,内存占用和数据传输量会呈二次方增长。例如,长度翻倍会导致注意力矩阵元素数量增加四倍。这导致 GPU 上内存访问成为瓶颈——对巨大的 矩阵和 Softmax 中间结果的反复读写使计算受限于内存带宽。事实上,在大模型推理中,尽管 GPU 算力很强,显存的读写速度往往限制了注意力层的性能。
此外,Softmax 计算本身也存在数值稳定问题:直接对大数取指数可能溢出,需要减去最大值来稳定计算,这通常需要多次遍历数据(例如“三遍法”分别计算最大值、指数和归一化)。总的来说,注意力的内存开销和 Softmax 处理成为 Transformer 扩展长序列时亟待解决的瓶颈。
FlashAttention 正是在这种背景下诞生:通过重排计算顺序和融合算子,以 IO(内存访问)优化为核心,使注意力计算的内存占用从二次降到线性,并显著提升实际运行速度。下文将详细介绍 FlashAttention 的各个版本(V1、V2、V3)的算法原理与实现优化。
二、FlashAttention V1:块式算法与 Online Softmax 优化¶
FlashAttention V1(最初发表于 2022 年)是 Tri Dao 等人提出的精确且内存高效的注意力计算算法。它的核心思想是在不引入近似的前提下,通过块式(block-wise)计算和在线 Softmax 技巧,将注意力的中间结果限制在高速缓存中,从而减少显存读写。
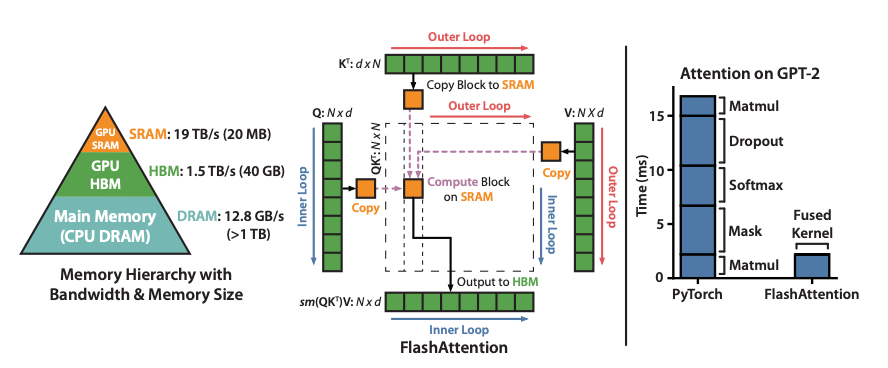
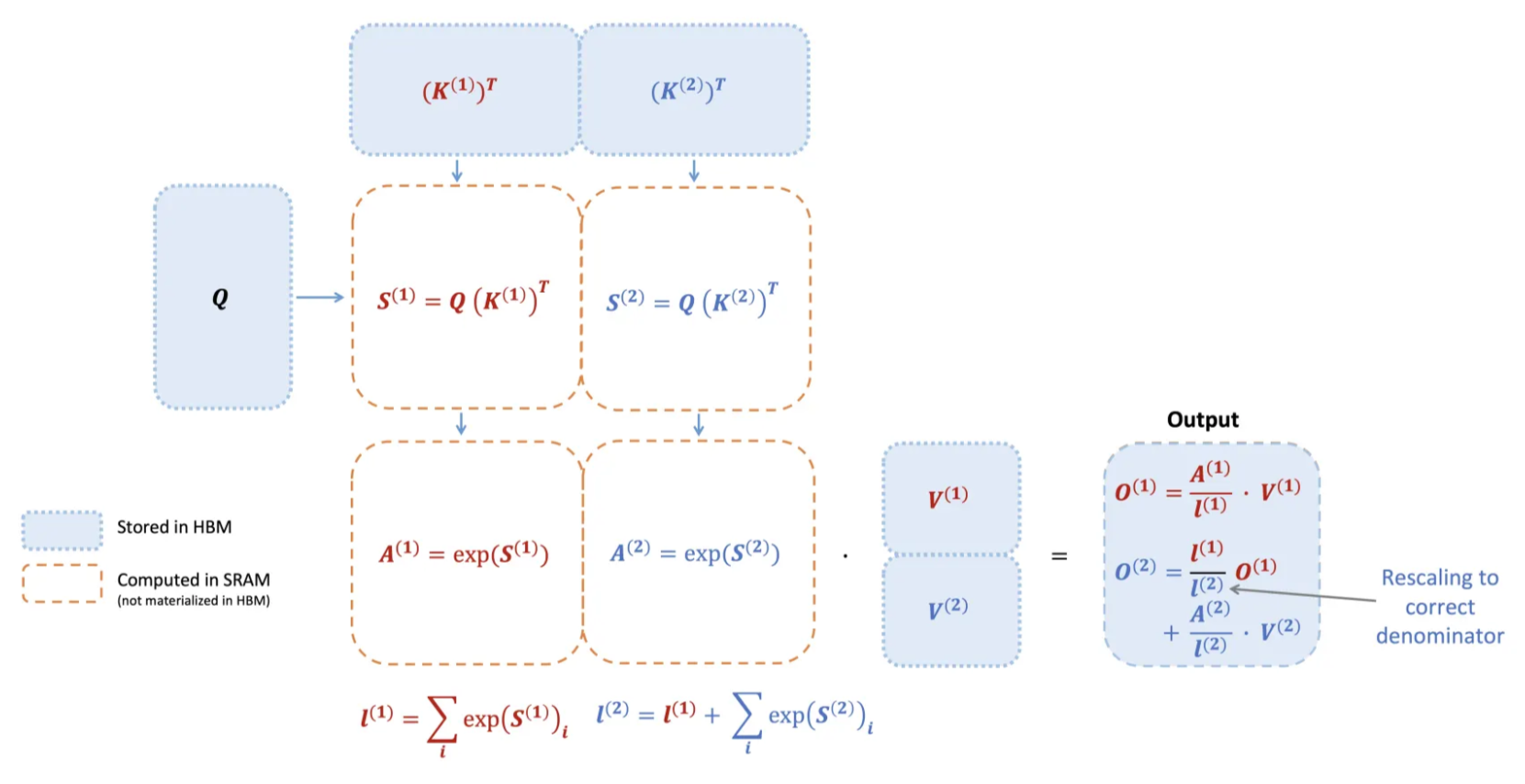
图 2:FlashAttention V1 的块式注意力计算原理示意图。将长序列的 拆分成多个块分批加载至片上高速内存(SRAM)计算,与每个块对应的 批次进行乘积并软最大归一化,再累积输出结果。蓝色框表示存储在 GPU 显存(HBM)的大矩阵未被 materialize,橙色虚线框表示在片上 SRAM 中计算的部分。最终通过重新缩放确保整体 Softmax 正确归一化。
2.1 块式计算与内存优化¶
块式(tiling)计算: FlashAttention 将 划分为适合片上缓存的小块,逐块完成注意力计算。具体而言,算法每次从显存(HBM)加载一块 和对应的 (例如块大小 )到共享内存,然后对这块数据与所有查询 分块进行计算。与传统方法一次性计算整个 不同,FlashAttention 从不在显存中构造完整的 注意力矩阵。取而代之,它在片上 SRAM 中分块计算并及时消耗这些局部结果。例如,假设将 各分成两块:先计算第一块 对输出的贡献,再计算第二块 ,最后将两部分结果正确叠加。由于不写入/读取大中间矩阵,这种分块策略使所需内存读写量从 降至 ,大幅降低了GPU全局内存访问。实践中,这种 IO 优化带来了约 2~4倍 的时间加速。更重要的是,内存占用从二次降为线性,使得长序列(如数万长度)在有限显存中成为可能。
融合与单Kernel实现: FlashAttention 将注意力的多步计算融合进单个 CUDA 核函数。传统实现需要依次启动独立 kernel 计算 、Softmax、,期间中间结果多次写回显存。FlashAttention V1 则通过一个内核完成点积、Softmax 归一化、再乘 的完整流程,并处理必要的 mask 操作。这消除了内核间切换和同步开销,也避免了不同 kernel 之间反复读写显存。这一“kernel 融合”手段结合块式计算,使得注意力的计算完全在片上缓存中进行,大幅减少了慢速 HBM 的访问。总之,FlashAttention V1 充分利用 GPU 内存层次结构(寄存器、共享内存 vs. 全局显存),通过以算代存来提升性能——牺牲一些额外的算术操作来避免昂贵的内存 I/O。
2.2 Online Softmax:把“全行归一化”拆成“逐块可合并”的稳定统计量¶
块式 attention 的最大障碍在 Softmax:对每个 query 行 ,Softmax 需要整行 logits 的 全局最大值与全局指数和:
如果我们把 沿序列维分成多个块(block),那么每次只看到 logits 的一个子向量 。想要不 materialize 全量 ,就必须支持“看到一块就更新一次 Softmax 的归一化信息”。
FlashAttention 的做法是:为每个 query 行维护两类可增量合并的稳定统计量:
- :到目前为止见过的 logits 的运行最大值(running max)
- :到目前为止见过的 logits 的稳定指数和(running exp-sum),也可以理解为 空间的分母,但总是以 的形式存储
这对应经典 log-sum-exp(LSE)稳定形式:
假设我们已经处理完前 个块,得到 。现在处理第 个块,先算它自己的局部统计量:
合并时,新全局最大值就是:
关键在于: 的基准从旧的 切换到了新的 ,所以要对旧的累积指数和做一次“重标定(rescale)”:
这一条就是 Online Softmax 的核心:你不需要保存任何历史 logits,只要保存 ,就能把新的块稳定地合并进去。
2.3 累积输出:把 也做成“可合并”的形式¶
Softmax 的最终输出是:
如果我们只更新分母 还不够,还得更新分子(加权和值)。FlashAttention 做法是维护一个未归一化的累计分子(但同样用稳定基准):
- :到目前为止的稳定加权和(running weighted sum)
对第 块,先算局部未归一化权重:,然后做两件事:
- 把旧的累计分子从基准 切到 (同样 rescale)
- 加上当前块的贡献
写成公式就是:,最终输出在所有块结束后一次性归一化:。
def online_softmax_blocked(Q_block, K, V, Bc):
# Q_block: [Br, d], K: [T, d], V: [T, d]
Br, d = Q_block.shape
m = np.full((Br,), -np.inf, dtype=np.float32) # running max
l = np.zeros((Br,), dtype=np.float32) # running exp-sum
acc = np.zeros((Br, d), dtype=np.float32) # running weighted sum
for start in range(0, K.shape[0], Bc):
K_blk = K[start:start+Bc] # [Bc, d]
V_blk = V[start:start+Bc] # [Bc, d]
S = (Q_block @ K_blk.T) * scale # [Br, Bc]
S = apply_mask_if_needed(S) # causal/pad -> -inf
m_blk = S.max(axis=1) # [Br]
m_new = np.maximum(m, m_blk) # [Br]
# rescale old stats to the new max
exp_m = np.exp(m - m_new) # [Br]
l *= exp_m
acc *= exp_m[:,None]
# add contribution of this block under the new max
P = np.exp(S - m_new[:,None]) # [Br, Bc]
l += P.sum(axis=1) # [Br]
acc += P @ V_blk # [Br, d]
m = m_new
O = acc / l[:,None]
LSE = m + np.log(l)
return O, LSEdef online_softmax_blocked(Q_block, K, V, Bc):
# Q_block: [Br, d], K: [T, d], V: [T, d]
Br, d = Q_block.shape
m = np.full((Br,), -np.inf, dtype=np.float32) # running max
l = np.zeros((Br,), dtype=np.float32) # running exp-sum
acc = np.zeros((Br, d), dtype=np.float32) # running weighted sum
for start in range(0, K.shape[0], Bc):
K_blk = K[start:start+Bc] # [Bc, d]
V_blk = V[start:start+Bc] # [Bc, d]
S = (Q_block @ K_blk.T) * scale # [Br, Bc]
S = apply_mask_if_needed(S) # causal/pad -> -inf
m_blk = S.max(axis=1) # [Br]
m_new = np.maximum(m, m_blk) # [Br]
# rescale old stats to the new max
exp_m = np.exp(m - m_new) # [Br]
l *= exp_m
acc *= exp_m[:,None]
# add contribution of this block under the new max
P = np.exp(S - m_new[:,None]) # [Br, Bc]
l += P.sum(axis=1) # [Br]
acc += P @ V_blk # [Br, d]
m = m_new
O = acc / l[:,None]
LSE = m + np.log(l)
return O, LSE下图展示了分块计算的整体流程:
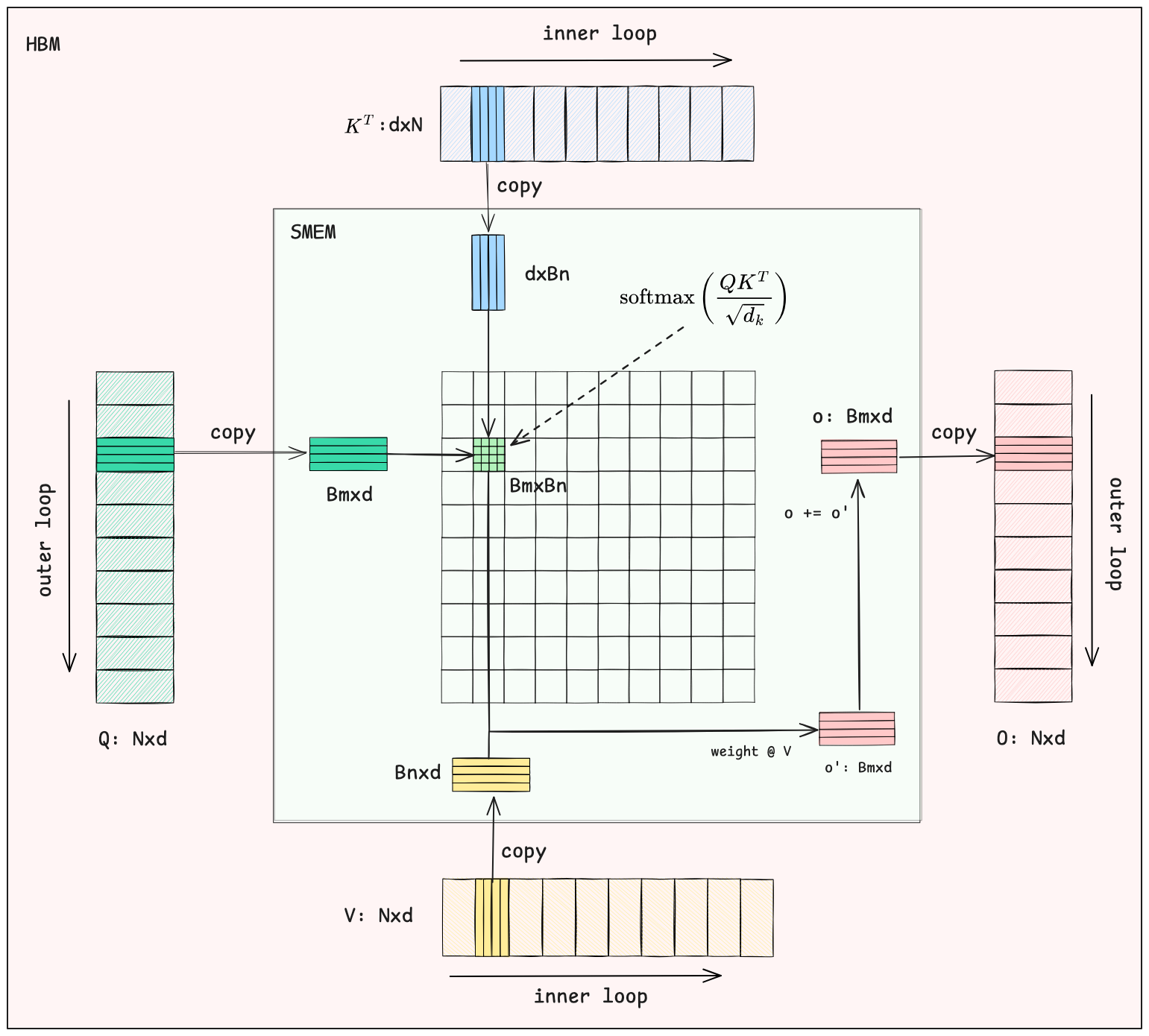
图中, 被划分为多个 的分块, 和 被划分为多个 的分块,计算流程包含两层循环:
-
外层循环
外层循环遍历 矩阵的小块,这里每一个块都包含 个 token,其中每个 token 的维度为 。因为通常使用的是多头注意力机制,每个头的维度通常为 64 到 128 这样的量级,所以这里 通常不会很大, 矩阵的分块可以很容易地加载到共享内存中进行计算。
-
内层循环
内层循环中,每次读取 和 矩阵的小块,这里每一个块都包含 个 token。使用 矩阵的小块与 矩阵的小块计算注意力权重,并使用 online softmax 融合加权求和的方式,计算出当前 矩阵小块对应的输出结果。然后不断将结果累加并修正,直到遍历完所有的 和 矩阵,最后得到完整的输出结果。
三、FlashAttention V2:并行化与 Kernel 设计改进¶
随着模型上下文长度不断攀升(32K 甚至 128K),FlashAttention V1 尽管高效,但仍有进一步优化空间。FlashAttention V2(2023年提出)在保持V1 精确和内存高效特性的基础上,针对 GPU 实现引入了更优的并行策略和工作划分,从而实现近2倍的加速。其主要改进包括:减少非矩阵计算开销、更好地利用 GPU 并行资源,以及改进线程内的工作分配。
3.1 减少非矩阵运算开销¶
现代 GPU 上的 Tensor Core 对矩阵乘法有极高吞吐,而标量操作(除法、指数、比较等)则慢得多。FlashAttention V2 重新梳理了 V1 中的 Softmax 计算,将一些频繁执行的重缩放(rescale)、边界检查和掩码操作等尽量移出主循环或合并,减少了这些非矩阵类 FLOP 的次数。例如,在 Online Softmax 过程中,只在必要时做归一化调整,避免对每块重复做比例缩放。又如将软掩码的检查融入计算流程,尽量利用 GPU 的向量化指令替代显式判断。这些改动虽然不改变算法结果,但节省了很多 GPU 上“慢指令”的开销。据统计,Ampere 架构下一个 FP32 除法/指数等特殊函数的吞吐仅是 Tensor Core 矩阵乘法的 1/16 甚至更低。因此,通过减少这些操作,V2 能让 GPU 更多时间用于高速的矩阵乘法,从而提高整体 FLOPs 利用率。
3.2 跨序列长度的并行¶
FlashAttention V1 的并行化维度主要是批次(batch)和多头(head)。它为每个注意力头启动一个线程块(block),总共启动batch_size * num_heads个线程块并行计算。在典型训练场景(大batch、多头)下,这样可以占满 GPU 的大部分 SM。然而在长序列-小 batch 的推理或训练下,V1 常出现 GPU 资源利用不充分的问题:比如 batch size 很小且序列很长时,线程块数不足以占用全部 SM。V2 针对这一情况,增加了沿序列长度方向的并行。具体做法是在前向计算中,将注意力矩阵按“查询序列”的行拆分,由多个线程块分别处理不同的行块。这样,即使 batch 很小,每个 head 的长序列也能拆分成多个部分并行计算,从而大幅提高 SM 占用率。如图 3 所示,在前向过程中,不同线程块(Worker)各负责注意力矩阵的一部分行;在反向过程中,则各负责一部分列,以避免竞争更新梯度时的冲突。这种沿序列拆分的调度使 FlashAttention 在极长序列、小批量情况下仍能接近满 GPU 并行度,从而支持更长上下文并提升此情形下的速度。
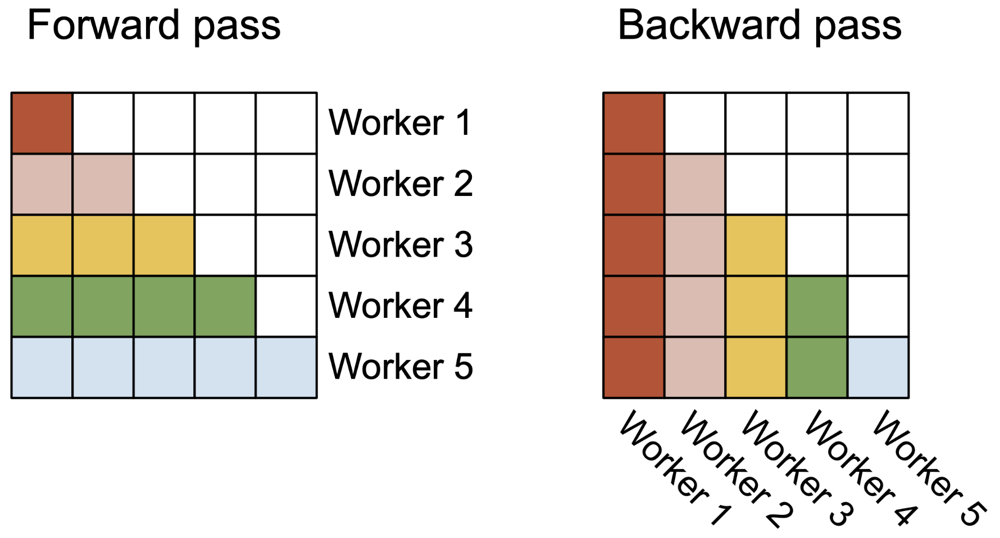
图 3:FlashAttention-2 中跨线程块的并行调度示意。左图为前向传播:每个“Worker”(线程块)负责注意力矩阵的一块行片段,例如 Worker1 处理红色行块,Worker2 处理粉色行块等。右图为反向传播:每个线程块负责一块列片段,例如 Worker1 处理红色列块,Worker2 处理粉色列块等。这种沿序列长度的划分提高了长序列小批量情况下 GPU 的利用率。
3.3 改进线程块内的 Warp 分工¶
在 GPU 上,一个线程块包含若干个 Warp(每个 Warp 32 个线程)。在 FlashAttention V1 中,采用的是“切分 K(split-K)”的方案:即每个 Warp 各自处理一部分 和对应的 ,计算部分的 ,然后需要将各 Warp 的结果写入共享内存并同步,加和得到完整输出。这种方案需要 Warps 间频繁同步和共享内存通信,造成一定开销。FlashAttention V2 改为“切分 Q(split-Q)”方案:让每个 Warp 处理不同的查询 子块,而使所有 Warp 都能访问完整的 和 块。这样,每个 Warp 可以独立完成自己那部分 乘积并直接乘以共享的 得到对应输出片段,无需与其他 Warp 交换中间结果。图 4 展示了两种 Warp 分工方式的对比:FlashAttention-1(左)中不同颜色 Warp 各处理一部分 ,需要写共享内存(圆圈部分)再汇总;FlashAttention-2(右)则每个 Warp 处理不同的 行,避免了 Warp 间通信。这种改进显著减少了片内共享内存的读写和同步屏障,使单个线程块内部执行更高效。
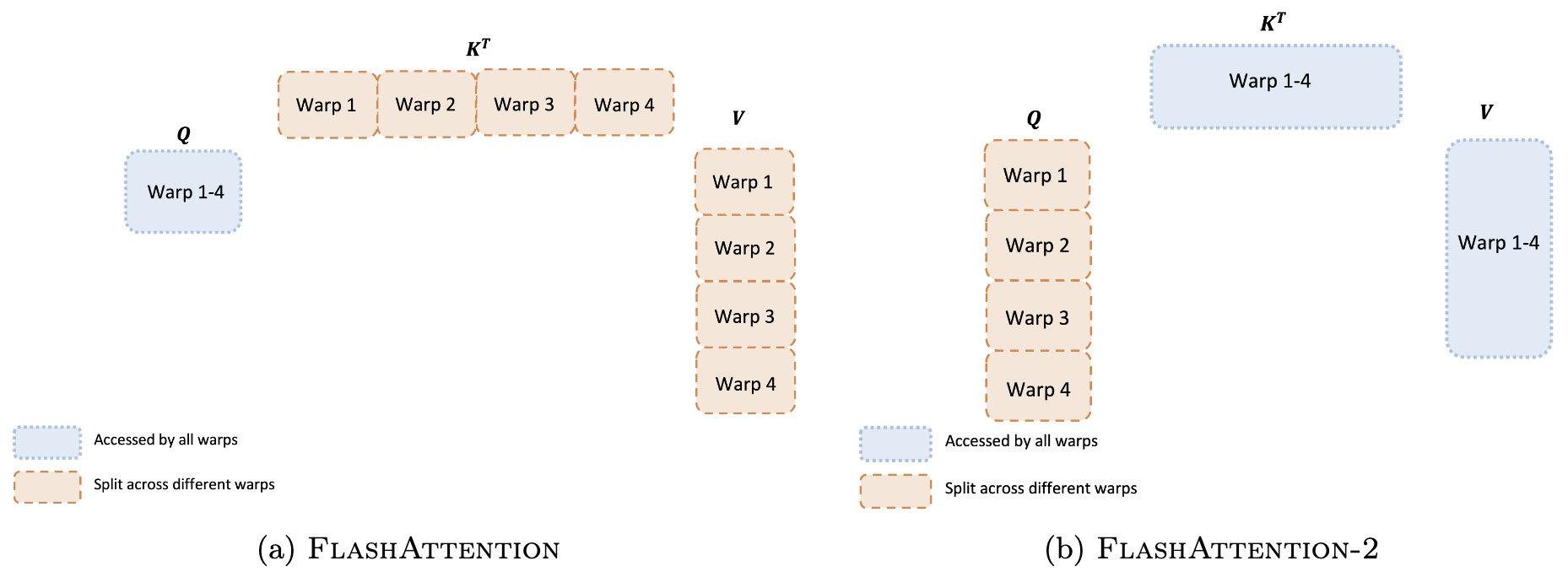
图 4:Warp 级工作划分对比。(左)FlashAttention-1 中采用“切分 K”方案,不同 Warp 处理不同列块(K 块),需要在共享内存同步累加。(右)FlashAttention-2 改为“切分 Q”方案,不同 Warp 处理不同行块(Q 块),各 Warp 直接算出自己负责的输出部分,无需 Warp 间通信。新方案减少了共享内存读写和同步,提升了效率。
3.4 支持更大 Head 维度与多查询注意力¶
FlashAttention V1 限制每个注意力头维度 ,而一些模型使用到 256 维头。V2 通过内存管理优化支持了 head 尺寸扩展到 256。此外,V2 新增对多查询注意力(MQA)和分组查询注意力(GQA)的支持。这些变体在推理时共享 Key/Value 以减少缓存大小,FlashAttention-2 通过调整索引机制实现了对它们的适配,而无需为每个头单独存储完整的 。
实现与性能: FlashAttention-2 基于 NVIDIA 的 CUTLASS 3.x 和 CuTe 库完全重写,实现了高度优化的 CUDA 内核。相较 V1 的定制 CUDA 实现,新版本在寄存器利用和指令级优化上更进一步,并减少了开发复杂度。值得一提的是,社区也有使用 Triton 实现 FlashAttention 的尝试,但 FlashAttention-2 的官方实现性能更胜一筹,可达原 Triton 版本 1.3~2.5 倍速度。综合上述改进,FlashAttention-2 在 A100 GPU 上的前向+后向总速度达到原版的 2 倍左右,FLOPs 利用率提升到理论峰值的 50~73%(约 230 TFLOPs/s,FP16)。在端到端训练 GPT 等模型时,单卡可稳定运行约 225 TFLOPs/s,相当于 72% 的模型 FLOPs 利用率。同时显存占用仍与序列长度线性关系,保持了大幅节省内存的优势。总结来说,FlashAttention-2 通过更佳的并行和更精细的 kernel 设计进一步压榨了 GPU 性能,使得即使在极长序列或硬件升级的场景下,注意力层依然高效。
四、FlashAttention V3:异步流水线与推理优化¶
2024 年,FlashAttention 家族又迎来两项重要进展:FlashAttention-3 针对最新 H100 等硬件引入异步流水线和低精度优化,将训练推理速度再次提升 1.5~2 倍。
NVIDIA Hopper 架构(如 H100 GPU)引入了若干新特性:Warp 级并行 GEMM 指令(WGMMA)、Tensor Memory Accelerator(TMA)以及更高效的 FP8 矩阵运算等。FlashAttention-3 利用这些硬件能力,实现了计算与数据传输的重叠并行以及更低精度下的高准确率,从而在 H100 上将注意力计算的 FLOPs 利用率提高到约 75%(FP16/BF16)甚至 85%(FP8 模式)。
4.1 异步计算与流水线重叠¶
传统注意力计算流程中,矩阵乘法(GEMM)和 Softmax 是串行的:必须先算完所有 得到注意力得分,再计算 Softmax,再乘 。然而在 H100上,GEMM 和 Softmax 两类操作可以并行重叠执行。原因在于它们使用 GPU 上不同的计算单元(Tensor Core vs. 标量单元),例如 H100 的 FP16 Tensor Core 峰值 989 TFLOPs,而执行指数的标量单元仅 ~3.9 TFLOPs,相差达 256 倍。Softmax 尽管 FLOPs 占比不高,但因为速度慢,如果串行执行会占用总时间约一半。理想状况下,我们希望在 Tensor Core 做矩阵乘法的同时,利用其他单元并行计算Softmax。
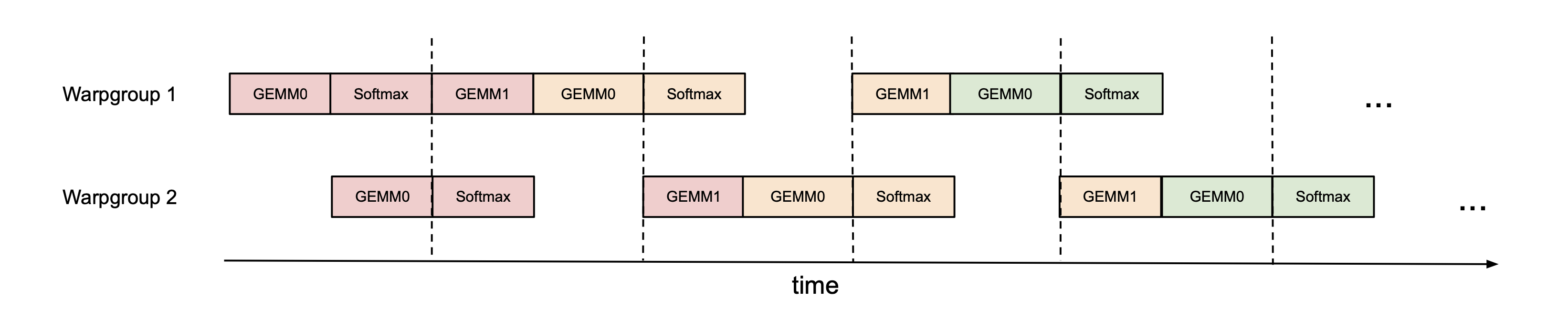
图 5:FlashAttention-3 中跨 Warp 组的 Ping-Pong 异步调度。Warp 组 1(上方)和 Warp 组 2(下方)交替执行矩阵乘 GEMM 和 Softmax 操作:当一组等待矩阵乘结果时,另一组利用空闲执行 Softmax。虚线分隔不同迭代,彩色块表示 GEMM 或 Softmax 所占用的时间段。这样实现两类操作重叠并行,提高了硬件利用率。
FlashAttention-3 通过 Warp 级专业化(warp specialization)实现这一点:将同一线程块内的 Warp 分成两个角色,一部分 Warp 专职执行 GEMM(通过新 WGMMA 指令提高吞吐),另一部分 Warp 专职执行 Softmax 和归一化。然后采用“Ping-Pong 调度”在 Warp 组间交替执行:例如两个 Warp 组,一组先进行当前块的 GEMM 计算,另一组利用这段时间对上一个块执行 Softmax;随后两组交换角色,如此往复。图 5 展示了有两个 Warp 组时的流水线时间表:相同颜色代表同一次迭代,Warp 组 1 先执行 GEMM0 然后 Softmax,而 Warp 组 2 稍后开始 GEMM0,当 Warp 组 1 切换去执行 GEMM1 时,Warp组 2 正好执行 Softmax,以此交错重叠。这种手动的 barrier 调度让两个 Warp 组总有一个在算 Softmax 而另一个在算 GEMM,从而把 Softmax 隐藏在别的计算“阴影”下,提升流水线并行度。实测在 H100 上,FP16 前向算力通过这种 Warp 组 Ping-Pong 调度,速度从 570 TFLOPs 提高到 620 TFLOPs 左右。

除了 Warp 组之间的并行,如图 6 所示,FlashAttention-3 还进一步在单个 Warp 组内实现流水线:将一次 Attention 计算拆成两个阶段,先执行部分 GEMM 累积,再插入 Softmax 计算,然后继续下一个 GEMM。通过在 Warp 内交叉执行,小部分 Softmax 计算可以与本组后续的 GEMM 重叠,从而进一步榨取并行度。这种方案增加了一些寄存器开销(需要同时保存 GEMM 累积和 Softmax 中间值),但换来约 3% 左右额外性能提升(FP16 前向从 620 提升到约 640+ TFLOPs)。
4.2 Hopper 硬件特性利用¶
FlashAttention-3 针对 H100 的新指令做了专门优化。例如使用 WGMMA 指令批量执行 Warp 组矩阵乘法,提高单 Warp 组算力利用;利用 TMA 硬件在后台异步搬运数据块,从 HBM 到共享内存,隐藏内存延迟。通过这些手段,在不增加显式同步的情况下,实现了计算和传输高度重叠。另外,FlashAttention-3 使用 NVIDIA 提供的 CUTLASS 库的抽象封装这些操作,加快开发同时保障性能。这些低级优化共同使得FlashAttention-3 在 H100 上达到了接近峰值的性能:FP16/BF16 模式下前向最高约 740 TFLOPs(75% 理论峰值),比 FlashAttention-2 在 A100 上的 124 TFLOPs 大幅提升;使用 FP8 精度时则进一步达到 1.2 PFLOPs 的惊人水平。
4.3 低精度 FP8 与数值优化¶
除了速度,FlashAttention-3 还探索了更低精度计算以提高效率。FP8 精度下 Tensor Core 吞吐可翻倍,但直接将注意力降到 FP8 会引入较大数值误差。模型激活常出现“outlier”离群值,用低位表示会造成严重量化误差。为此,FlashAttention-3 引入了失相干处理(incoherent processing)技术:对 每个 head 乘以一个随机正交矩阵(如 Hadamard 变换),将少数大值“扩散”到各维度。这样做可降低量化误差,而且 Hadamard 变换本身是线性操作,可以与其他操作(如 RoPE 位置编码)融合而几乎无额外代价。实验表明,对于模拟含 0.1% 大幅值的输入,失相干处理将 FP8 量化误差降低了2.6倍。借助对 outlier 的特殊处理,FlashAttention-3 在 FP8 模式下达到与 FP16 几乎相当的准确率损失:RMSE 误差仅为普通 FP8 实现的约 1/2.6。因此,FlashAttention-3 在不牺牲准确率的前提下成功利用 FP8 把速度再次提升约 1.3 倍。
综合来说,FlashAttention-3 针对新硬件的异步并行和低精度技巧实现了显著性能突破。在 H100 上,其 FP16 推理和训练速度比 FlashAttention-2 提高约 1.5~2 倍,达到 ~75% 理论 FLOPs 利用;FP8 模式下更是达到了近 1.2 PFLOPs 的前所未有速度。这些优化证明:充分发掘硬件并行特性和结合算法创新,仍能在 Transformer 这样成熟的算子上取得大幅改进。这也为未来进一步优化 LLM 推理、以及在其它硬件上移植类似技术指明了方向。
五、Flash-Decoding:自回归长序列解码的并行优化¶
上述 FlashAttention 系列主要针对训练场景的长序列优化。然而在推理/解码阶段,Transformer 通常是自回归地一个一个地生成 token,每次只计算一步注意力。典型情况下,解码时当前查询长度为 1(即每次只生成一个新 token),但需要和前面可能数千甚至数万长度的上下文计算注意力。这一特点导致原版 FlashAttention 在推理时遇到新的性能挑战:
- 低并行度问题: 自回归解码时每次只有一个查询向量,FlashAttention V1/V2 将线程块并行在查询长度和 batch 上。如果 batch size 也很小(常见于单句生成),那么 GPU 的大部分 SM 在计算一个注意力头时都是闲置的(例如 A100 有 108 个SM,而 batch=1 时 FlashAttention 只用到 1 个 SM 不到)。即使序列很长, 很多,V1/V2 也只能在一两个 SM 上顺序分块处理,GPU 利用率极低。
- 注意力仍是主要瓶颈: 在推理阶段,Transformer 的其余计算(前馈网络等)可以缓存和批处理,但注意力的计算量随上下文长度增长。特别是当支持超长上下文(数万 token)时,注意力占据生成过程的大部分时间。为提升吞吐,必须针对这种“一对多”的特殊情况优化注意力 kernel。
为此,Tri Dao 等人提出了 Flash-Decoding 技术。它借鉴 FlashAttention 的思路,但新增沿 KV 长度的并行来充分利用 GPU,即对键/值序列进行拆分并行处理。核心思想如下:
- 切分 KV 缓存:将全部过往 Tokens 的键、值 矩阵按序列长度方向分割成若干较小的块(chunk)。例如总长度 分成 个 chunk,每个大小约 。这些块仅是对原 在内存中的视图,不需要真实拷贝。
- 并行计算局部注意力:为每个 chunk 启动一个 FlashAttention 内核,计算当前查询与该 chunk 的注意力输出部分 ,同时计算该 chunk 局部的 值(对应 Softmax 分母的一部分)并存储。这一步相当于并行执行多次“查询与子序列”的注意力,产生各自归一化的局部结果和一个缩放系数。
- 跨块归并输出:在上述并行计算完成后,再启动一个小 kernel 将各 chunk 的部分输出 合并成完整输出 。合并时利用每个 chunk 提供的 信息,按概率正确加权叠加各部分。这相当于执行一次全局 Softmax 归一化:把各块之前局部 Softmax 得到的值按照它们占全局分母的比例进行缩放和累加。
通过上述过程,Flash-Decoding 实现了两级在线 Softmax:每个 chunk 内部用了 FlashAttention 的在线算法计算局部 Softmax,chunk 之间再通过一次归并完成全局 Softmax。关键在于,第二步的多 kernel 完全并行使得 GPU 所有 SM 都被利用来处理不同段的 。只要上下文长度足够大划分出足够 chunk,即使 batch=1,GPU 也可以满载运行注意力计算。这使得推理时注意力耗时基本只随显存带宽线性增长,而不像以前随序列长度急剧恶化。
实验显示,在如 Code Llama-34B 等模型上,Flash-Decoding 对长序列(比如 64k tokens)推理速度有量级提升:与标准 PyTorch 或 FasterTransformer 等方案相比,长上下文下吞吐最高提升可达 8 倍。并且它几乎实现了“横向扩展”:序列长度从 512 增加到 64k,Flash-Decoding 方案的生成速度几乎不受影响,而传统注意力方法速度随长度显著下降。值得强调的是,这种加速完全不影响输出结果,仍然是精确的注意力计算,只是巧妙利用了并行资源。Flash-Decoding 已集成进 FlashAttention 库的推理接口(v2.2 版起),为长上下文模型的实际部署提供了实用方案。
六、FlashDecoding++:进一步降低生成延迟的优化¶
在 Flash-Decoding 基础上,学界又提出了 FlashDecoding++(MLSys 2024),该工作由清华大学等团队完成,着重优化了推理延迟和跨硬件适配。FlashDecoding++ 在保持 Flash-Decoding 并行框架的同时,引入三项新技术:
- 异步 Softmax 管线(Asynchronized Softmax)与统一最大值: 针对 Flash-Decoding 归并各 chunk Softmax 时需要同步等待的问题,FlashDecoding++ 提出统一最大值技巧,消除不同部分 Softmax 在归一化时的同步依赖。通过在各部分 Softmax 时引用同一个全局最大值来调整,Softmax 计算可以更早进行流水,减少阻塞。配合细粒度流水线调度,作者报告在预填充阶段加速1.18×,解码阶段加速1.14×。
- 平坦 GEMM 优化与双缓冲: 生成过程中,小批量时会出现很多不同形状的小矩阵乘(如维度不匹配的 、以及一列一列增大的投影矩阵等),这些非均匀 GEMM 难以被统一优化。FlashDecoding++ 分析了这些 GEMM 瓶颈,引入双缓冲(double buffering)等技术,使得 GPU 在执行一个 GEMM 时预取下一个,隐藏内存延迟。针对某些“扁平”大矩阵乘(flat GEMM)的特殊优化带来了高达 52% 的 GEMM 加速。
- 启发式数据流调度: 考虑不同硬件(如 NVIDIA Tensor Core vs AMD 矩阵核心)和不同输入特征下,静态统一的数据流未必最优。FlashDecoding++ 通过启发式策略自适应选择计算走向:例如对小矩阵选用标量核心执行、对大矩阵用 Tensor Core,或对不同 batch /长度采用不同并行度。这种硬件资源自适应的数据流让各种场景下都接近最优,作者报告相比固定策略最多提升 29% 速度。
综合以上优化,FlashDecoding++ 展现出显著的端到端性能提升:在 NVIDIA A100 和 AMD MI210 上对主流 LLM 模型推理实现了平均 1.37× 速度提升。尤其在首token延迟和流式生成每个 token 延迟上,FlashDecoding++ 均领先。
七、总结:FlashAttention 演进路径与应用场景¶
从 FlashAttention V1 到 V3,以及针对推理的 Flash-Decoding 系列,注意力加速技术完成了从 IO 优化到并行极限、从通用训练到专门推理的逐步演进:
- FlashAttention V1 聚焦于算法重组和内存层次优化,通过块式计算和在线 Softmax 使注意力计算在 GPU 上更加“IO 友好”,实现了注意力精确计算的首次大幅加速。它适用于几乎所有 Transformer 注意力计算场景,大幅降低了显存占用并提升训练速度,已经成为众多开源模型的默认实现。
- FlashAttention V2 在 V1 基础上深入 GPU 并行架构优化,解决了长序列小批量时的扩展性问题,引入跨序列并行和 warp 级无同步分工,实现了接近硬件上限的效率。它使得超长上下文训练成为可能(例如 2 倍序列长度下仍可高效训练),并在 A100 上达到了与 GEMM 相当级别的高利用。V2 适用于训练和推理中序列长度极长但需要充分利用硬件的情况。
- FlashAttention V3 利用新硬件特性(如 H100 的异步 Tensor Core、FP8)将注意力计算推进到流水线并行的新阶段,显著提升了 Hopper GPU 上的性能上限。通过异步重叠计算和低精度优化,V3 为下一代硬件上的 LLM 训练和推理奠定了基础。其 Warp 级流水线思想也可为其他 GPU 程序优化提供思路。
- Flash-Decoding 系列专门面向自回归推理这一新挑战,通过并行化 attention 计算和一系列 pipeline 改进,将长上下文生成的端到端延迟显著降低。Flash-Decoding 让长度从几千提升到数万时的推理成本不再高不可攀,对于需要长文档处理、对话持续上下文等应用非常关键。而 FlashDecoding++ 进一步优化了单步延迟和跨硬件性能,在工业部署中具有吸引力。
总之,FlashAttention 从 V1 到 V3,以及针对解码的扩展,一步步攻克了 Transformer 注意力在存储、并行、延迟上的瓶颈,成为 Transformer 加速领域的重要里程碑。对于工程实践者来说,这些算法既提供了开箱即用的性能提升,也展现了贴合硬件特性进行深度优化的范例。在未来,我们有理由期待这些思路进一步推广到更多模型组件和硬件平台,继续突破大模型训练与推理的效率极限。
参考链接¶
- From Online Softmax to FlashAttention
- Online Softmax to Flash Attention — and Why it Matters | by Matthew Gunton | Data Science Collective | Medium
- FlashAttention 2: making Transformers 800% faster w/o approximation - with Tri Dao of Together AI
- FlashAttention by hand - DEV Community
- Aman’s AI Journal • Primers • FlashAttention
- FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision | Tri Dao
- Flash-Decoding for long-context inference
- FlashDecoding++: Faster Large Language Model Inference with Asynchronization, Flat GEMM Optimization, and Heuristics