How To Write A Fast Matrix Multiplication From Scratch With Tensor Cores

发布于 2024-08-10

23070 字

52 min read

标签： CUDA

📝 转载 / 引用来源：作者 Alex Armbruster · 查看原文

如何从零开始使用张量核心编写快速矩阵乘法¶

引言¶

这篇文章详细介绍了我在 NVIDIA Tesla T4 GPU 上使用 CUDA 和张量核心编写优化矩阵乘法内核的最新努力。目标是尽可能快地计算 D=α∗A∗B+β∗C。在这个方程中，D、A、B 和 C 是充满半精度浮点数的大型矩阵，α和β是常数。这个问题通常被称为Half-precision Generalized Matrix Multiply，或简称HGEMM。

张量核心是 NVIDIA 芯片上的专用硬件单元，用于在硬件中实现小型矩阵乘法。我最近对张量核心感兴趣有两个原因。首先，似乎大多数生成式 AI 训练和推理这些天都在 A100 和 H100 上进行。其次，所有这些训练和推理几乎肯定都在这些设备的张量核心上运行，因为它们为矩阵数学提供了与不使用它们相比的巨大吞吐量提升。从这里

来看：H100 GPU 具有 989 TFLOPs 的半精度矩阵乘法计算能力，以及约 60 TFLOPs 的“其他一切”计算能力。因此，张量核心使用的每个周期，你至少获得硬件 94%的利用率。而张量核心未使用的每个周期，你最多获得硬件 6%的利用率。

鉴于它们在当今世界的巨大重要性，当我开始这个项目时，我感觉互联网上关于如何直接使用它们的信息和讨论不成比例地少。我很快了解到，互联网上缺乏讨论可能是因为编写使用它们的算法是一个有点小众的兴趣。调用它们的基本机制并不难，然而编写一个能够接近其全部潜力使用它们的内核是困难的。它们巨大的吞吐量意味着，为了接近其全部潜力使用它们，你需要以最高效的方式通过 GPU 的内存层次移动字节，并将计算与这种数据移动重叠。如果你想从张量核心中获得物有所值，需要使用某些算法技术，本文是对这些技术的探索。

我主要通过挖掘 NVIDIA 的CUTLASS论坛和源代码来弄清楚实现细节，我写这篇文章是为了确保我真正理解自己在做什么，也希望一些试图使用张量核心的 GPU 极客可能会觉得它有帮助。需要注意的是，整个项目是在图灵架构 GPU 上完成的，该架构在 2018 年是最先进的，本文讨论的一些优化细节在一定程度上特定于图灵架构。我在工作中注意到，更现代的 Hopper 架构具有专用硬件支持，直接解决了我针对较旧 GPU 进行优化时遇到的一些性能问题和瓶颈。更现代的 GPU 不仅通过增加的浮点吞吐量来证明其更高的价格标签，还通过减轻试图为其优化内核的程序员的认知负担的功能来证明。

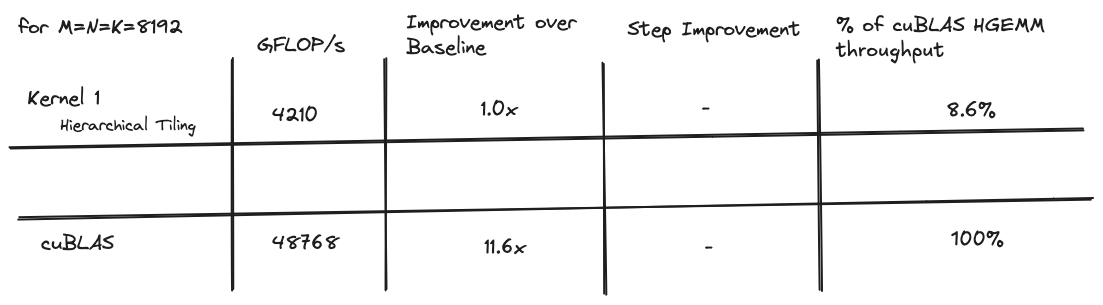
当我开始时，我的目标是编写一个性能与 cuBLAS 的hgemm实现相当的内核，这是 NVIDIA 发布的闭源黄金标准实现。我迭代优化了一系列 6 个内核，其中第一个仅达到 cuBLAS 吞吐量的 8%，而最后一个对于 8192x8192 矩阵达到了 cuBLAS 吞吐量的 96%。

本文包含一个背景部分，解释了在思考如何优化矩阵操作内核时有帮助的一些理论。文章的其余部分解释了我用来使内核尽可能快运行的六种算法技术。代码可以在这里的 github 上找到，这里是一个黑客新闻线程，你可以在那里留下评论。

以下是所有内核的性能比较表格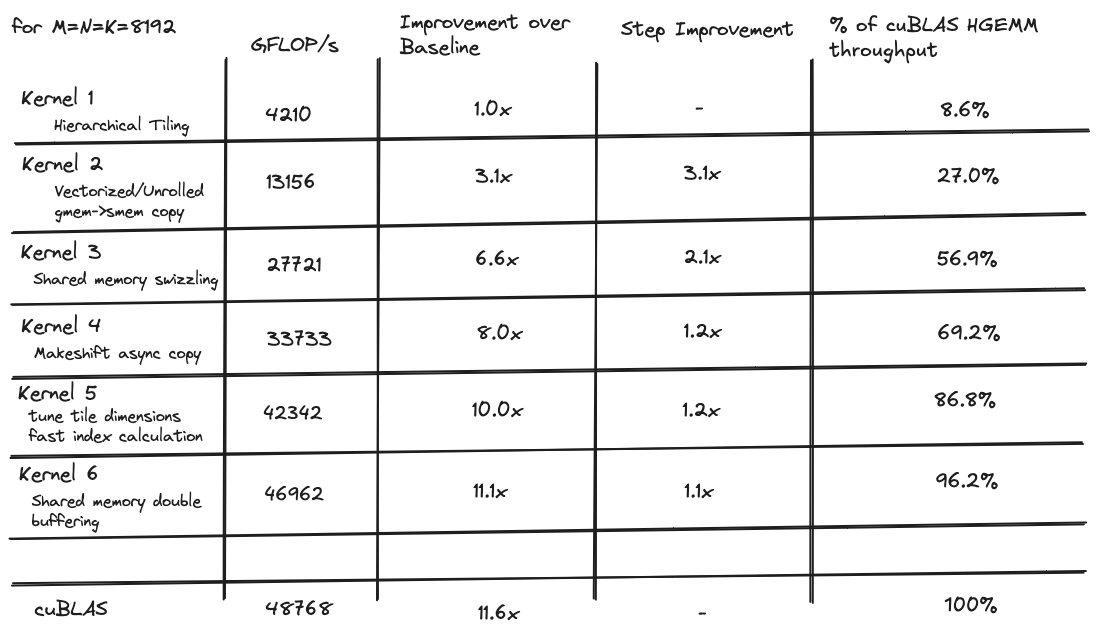： table6

背景¶

内存墙¶

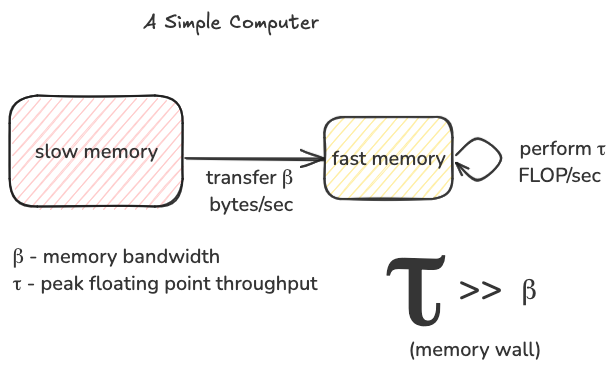
在人类开始建造基于晶体管的计算机以来的大约 70 年里，执行算术的能力一直沿着摩尔定律指数增长，而将数据从存储位置移动到计算位置的能力并未呈指数增长。这个问题被称为内存墙，它是当今计算机架构中的核心问题之一，尤其当涉及到深度学习工作负载时，尤其是张量核心算法。这对我们来说意味着，如果我们想要利用张量核心每秒约 65 万亿次浮点运算的能力，从 DRAM 每秒移动相应数量的字节可能是一个挑战。

屋顶线图¶

屋顶线模型允许我们更精确地思考这个难题。基本思想是，我们想象一个简化的计算机，具有两级内存层次结构：快速内存和慢速内存。我们只能对驻留在快速内存中的数据进行计算，峰值速率为τ FLOP/秒。慢速内存具有无限大小，并且可以以β字节/秒的速度将数据移动到快速内存中。由于内存墙，τ远大于β。任何给定的计算都有一定数量的浮点运算需要执行，例如，要将一个 M×K 矩阵与一个 K×N 矩阵相乘，我们需要执行 2∗M∗N∗K 次浮点运算。我们的算法每秒能实现的浮点运算次数越多，矩阵乘法的完成速度就越快。屋顶线模型给出了我们每秒可实现的浮点运算次数的上限，受限于τ和β，这些是我们硬件的固定属性。我们将实现的每秒浮点运算次数称为吞吐量 T，T 的上限称为 Tmax。

simple_computer

我们可实现的每秒最大浮点运算次数（Tmax）被建模为一个称为

计算强度或简称 I 的变量的函数，这是我们编写的算法的属性。这个指标以 FLOP/字节为单位衡量我们算法的“数据重用”：对于从慢速内存移动到快速内存的每个字节，我们对其执行多少次浮点运算。根据屋顶线模型，如果你是一个算法设计师，你的主要关注点是编写一个具有高计算强度的算法，换句话说，最大化 I。在实践中，这意味着将一块数据从慢速内存移动到快速内存，然后根据你编写的任何算法，在其上执行尽可能多的有用操作。在快速内存中重用数据对性能很重要，因为我们的内存带宽β有限；与τ相比，它是一个较小的数字，这意味着将这块数据从慢速内存传输到快速内存的成本很高。我们通过在其上执行尽可能多的有用浮点运算来充分利用它。屋顶线模型说，我们可实现的每秒浮点运算次数上限（Tmax）是我们计算强度乘以内存带宽与硬件峰值浮点吞吐量中的较小值。

Tmax=min(β∗I,τ)

这个模型说明 Tmax 可能以两种方式受限：

Tmax 永远不会超过τ。即使我们对移动到快速内存的每个字节执行无限次操作，我们仍然受限于硬件的峰值浮点吞吐量。τ通常是一个非常大的数字，例如对于 T4 GPU，τ等于 65,000,000,000,000 FLOP/秒。如果τ是我们的限制因素，我们处于良好状态，这种情况被称为

计算受限。然而，Tmax 也可能受设备内存带宽乘以算法计算强度的限制。如果τ是无限的，实现的浮点吞吐量将简单地是每秒移动到快速内存的字节数乘以每个移动字节执行的浮点运算次数，即β∗I（注意当你乘以β∗I 时，单位抵消得到 FLOP/秒）。如果β∗I 小于τ，这一项成为 Tmax 的限制因素，这种情况被称为
内存受限。在这种情况下要做的是重写你的算法以增加 I，希望你的算法变得计算受限。这是整个情况的图示，注意我们如何通过改变 I 从内存受限变为计算受限：

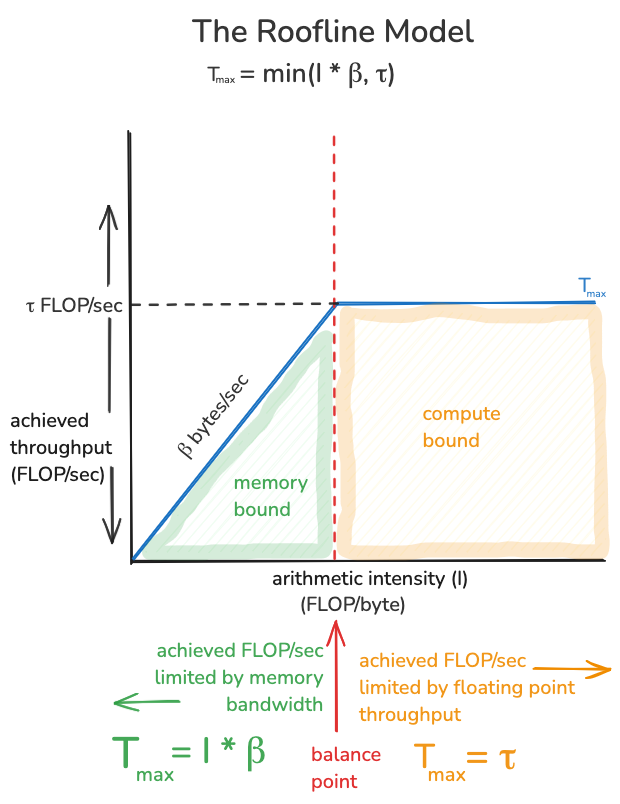
roofline

这张图中的红色虚线被称为硬件的”平衡点”，它是以 FLOP/字节为单位的算术强度水平，我们需要超过这个水平才能从内存受限变为计算受限。如果我们称这个值为 I∗，那么 I∗∗β=τ或等价地 I∗=τβ。它是特定计算机的一个属性，即峰值浮点吞吐量除以内存带宽。由于摩尔定律，算术吞吐量的提高速度远远快于内存带宽，其结果是，一般来说，计算机越新，平衡点越高。

NVIDIA Tesla T4 的屋顶线图¶

将我们使用的 GPU 的一些具体数字代入，并查看得到的屋顶线图，可以指导我们的算法设计，并让我们了解将要面对的情况。在真实的计算机上，不仅仅有一个τ和β，有多个硬件指令，每个指令都有不同的峰值吞吐量τ，还有不同类型的内存，每种内存都有不同的带宽β。

张量核心 vs. FFMA¶

首先，我们需要知道我们设备的全局内存带宽βgmem。NVIDIA 规格表报告

理论内存带宽，这在实践中永远无法实现。实际数字可以通过基准测试找到，根据这篇白皮书，T4 的可实现内存带宽为 220 GB/秒（这是 320 GB/秒理论内存带宽的 68%）。接下来，我们需要知道使用张量核心的峰值浮点吞吐量，以及不使用它的峰值浮点吞吐量。类似于内存，理论数字

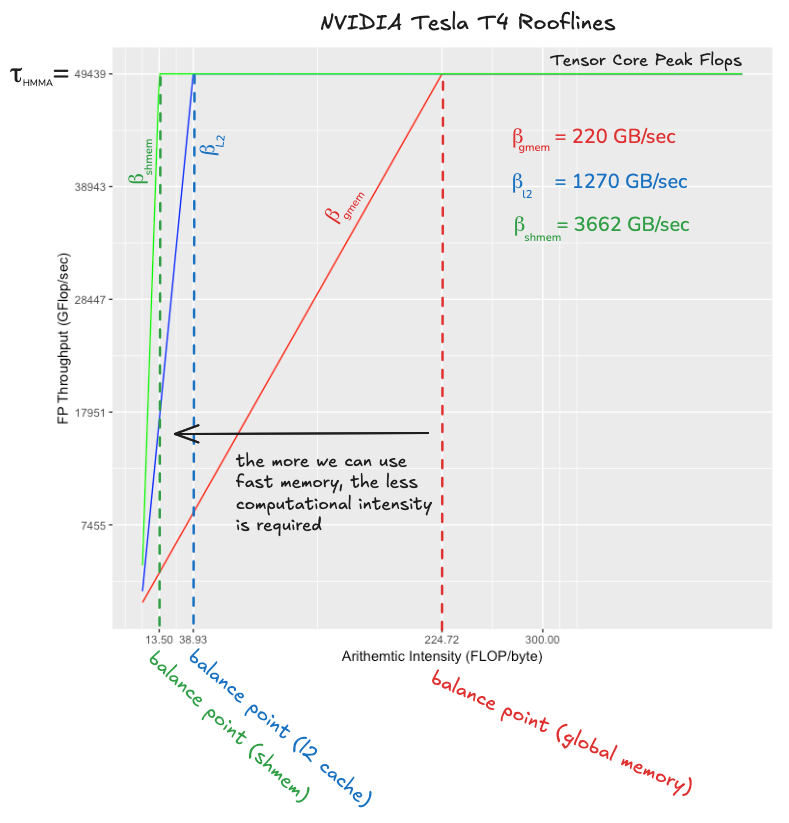
实际上无法实现not actually achievable而无需 GPU 着火或熔化。我认为使用 cuBLAS 半精度（使用张量核心）和单精度（不使用张量核心）GEMM 内核的实测吞吐量作为可实现的浮点吞吐量数字是合理的。查看 cuBLAS 半精度内核的汇编代码，我们可以看到繁重的工作是由HMMA.1688完成的，该指令执行一次小型硬件加速矩阵乘法（稍后详述）。对于单精度 GEMM 内核，执行工作的指令称为FFMA，这是一个标量乘加操作，d=a∗b+c。根据我的基准测试，张量核心 HMMA.1688 的吞吐量为 49439 GFLOP/秒，我们称之为τHMMA。非张量核心 FFMA 的吞吐量为 7455 GFLOP/秒，我们称之为τFFMA。这些分别是理论峰值吞吐量的 76%和 92%，看起来足够合理。由此得到的屋顶线图如下所示（这些图通常以对数/对数比例显示，但此图不是）：

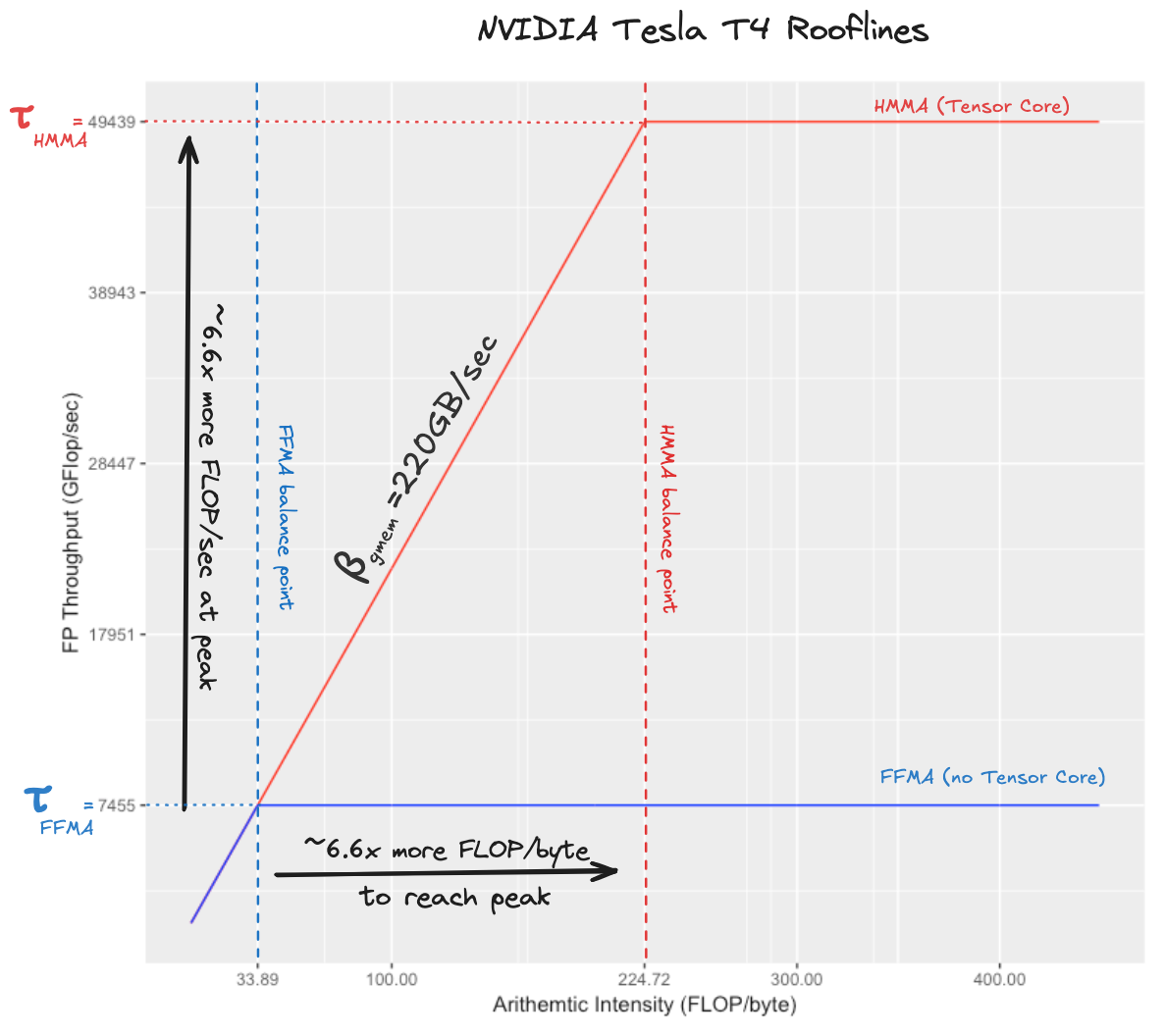
t4_roofline

这个图应该能让我们直观地理解编写一个使用张量核心指令达到峰值 FLOP/秒的内核与编写一个使用融合乘加指令达到峰值 FLOP/秒的内核的相对难度。难度在于，如果我们想达到τHMMA 的吞吐量，我们需要比目标为τFFMA 时高出约 6.6 倍的算术强度。图中的两个平衡点告诉我们，使用 FFMA 指令，我们可以在一个字节从全局内存传输的时间内执行约 33 次 FLOP，而使用张量核心，我们可以在相同时间内执行 224 次 FLOP。这意味着，如果我们有一个使用 FFMA 指令达到峰值 FLOP 的内核，仅仅将内循环中的融合乘加替换为张量核心指令将不足以获得高的张量核心利用率。我们还需要改进数据移动代码，将计算强度提高六倍。这正是编写张量核心 GEMM 有趣的地方之一！

共享内存 vs. L2 缓存 vs. 全局内存¶

如果我们想编写一个能充分利用张量核心的内核，我们需要意识到计算机的内存层次结构。屋顶线模型将内存层次结构简化为两种存储类型：一种大而慢，另一种快而瞬时。实际上，存在多个层级，每个层级具有不同的带宽和容量，并且需要考虑不同的因素以实现高效访问。

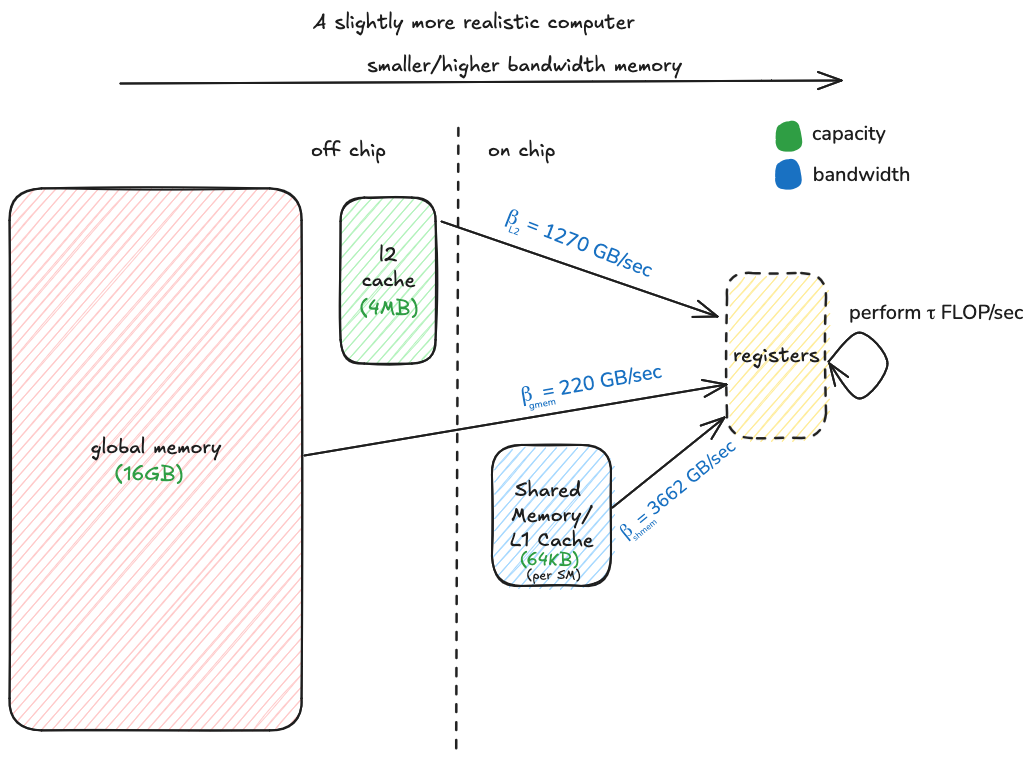
t4_memory_hierarchy

在内存墙的时代，有效利用更快、更小的内存层级至关重要。这需要一些巧思，因为其容量小：例如，在 T4 上，片上共享内存的带宽是全局内存的 16.6 倍，但在单个流式多处理器（简称 SM）上，它只能容纳 64 KiB。如果我们正在乘大矩阵，这仅够容纳问题的一小部分。

t4_memory_roofline

该图比较了张量核心相对于以下层级的平衡点：

全局内存或 DRAM，内存层次结构中最大且最慢的层级
L2 缓存，存储最近从 DRAM 访问的数据，并在 T4 的 16 个 SM 之间共享
共享内存，每个 SM 的快速内存，需要显式管理。

全局内存的平衡点为 224，这意味着如果所有内存访问都指向 DRAM，我们需要为从 DRAM 读取的每个字节执行 224 次 FLOP，以保持张量核心忙碌。事实证明，这是一个非常高的要求，稍后当我们计算算法参数如何影响平衡点时会看到（预览一下：考虑到 T4 上的快速内存量和其他性能因素，实现这个平衡点可能适得其反）。然而，L2 缓存来救援了，它相对于张量核心的平衡点是 38，这是一个更易管理的数字。如果我们的内存访问中有相当一部分能命中 L2 缓存，而不是全部去全局内存，我们就有很大机会成为计算受限而非内存受限。这个故事的寓意是：我们需要 L2 缓存。

共享内存用作显式管理的缓存，用于存储特定 SM（SM 类似于单个 CPU 核心）本地输入矩阵的小部分。在 SM 内部，线程将从共享内存加载问题的本地部分到寄存器内存，数据必须驻留在寄存器中才能进行计算。当共享内存以全带宽运行时，它相对于张量核心的平衡点是 13，这意味着我们需要在寄存器中缓存足够的数据，以便为从共享内存读取的每个字节执行 13 次 FLOP。事实证明，每个 SM 有足够的寄存器内存来轻松实现这一点。当我们优化算法的这一部分时，挑战在于使共享内存能够以全带宽运行，这实际上意味着以无存储体冲突的方式组织数据布局。一旦共享内存达到全带宽，足够的算术强度将易于实现。我认为共享内存平衡点 13 值得注意，因为它告诉我们仅靠共享内存不足以实现峰值张量核心吞吐量。这个故事的寓意是：我们需要寄存器。

理论算术强度¶

因此，现代计算机通常在算术吞吐量和内存带宽之间存在不平衡，因此相对于数据移动执行大量算术的内核能更好地利用硬件。此时，我们需要考虑我们正在运行的算法，暂时忘记硬件。

矩阵乘法 vs 矩阵加法¶

任何给定算法都有一个可能的最大算术强度，作为算法设计者，我们的目标是编写一个内核，使其算术强度尽可能接近这个上限。比较两个 N×N 矩阵相加与相乘时可实现的最大算术强度，说明了不同算法在这方面有不同的上限。

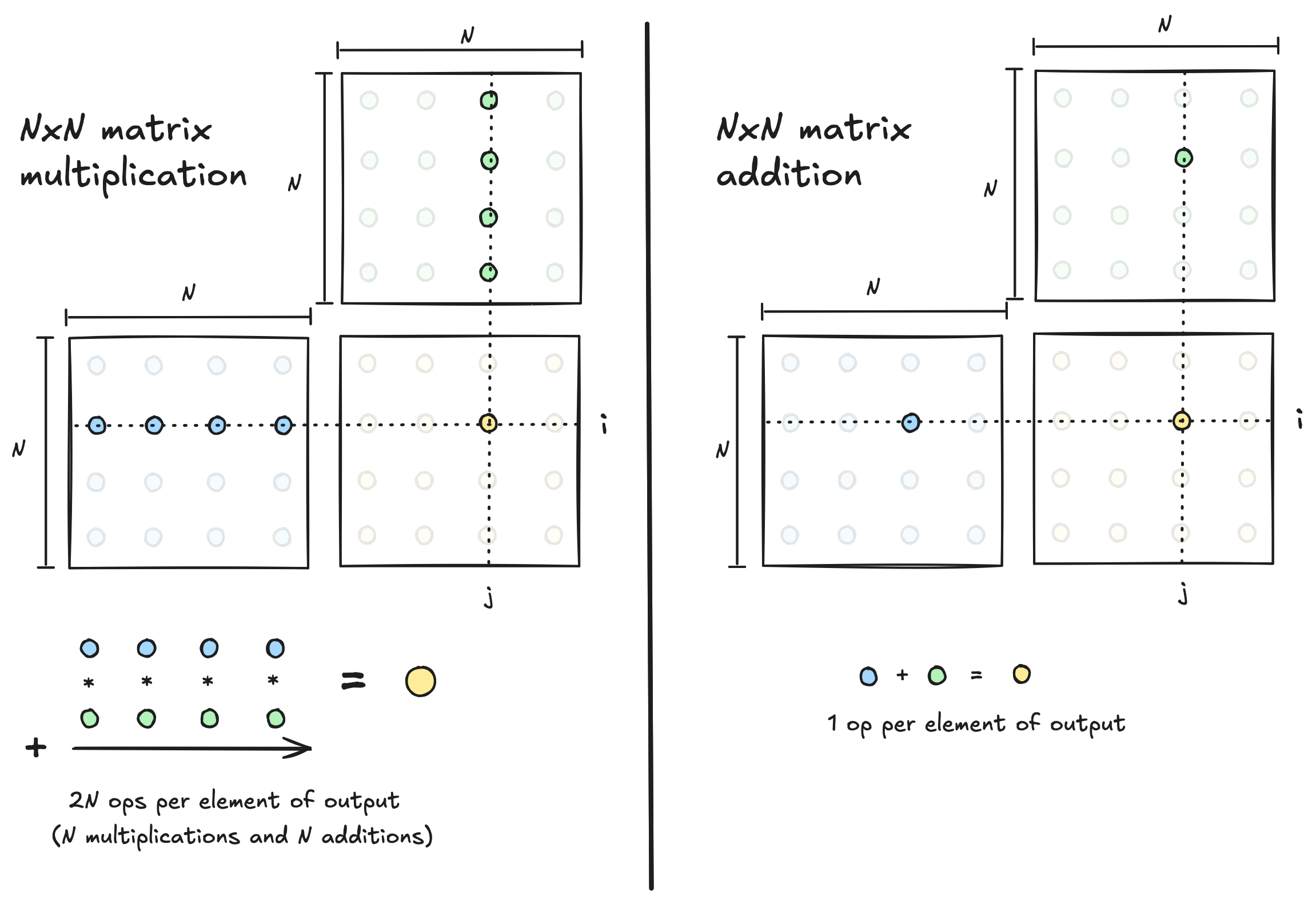
multiplication_vs_addition

在矩阵加法的情况下，计算单个输出元素需要一个算术操作，这意味着运行此算法时，数据移动和计算量总是直接成比例。如果我们相加两个 N×N 矩阵，涉及的数据量为 O(N²)，所需的计算量也是 O(N²)。因此，计算与数据的比率为 O(N²)/O(N²)=O(1)，这意味着矩阵加法在任何现代设备上可能都是内存受限的，无论我们编写多么巧妙的算法。相对于数据移动量，所需的数学运算并不多，因此可实现的算术强度上限较低。深度学习中的许多操作都属于这种低算术强度类别，一种称为内核融合的技术在此可能有所帮助。

然而，矩阵乘法并非注定是内存受限的，因为相对于问题规模，需要更多的算术运算。当相乘两个 N×N 矩阵时，涉及的数据量也是 O(N²)，但所需的计算量为 O(N³)（每个输出元素 O(N) 操作，乘以 O(N²) 个输出元素）。因此，计算与数据的比率为 O(N³)/O(N²)=O(N)。所需计算量比数据移动多一个因子 N。我们可以实现的算术强度上限随矩阵维度 N 增长。如果我们相乘足够大的矩阵，我们应该能够编写一个具有足够算术强度的算法，使其成为计算受限而非内存受限。

总之，我们实现的算术强度取决于我们编写的内核，并且必须小于或等于内核实现的算法所施加的上限。实现的算术强度，给定我们的机器参数 τ 和 β，决定了我们是内存受限还是计算受限。如果算法的算术强度上限允许，我们希望优化内核直到它成为计算受限而非内存受限。

简单计算机上可实现的算术强度¶

对于相乘两个 N×N 矩阵，我们可以实现的最佳算术强度是 O(N)。现在的问题是，当实际编写内核时，我们如何思考所有这些？要回答这个问题，我们需要一个运行计算机的模型，开始时我们将使用具有快速和慢速内存的简单计算机。

最坏情况¶

在简单计算机上，两个 N×N 矩阵相乘（C=A∗B）的第一个实现如下所示。我们在需要时立即加载每个值，并在完成后立即存储每个输出。计算与数据移动的比率是多少？它是否接近理想的 O(N)？

allocate registers a,b,c in fast memory
for i=1...N:
    for j=1...N:
        c = 0
        for k=1...N:
            load A(i,k) into a
            load B(k,j) into b
            c += a * b
        store c into C(i,j)

allocate registers a,b,c in fast memory
for i=1...N:
    for j=1...N:
        c = 0
        for k=1...N:
            load A(i,k) into a
            load B(k,j) into b
            c += a * b
        store c into C(i,j)

我对这个实现的心理模型大致如下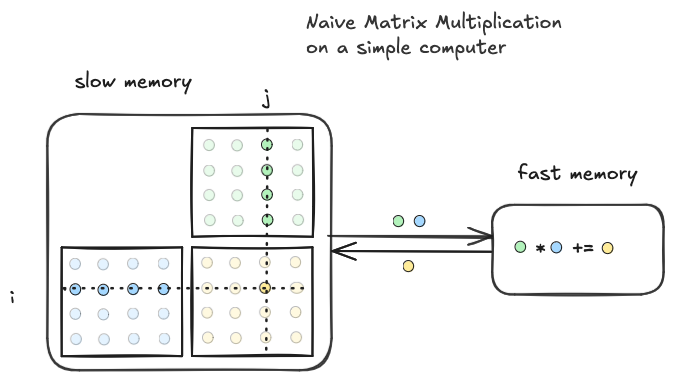 simple_computer_matmul_naive

这个实现在简单计算机上的算术强度是 O(1)，因为在内部循环的每次迭代中执行单个乘加操作，并且只加载该迭代期间操作的数据。有 O(N³) 的数据移动和 O(N³) 的计算，这意味着 O(N³)/O(N³)=O(1) 的强度，比理想情况差一个因子 O(N)。这被证明是最坏情况。

最佳情况¶

上述实现的不良强度是由于我们一次只从快速内存加载单个元素，仅在需要时加载。只有三个矩阵元素同时存储在快速内存中。我们可以通过更好地利用快速内存来提高强度。为了说明最佳情况，假设快速内存足够大，可以容纳整个 A、B 和 C。如果是这种情况，我们可以在快速内存中为 C 分配空间，预先传输整个 A 和 B，执行三个嵌套循环，所有数据已存在于快速内存中，然后完成后一次性将整个 C 矩阵存储回慢速内存。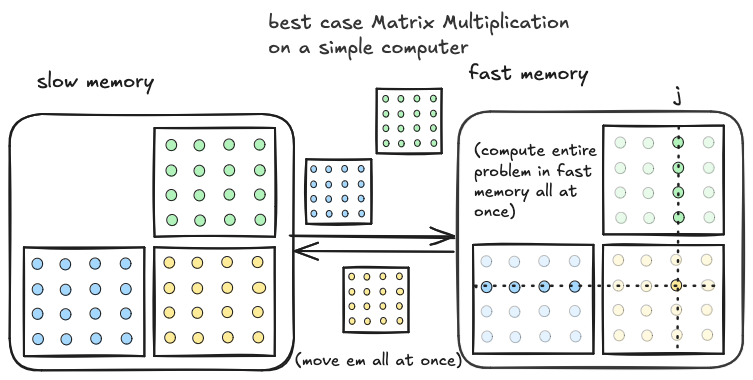 simple_computer_matmul_best_case 在这种情况下，由于我们只移动每个矩阵一次，数据移动为 O(N²)。计算与上述相同，为 O(N³)。查看两者的比率，我们实现了最佳情况强度，O(N³)/O(N²)=O(N)。然而，这是不现实的，因为整个问题通常无法放入快速内存。

现实情况¶

我们希望在慢速内存和快速内存之间一次移动多于三个元素。但我们不能一次性移动整个矩阵。我们可以通过移动 A 和 B 的子块（尽可能大以适合）来妥协。我们移动到快速内存的每对输入块对应一个输出块，可以通过快速内存中驻留的输入块之间的迷你矩阵乘法来计算。然后我们移动下一对输入块到快速内存并再次计算。

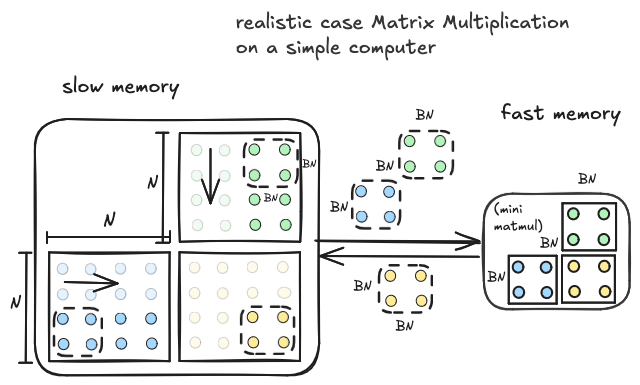
simple_computer_matmul_realistic_case

以下是与上图对应的伪代码：

Allocate A_tile[BN, BN], B_tile[BN,BN], C_tile[BN,BN] in fast memory

# outer loop over tiles of A and B
for i=1...N in steps of size BN:
    for j=1...N in steps of size BN:
        C_tile[: , :] = 0
        for k=1...N in steps of size BN:
            Load A[i : i+BN, k : k+BN] into A_tile
            Load B[k : k+BN, j : j+BN] into B_tile

            # inner loop, do a mini matmul between tiles of A and B
            # store the result in C_tile
            for tile_i=1...BN:
                for tile_j=1...BN:
                    for tile_k=1...BN:
                        C_tile[tile_i, tile_j] +=
                            A_tile[tile_i, tile_k] * B_tile[tile_k, tile_j]

        # once we have looped over all the tiles along the K dimension of A,B
        # store C_tile back to its place in slow memory
        Store C_tile into C[i : i + BN, j : j+BN]

Allocate A_tile[BN, BN], B_tile[BN,BN], C_tile[BN,BN] in fast memory

# outer loop over tiles of A and B
for i=1...N in steps of size BN:
    for j=1...N in steps of size BN:
        C_tile[: , :] = 0
        for k=1...N in steps of size BN:
            Load A[i : i+BN, k : k+BN] into A_tile
            Load B[k : k+BN, j : j+BN] into B_tile

            # inner loop, do a mini matmul between tiles of A and B
            # store the result in C_tile
            for tile_i=1...BN:
                for tile_j=1...BN:
                    for tile_k=1...BN:
                        C_tile[tile_i, tile_j] +=
                            A_tile[tile_i, tile_k] * B_tile[tile_k, tile_j]

        # once we have looped over all the tiles along the K dimension of A,B
        # store C_tile back to its place in slow memory
        Store C_tile into C[i : i + BN, j : j+BN]

计算与数据移动的比率是多少？它与最坏情况和最佳情况相比如何？我们可以通过查看循环结构来回答这些问题。

首先考虑数据移动。外部有三个嵌套循环，每个循环以 BN 大小的步长从 1 到 N 进行。每个循环迭代 N/BN 次，由于有三层嵌套，嵌套循环体内的内容将发生(N/BN)^3 次。在循环嵌套内部，我们加载两个大小为 BN^2 的图块，分别对应两个输入矩阵。渐近地，这导致 O((N/BN)^3 * BN^2)的数据移动（我们可以忽略存储操作，因为它只发生在两个循环嵌套内部，仅发生(N/BN)^2 次）。约简后得到 O(N^3/BN)的数据移动。注意，这比朴素情况少了一个 BN 因子的数据移动。C_tile，因为它只发生在两个循环嵌套内部，仅发生(N/BN)^2 次）。约简后得到 O(N^3/BN)的数据移动。注意，这比朴素情况少了一个 BN 因子的数据移动。

现在计算。与上述相同，我们有三个嵌套循环，这个循环体的内部将执行(N/BN)^3 次。在循环嵌套内部，计算包括两个 BN 乘 BN 图块之间的迷你矩阵乘法，三个嵌套循环总共有 O(BN^3)步，这是我们期望的将两个 BN 乘 BN 矩阵相乘的步骤。因此总计算量为 O((N/BN)^3 * BN^3)，简化为 O(N^3)。这是两个 N 乘 N 矩阵相乘的期望步骤数，与朴素情况相同。

因此，这种分块方法具有与朴素实现相同的计算步骤数，但数据移动少了一个 O(BN)因子。算术强度计算为 O(N^3 / (N^3/BN)) = O(BN)。用英语来说，这告诉我们实现的算术强度将与我们适应快速内存的图块维度成线性比例。

总结¶

最终的结论相当直观。当乘以两个 N 乘 N 矩阵时，我们能实现的最佳强度与矩阵维度 N 成比例。然而，达到这个上限需要将整个 O(N^2)大小的问题放入快速内存，这通常不可能。因此，我们通过将 O(N^2)大小的问题分解为许多较小的 O(BN^2)大小的问题来妥协，并选择 BN 使得所有快速内存都被填满。然后我们能实现的强度与 BN 成比例。因此，在实践中，我们能实现的强度受限于设备上快速内存的大小。

GPU 上的并行矩阵乘法¶

思考简单计算机上的矩阵乘法有助于建立直觉，了解如何利用内存层次结构来获得更高的算术强度，这将有助于最大化我们内核的性能。然而，简单计算机模型有点过于简化，它包含一个两级内存层次结构和一些可以以速率τ对快速内存中的数据执行的计算。我们的目标是编写一个在 GPU 上运行的快速矩阵乘法内核，这引出了 GPU 与简单计算机有何不同的问题。

在最基本的层面上，答案是 GPU 与简单计算机一样，具有内存层次结构。但在 GPU 上，内存层次结构嵌套在并发计算单元的层次结构中。这是一个简单 GPU 的图示，说明了这一点。

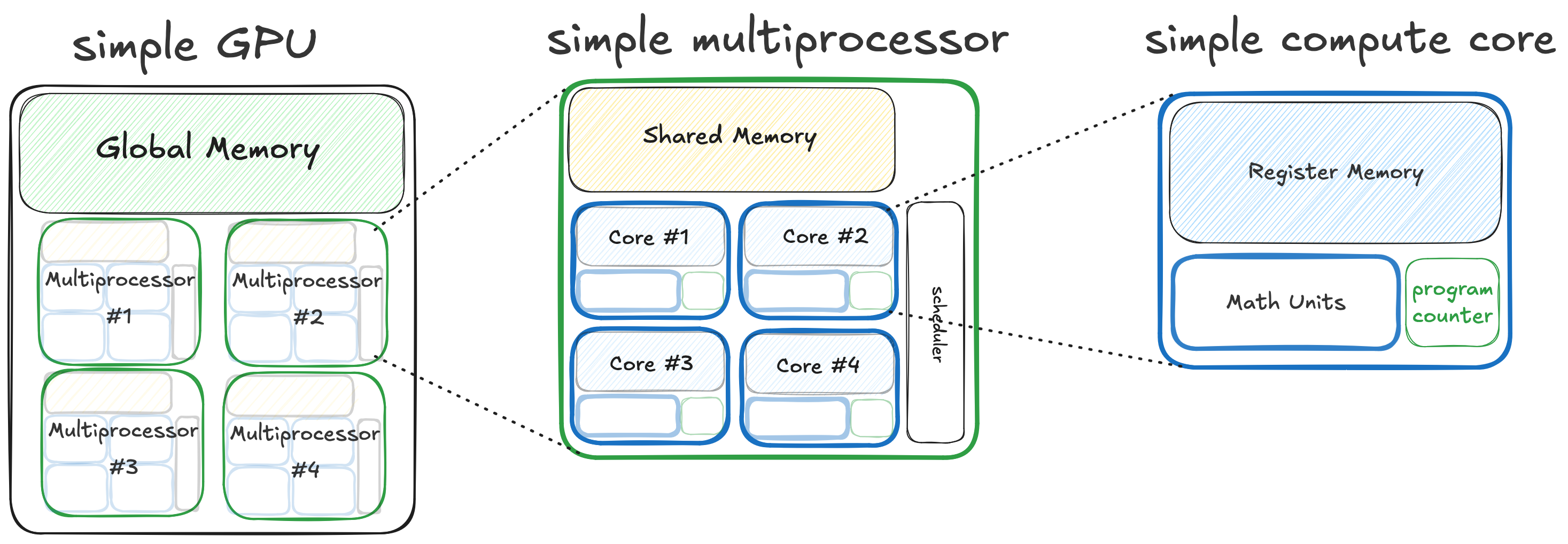
simple_gpu

在简单 GPU 上，组合的计算/内存层次结构有三个级别。

最高级别是整个 GPU，它拥有一大块 DRAM（全局内存）。GPU 由四个多处理器组成，每个都是独立的计算单元，彼此并发运行，并且都可以读写相同的 DRAM。
中间级别是多处理器，它拥有一块 SRAM（共享内存），并由四个核心组成，这些核心是独立的计算单元，可以并发运行，并且都可以读写多处理器本地的相同共享内存。
最低级别是单个计算核心，它拥有一些私有寄存器内存，并且可以独立于计算机的其他部分执行单个线程并进行算术运算。

分层分块（简单 GPU）¶

那么，我们如何使用这种类型的计算机来执行矩阵乘法？第一个有用的观察是，矩阵乘法问题可以分层分解为嵌套的图块。这是个好消息，因为分层算法非常适合分层计算机。

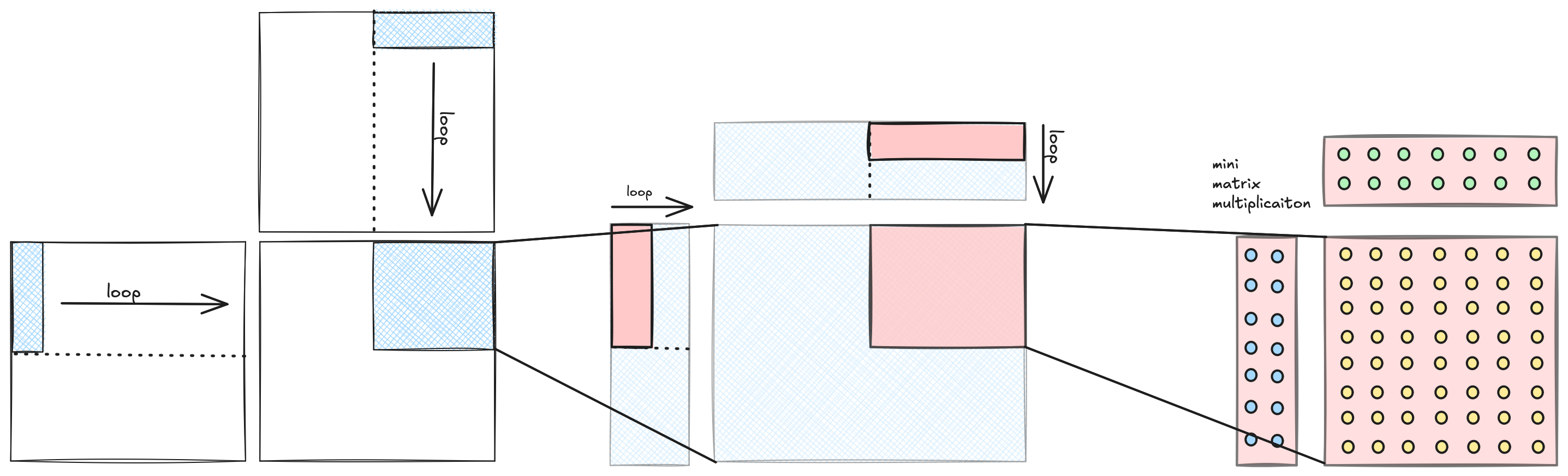
matmul_hierarchies

如果我们计算矩阵乘法 C=A*B，我们可以将输出矩阵 C 划分为不重叠的图块，并将每个图块分配给一个计算单元。这些输出图块中的每一个都可以通过输入对应图块之间的矩阵乘法来计算，独立于其他图块。由于我们的机器是分层的，计算单元内部还有计算单元，相应地，矩阵乘法内部还有矩阵乘法。我们递归地将问题分解为嵌套图块，直到达到计算的原子元素，物理上通常是某种类型的单个核心，逻辑上是单个执行线程。在这个级别，单个线程计算其输入图块之间的小矩阵乘法。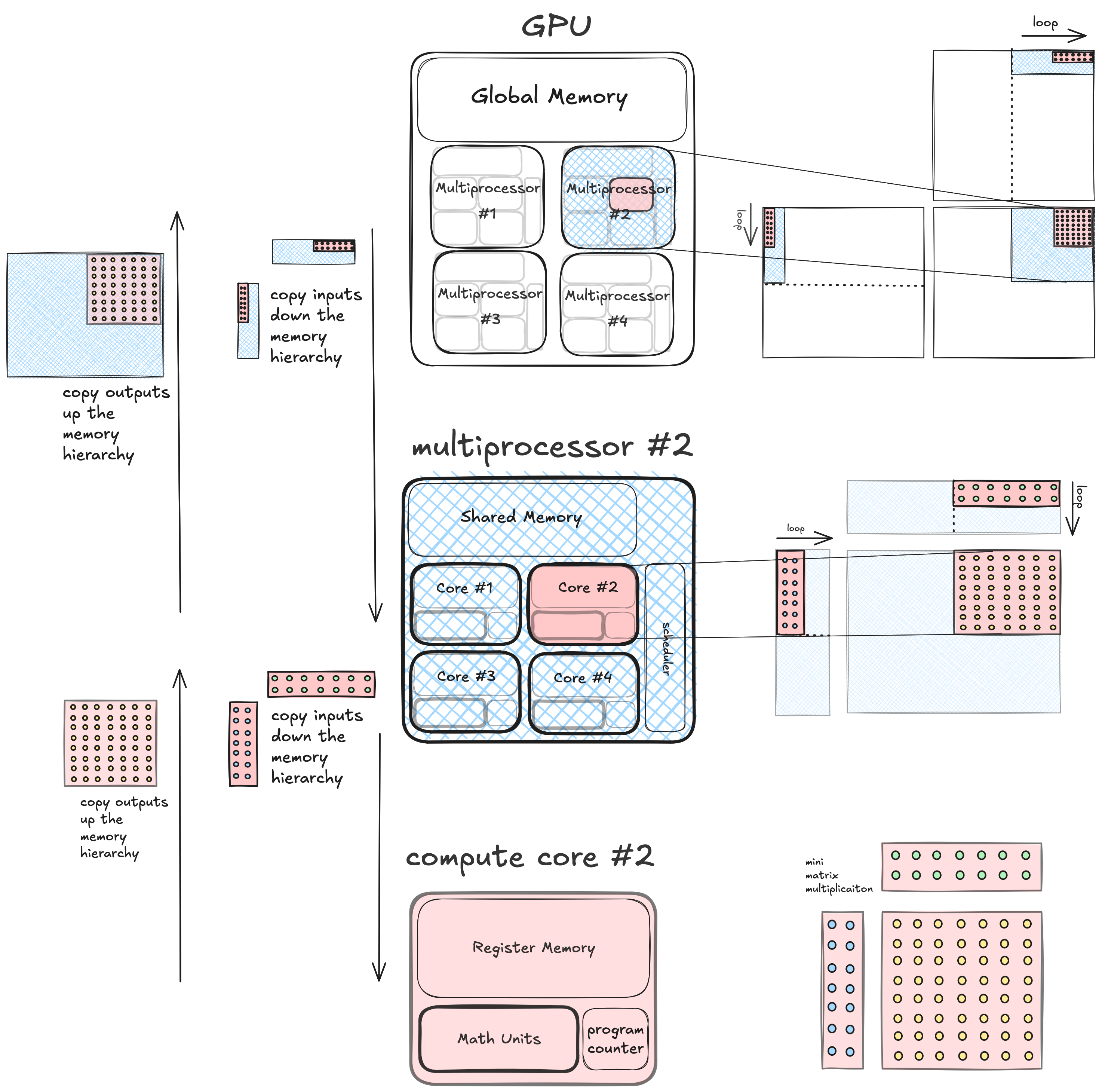 hierarchy_combined

分层分块（真实 GPU）¶

上图显示了 GPU 实现分层分块的粗略、高级视图。在 NVIDIA GPU 上使用 CUDA 实现时，我们需要填充一些更精细的细节。这种分块结构通过以下方式创建：

一系列固定维度的全局、共享和寄存器内存分配
控制图块位置的嵌套循环
多处理器内运行线程之间的同步点
最低级别的计算，在这种情况下是在张量核心上运行的小矩阵乘法

这个内核是我的起点，但如果你有兴趣阅读一系列构建到类似内核的 10 个内核，我推荐阅读这个。

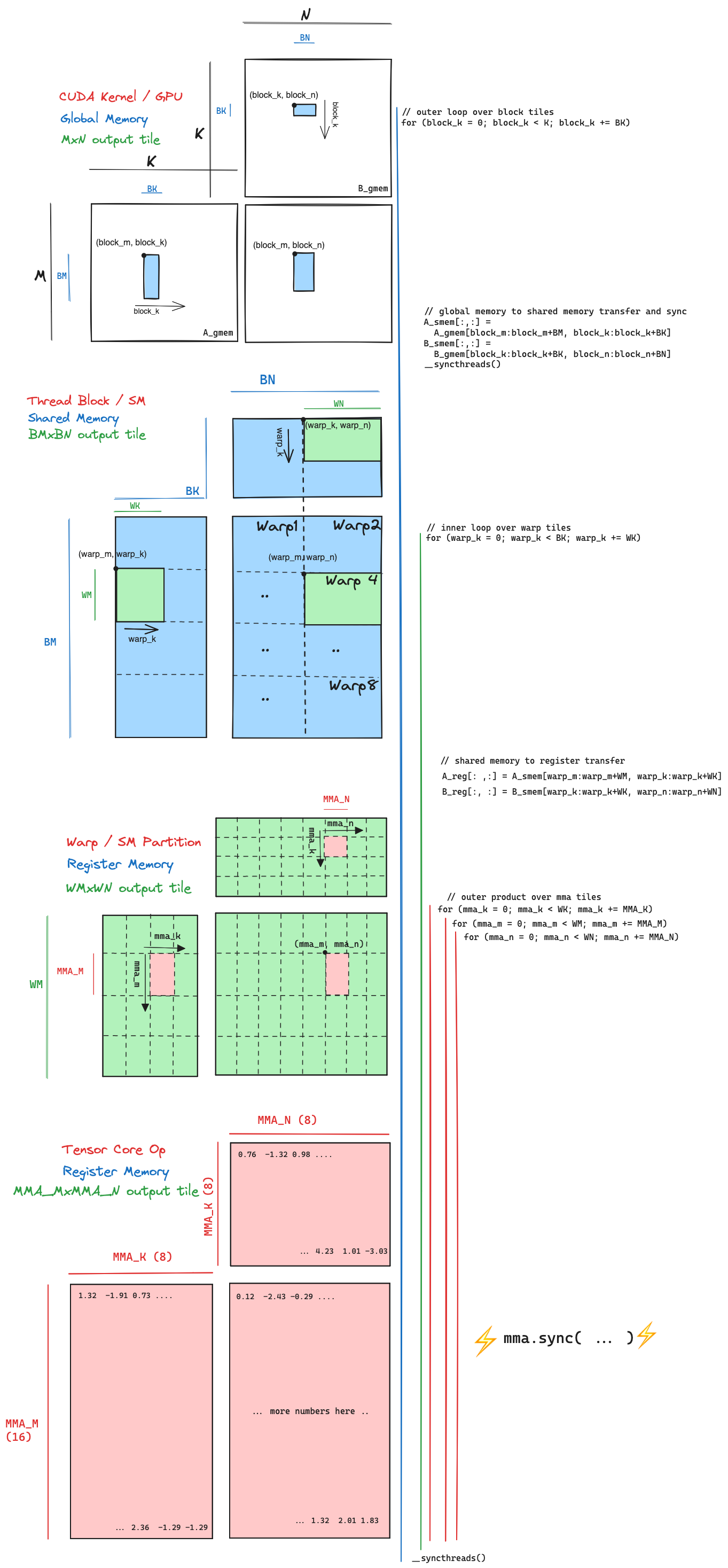
tiling

通过此图表，我试图展示循环嵌套与分块结构之间的对应关系。共有四个层级，每个层级对应计算层次、内存层次和分块形状的一个级别。

以下是从相关计算单元角度对每个层级的简要描述：

CUDA 内核 / GPU 层级：GPU 从 全局内存 读取三个输入矩阵 A、B 和 C，并将输出矩阵 D 写入全局内存。每个线程块在 A 和 B 的 K 维度（即“内部”维度）上循环。此循环以步长 block_k 递增 BK。在每次迭代中，我们将蓝色块分片从全局内存复制到共享内存。
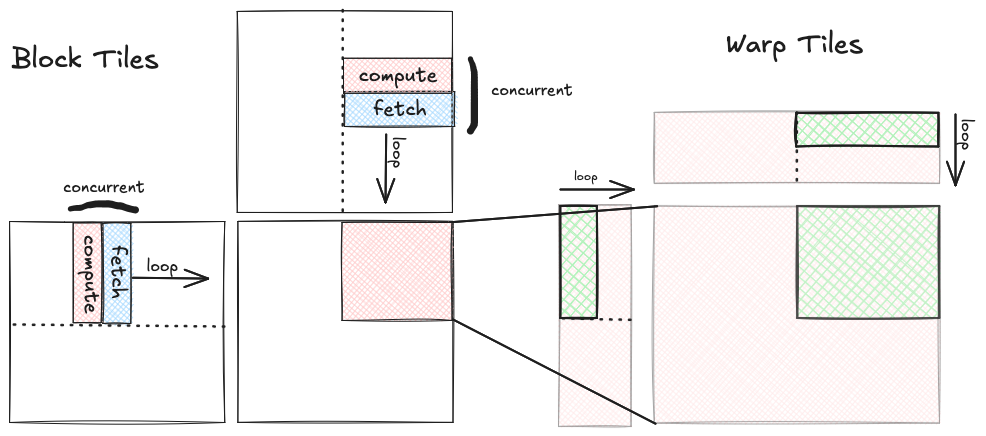
线程块 / SM 层级：此时，特定线程块计算输出 BM,BN 分片所需的 A 和 B 的蓝色子分片已被复制到 共享内存。此线程块在 GPU 的 16 个 SM 之一上运行，共享内存是该 SM 本地的，访问速度快。线程块内有 256 个线程，即 8 个线程束，每个包含 32 个线程。在线程块内，输出的 BM,BN 分片被划分为 8 份，以便 8 个线程束可以并发计算。每个线程束在块分片内的内部维度上循环，此循环以步长 warp_k 递增 WK。在每次迭代中，我们将绿色线程束分片从共享内存复制到寄存器内存。
线程束 / SM 分区：此时，蓝色块分片内的绿色线程束分片已被复制到 寄存器内存，特定线程束负责计算输出的 Turing SM 上 4 个分区之一运行WM 乘以 WN 分片。每个线程束通过取 A 的 WM,WK 分片与 B 的 WK,WN 分片的外积来计算其输出分片。在计算外积的三个嵌套循环内部，我们执行 MMA 同步操作。
张量核心操作：最后我们到达层次结构的最底层，即单个张量核心操作，这是一个硬件加速的 (16,8) x (8,8) = (16,8) 矩阵乘法，在 寄存器内存 中进行。

真实 GPU 上的性能考量¶

在针对特定 GPU 架构实现此结构的 CUDA 内核时，由于我们试图从硬件中榨取最后一滴性能，必须考虑许多因素。我将性能考量分为三类，本文其余部分讨论的每个优化都落入其中一类或两类。

算术强度作为分块维度的函数¶

实现高算术强度的必要性是我们拥有这种分块嵌套结构的原因，而分块维度是我们可调节的主要旋钮，决定了内核的算术强度。在我们的内核中，我们首先将数据从全局内存加载到共享内存，然后从共享内存加载到寄存器。在这两种情况下，我们都在将对应于输入数据的两个矩形分片从较慢的内存加载到较快的内存，并最终在层次结构的最底层计算这两个输入之间的矩阵乘法。我们应实现的算术强度是我们选择的分块维度的函数（越大越好），如下所示。

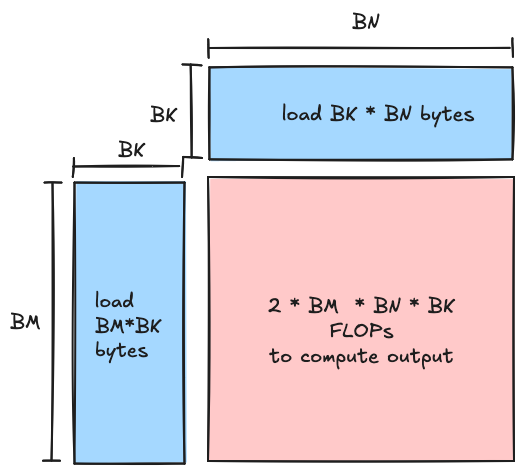
intensity_tile_dims

FLOPs：在内部循环的每次迭代中，每个线程块将形状为 (BM,BK) 的矩阵与形状为 (BK,BN) 的矩阵相乘，以产生输出的 (BM,BN) 分片。此矩阵乘积包含 2∗BM∗BK∗BN FLOPs（在维度上的三个嵌套循环，内循环中有乘加操作）
内存：形状为 (BM,BK) 和 (BK,BN) 的矩阵在每次迭代中从全局内存读取，由于每个元素为两个字节，总共读取 2(BM∗BK+BK∗BN)=2BK(BM+BN) 字节，我们在内部循环中不执行任何写入，所有写入都在内核尾声进行。

取这两者的比值，对于给定块分片大小，我们应实现的算术强度恰好为 BM∗BN/(BM+BN) FLOP/字节。对于层次结构第二级的线程块级分片，我们将希望选择分块维度，使此比值大于张量核心相对于全局内存的平衡点，但会受到共享内存大小的限制。同样，对于层次结构下一级的线程束分片，我们将希望选择分块维度，使此比值大于张量核心相对于共享内存的平衡点，但会受到寄存器内存大小的限制。前者比后者更具挑战性。

计算与数据移动之间的重叠¶

屋顶线模型给出了算术吞吐量的上限 Tmax=min(β∗I,τ)。为了实现此上限，我们需要计算与数据移动之间的完美重叠。为了理解原因，假设我们实现了足够的算术强度，使我们处于屋顶线模型的计算受限区域。此时，为了使我们的实际吞吐量等于上限 Tmax=τ，我们需要持续计算，任何计算空闲时间都意味着实际吞吐量低于机器峰值 τ。有许多原因会导致计算空闲，例如内存延迟、数据依赖性和同步点。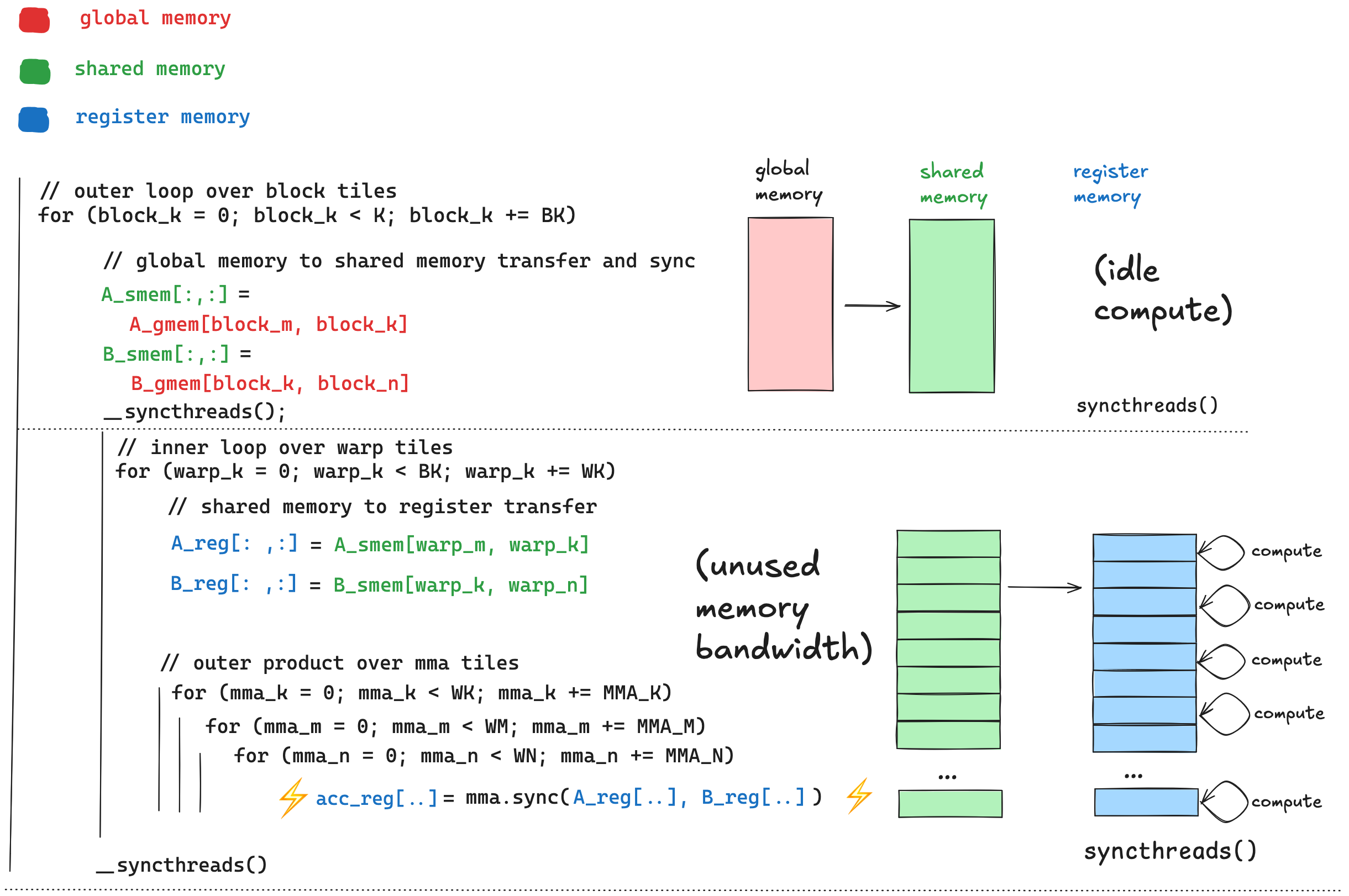 compute_data_movement_overlap 如上所示，我们初始的循环结构在这方面存在一些低效之处。

最大化内存带宽¶

根据非官方基准测试T4 上可达到的最佳全局内存带宽约为 220 GB/秒，最佳共享内存带宽约为 3662 GB/秒。然而，未经优化的内核只能达到这些数值的一小部分。首要考虑因素是访问模式；当相邻线程组请求内存时，某些线程到内存中数据的映射比其他映射更高效。实现全局内存与共享内存的硬件功能不同，因此，对于读取共享内存最优的访问模式可能对读取全局内存并非最优。

全局内存访问的主要考虑因素称为合并（coalescing），一句话总结是：当相邻线程访问全局内存中的相邻数据时，可实现最大全局内存带宽（解释此处）。共享内存将在[后续](#背景 bank 冲突和 wavefronts)章节中深入探讨。

如何使用张量核心¶

本节简要概述使用张量核心的机制。

所有 tensor core 操作都在计算层次结构的 warp 级别执行；32 个线程协作将数据加载到其寄存器中，然后同步执行小型硬件加速矩阵乘法。在设计 tensor core 算法时，我们应将 warp 视为计算的基本单元，尽管实际上一个 warp 包含 32 个能够独立操作的线程。相比之下，如果我们编写不使用 tensor core 的 GEMM 内核，执行标量乘加操作的单个线程将是我们的计算基本单元。

Tensor core 可通过两种不同方法访问。第一种是通过wmma api，它是 CUDA 工具包的一部分。wmma似乎被认为是更可移植但性能较低的方式来编程 tensor core。我很快放弃了它，因为它抽象了将输入数据从共享内存加载到寄存器内存的过程，而事实证明这里的一些细节对性能至关重要。

另一种途径是使用mma指令家族，它们是 PTX 的一部分，此选项比wmma途径更灵活且性能更高。PTX 是 NVIDIA GPU 的中间表示，比 CUDA 低级，但比 SASS（这是 NVIDIA GPU 运行的汇编语言）高级。PTX 可以内联在内核中以调用 tensor core。

我使用的 PTX 指令是mma.sync.aligned.m16n8k8.row.col.f16.f16.f16.f16（文档此处），该指令的每个部分都有含义：

mma：我们正在执行矩阵乘加操作
sync：此指令是同步的，所有 32 个线程将等待所有 32 个线程完成后再恢复执行
aligned：warp 中的所有 32 个线程必须执行此指令，如果 warp 中少于 32 个线程执行此指令，行为未定义
m16n8k8：这是矩阵片段形状的标识符。这意味着矩阵 A 的片段形状为 (16,8)，B 的片段形状为 (8,8)，D 和 C 的片段形状为 (8,8)。（记住，GEMM 的公式是 D=α∗A∗B+β∗C）。如果您查看上面链接的 PTX 文档，有许多不同的形状可供选择，但 Turing/Volta 架构仅支持有限数量。Ampere 支持更多，Hopper 支持更多。
row：A 片段应以行主序布局存储在寄存器中
col：B 片段应以列主序布局存储在寄存器中
f16：D 是 fp16 矩阵
f16：A 是 fp16 矩阵
f16：B 是 fp16 矩阵
f16：C 是 fp16 矩阵

每个mma.sync指令期望 warp 中 32 个线程的寄存器中片段元素的特定布局，这些布局可在 PTX 文档中找到。这是m16n8k8布局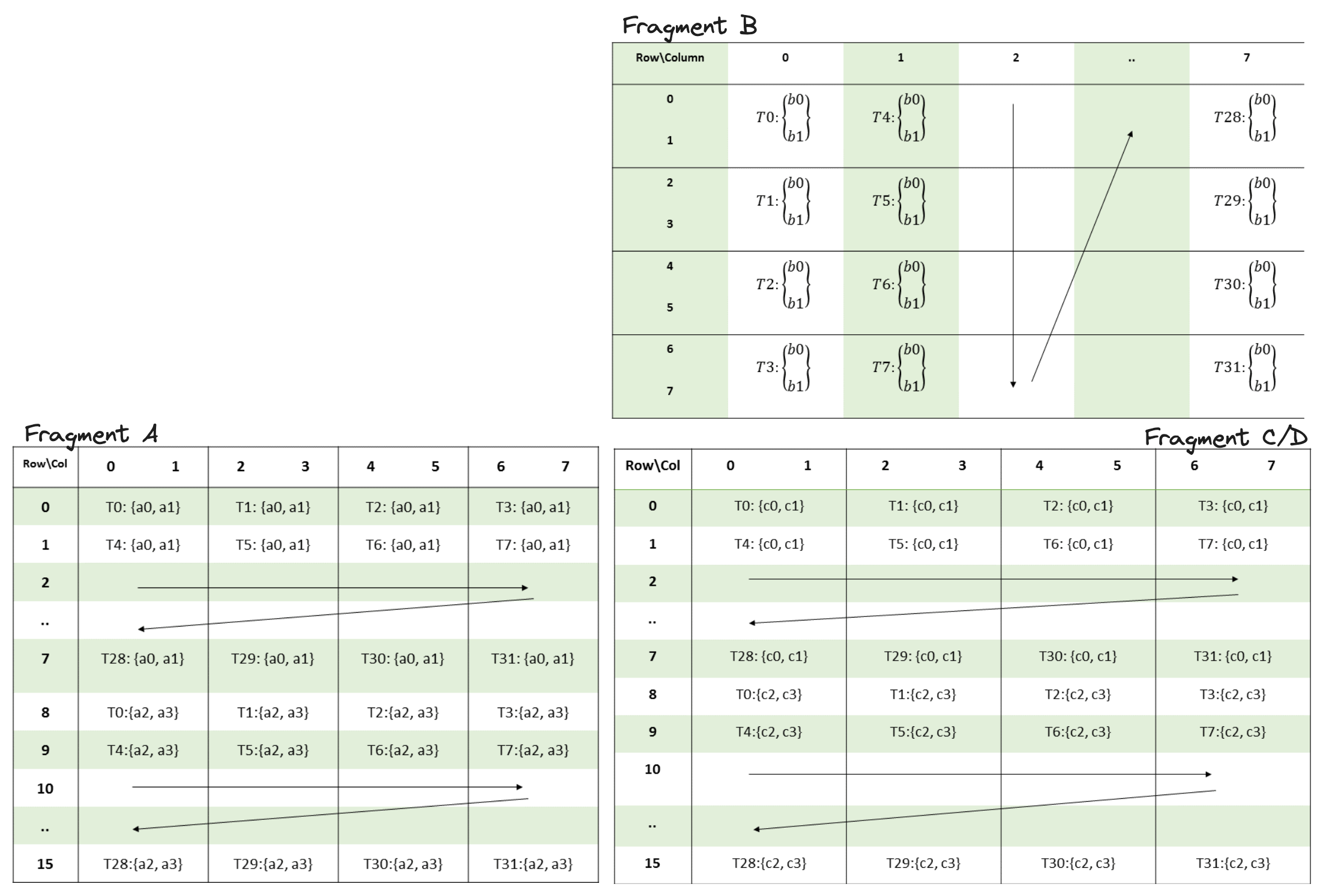： matrix_fragments

这些图描述了线程、寄存器和矩阵元素之间的映射：

T0, T1, T2 ...指线程的索引。这些图中的线程索引范围为 0-31，因为一个 warp 有 32 个线程。
a0, a1, a2, ... b0, b1, b2, ... c0, c1, c2指保存矩阵元素的寄存器。
每个线程/寄存器对的位置告诉我们哪些矩阵元素进入哪个线程的哪个寄存器。例如，T0: {a0,a1}位于矩阵片段 A 的左上角，这意味着此片段中的元素(0,0)和(0,1)被放置在寄存器a0和a1的线程 0 中。

幸运的是，还有另一个 PTX 指令称为ldmatrix（文档此处），它从共享内存加载矩形数据块，并在 warp 内洗牌矩阵元素以创建此布局。它可以在将矩阵元素从共享内存移动到寄存器时选择性地转置矩阵元素，这对于上面的矩阵 B 很方便，矩阵 B 是列主序或“转置”布局。

我们内核的内循环将包括重复调用ldmatrix以将数据从共享内存移动到寄存器内存，然后重复调用m16n8k8变体以使用 tensor core 将块相乘。对于此项目，我使用了 Turing 架构 GPU，在 Ampere 上 tensor core API 非常相似，但支持更多矩阵形状。在 Hopper 上，API 大幅扩展，引入了 PTX 指令，允许 128 个线程组异步执行比mma.sync大得多的矩阵乘法。m16n8k8。

内核¶

在本文的其余部分，我将讨论一系列内核，这些内核使我在 8192x8192 矩阵的 tensor core GEMM 上达到了约 96% 的 cuBLAS 性能水平。每个内核都建立在前一个的基础上，每个的主题是：

分层分块
向量化/展开的 gmem->smem 传输
[共享内存重排](#swizzling 玩具示例)
[临时异步复制](#内核 4---临时异步复制)
调整块维度
优化索引计算
[双缓冲](#内核 6---双缓冲)

内核 1 - 分层分块¶

我编写的第一个内核实现了[上方](#分层分块真实 gpu)所示的分层分块结构。以下是执行矩阵乘法的循环结构的伪代码。

// outer loop over block tiles
for (block_k = 0; block_k < K; block_k += BK)
{
    // global memory to shared memory transfer
    A_smem[:,:] = A_gmem[block_m:block_m+BM, block_k:block_k+BK]
    B_smem[:,:] = B_gmem[block_k:block_k+BK, block_n:block_n+BN]

    // synchronize across the thread block in between
    // writing shared memory and reading shared memory
    __syncthreads();

    for (warp_k = 0; warp_k < BK; warp_k += WK)
    {
        // load from shared memory into register memory in preparation for compute phase
        A_reg[: ,:] = A_smem[warp_m:warp_m+WM, warp_k:warp_k+WK]
        B_reg[:, :] = B_smem[warp_k:warp_k+WK, warp_n:warp_n+WN]

        // outer product over mma tiles
        for (mma_k = 0; mma_k < WK; mma_k += MMA_K)
        {
            for (mma_m = 0; mma_m < WM; mma_m += MMA_M)
            {
                for (mma_n = 0; mma_n < WN; mma_n += MMA_N)
                {
                    mma_sync_m16n8k8(
                        acc_reg[mma_m:mma_m+MMA_M, mma_n:mma_n+MMA_N],
                        A_reg[mma_m:mma_m+MMA_M, mma_k:mma_k+MMA_K],
                        B_reg[mma_k:mma_k+MMA_K, mma_n:mma_n+MMA_N],
                        acc_reg[mma_m:mma_m+MMA_M, mma_n:mma_n+MMA_N]
                    )

                }
            }
        }
    }
    __syncthreads();

}

// outer loop over block tiles
for (block_k = 0; block_k < K; block_k += BK)
{
    // global memory to shared memory transfer
    A_smem[:,:] = A_gmem[block_m:block_m+BM, block_k:block_k+BK]
    B_smem[:,:] = B_gmem[block_k:block_k+BK, block_n:block_n+BN]

    // synchronize across the thread block in between
    // writing shared memory and reading shared memory
    __syncthreads();

    for (warp_k = 0; warp_k < BK; warp_k += WK)
    {
        // load from shared memory into register memory in preparation for compute phase
        A_reg[: ,:] = A_smem[warp_m:warp_m+WM, warp_k:warp_k+WK]
        B_reg[:, :] = B_smem[warp_k:warp_k+WK, warp_n:warp_n+WN]

        // outer product over mma tiles
        for (mma_k = 0; mma_k < WK; mma_k += MMA_K)
        {
            for (mma_m = 0; mma_m < WM; mma_m += MMA_M)
            {
                for (mma_n = 0; mma_n < WN; mma_n += MMA_N)
                {
                    mma_sync_m16n8k8(
                        acc_reg[mma_m:mma_m+MMA_M, mma_n:mma_n+MMA_N],
                        A_reg[mma_m:mma_m+MMA_M, mma_k:mma_k+MMA_K],
                        B_reg[mma_k:mma_k+MMA_K, mma_n:mma_n+MMA_N],
                        acc_reg[mma_m:mma_m+MMA_M, mma_n:mma_n+MMA_N]
                    )

                }
            }
        }
    }
    __syncthreads();

}

它实现的 8% cuBLAS 吞吐量是起点。本文的其余部分深入探讨了我用来使其更快的一些技术。

table1

内核 2 - 向量化内存复制和循环展开¶

为了提高我们代码的性能，我们需要知道它为什么慢。在编写 CUDA 内核时，用于此目的的最佳工具称为 NSight Compute，这是由 NVIDIA 开发的分析器，在内核执行时提供大量关于硬件中发生情况的详细指标。我通常首先查看名为“Warp State Statistics（Warp 状态统计）”的部分。当内核执行时，每个 warp（线程束）都由调度器发出指令。在理想情况下，调度器每个时钟周期都能发出新指令。在现实世界中，很难编写出每个周期都能发出新指令的内核，有各种原因导致在给定周期内，warp 可能无法执行其下一条指令，而是会“停滞（stall）”，即什么都不做。停滞的原因可能包括各种硬件管道的容量限制、内存延迟或内核中的同步点，这些同步点要求运行在 SM 上的所有线程等待所有其他线程赶上。Warp 状态统计部分告诉我们，平均每个 warp 在每个发出的指令上花费多少时钟周期停滞，按多个不同类别细分。这为我们提供了所需信息，以将优化目标对准内核中性能最差的部分。以下是 Kernel 1 的 Warp 状态部分的截图。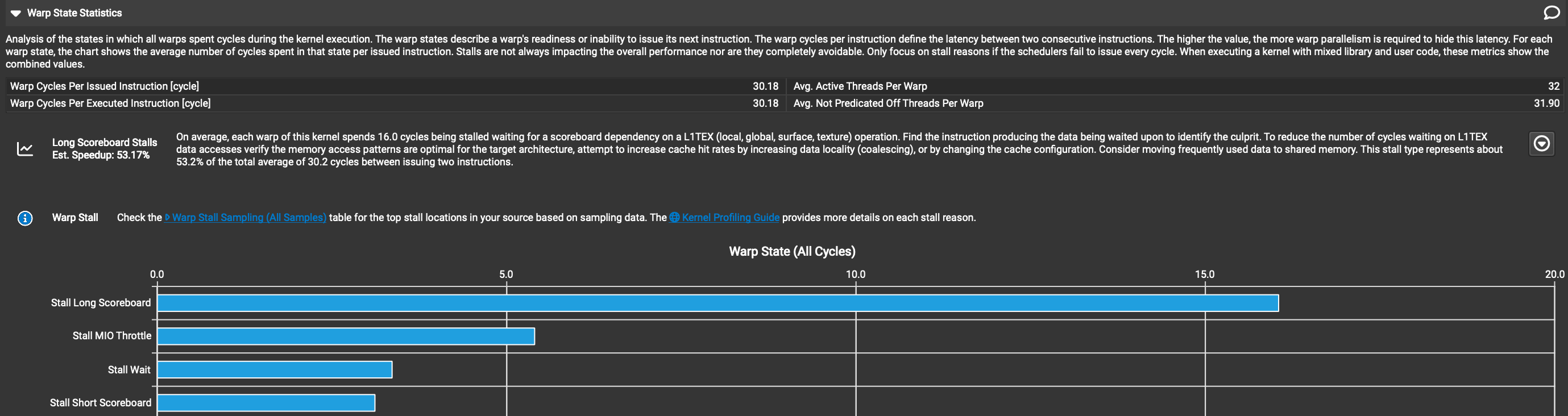 warp_state_kernel1 “Warp Cycles Per Issued Instruction（每个发出指令的 Warp 周期）”字段告诉我们，平均每个发出的指令，warp 大约花费约 30 个周期空闲，下表告诉我们这 30 个周期中有 16 个是由于“Long Scoreboard（长记分牌）”停滞类别。

Scoreboarding（记分牌）是大多数处理器硬件中实现的一种算法，用于跟踪下一条指令的数据依赖何时到达寄存器中，以便指令执行。大多数现代 CPU 能够动态重新排序指令，使得操作数已就绪的指令可以在操作数尚未到达寄存器的指令之前执行。重新排序在硬件中完成，受后续指令之间数据依赖的约束。这被称为out of order execution（乱序执行），它是一种相当高级的技术，用于隐藏延迟。GPU 在执行时不重新排序指令，我猜想是因为所需逻辑消耗了芯片上相当数量的宝贵晶体管，而且由于 GPU 是为throughput（吞吐量）设计的，这些晶体管最好用于张量核心等事物。

然而，GPU 确实跟踪数据依赖，但与 CPU 相比，编译器提供了更多帮助。当执行下一条指令所需的数据尚未到达寄存器内存时，正在执行的 warp 只是等待其数据到达。“Long Scoreboard Stall（长记分牌停滞）”近似表示 warp 因等待数据依赖而停滞的平均周期数。这一停滞原因占 warp 空闲所有周期约 50%的事实告诉我们，Kernel 1 的性能主要受内存延迟限制。这告诉我们应专注于将数据从全局内存移动到芯片上的代码，并找出如何最小化每字节移动的延迟。

从全局内存读取矩形数据块，并将其写入共享内存，是内核外循环每次迭代中发生的第一件事。最简单的方法是让相邻线程访问全局内存中的相邻值，并以与全局内存中相同的布局将数据写入共享内存。这种访问模式对于读取全局内存和写入共享内存都是最优的。以下是我编写的第一个数据传输：

__device__ void tileMemcpy(
    half* src,
    half* dst,
    const unsigned int src_stride,
    const unsigned int tile_rows,
    const unsigned int tile_cols
)
{
    // flatten out 2d grid of threads into in order of increasing threadIdx.x
    const unsigned int thread_idx = threadIdx.y * blockDim.x + threadIdx.x;
    const unsigned int num_threads = blockDim.x * blockDim.y;
 
    // # of threads is multiple of # of columns in the tile
    assert(num_threads % tile_cols == 0);
 
    // assign each thread a row/column in the tile, calculate the row step
    const unsigned int row_step = num_threads / tile_cols;
    const unsigned int thread_row = thread_idx / tile_cols;
    const unsigned int thread_col = thread_idx % tile_cols;
 
    for (unsigned int r = thread_row; r < tile_rows; r+=row_step)
    {
        dst[r * tile_cols + thread_col] =  src[r * src_stride + thread_col];
    }
}

__device__ void tileMemcpy(
    half* src,
    half* dst,
    const unsigned int src_stride,
    const unsigned int tile_rows,
    const unsigned int tile_cols
)
{
    // flatten out 2d grid of threads into in order of increasing threadIdx.x
    const unsigned int thread_idx = threadIdx.y * blockDim.x + threadIdx.x;
    const unsigned int num_threads = blockDim.x * blockDim.y;
 
    // # of threads is multiple of # of columns in the tile
    assert(num_threads % tile_cols == 0);
 
    // assign each thread a row/column in the tile, calculate the row step
    const unsigned int row_step = num_threads / tile_cols;
    const unsigned int thread_row = thread_idx / tile_cols;
    const unsigned int thread_col = thread_idx % tile_cols;
 
    for (unsigned int r = thread_row; r < tile_rows; r+=row_step)
    {
        dst[r * tile_cols + thread_col] =  src[r * src_stride + thread_col];
    }
}

查看与此tileMemcpy函数在godbolt中对应的 SASS，我们可以看到循环内的复制操作dst[...] = src[...]从 SASS 的低级视角编译为两个操作：从全局内存的两字节加载（SASS 中的LDG.U16），接着是两字节存储（STS.U16），以及一堆索引计算和循环开销。长记分牌停滞阻止存储发生，直到我们加载的值已到达寄存器。

以下是此循环如何执行的视觉化，针对单个线程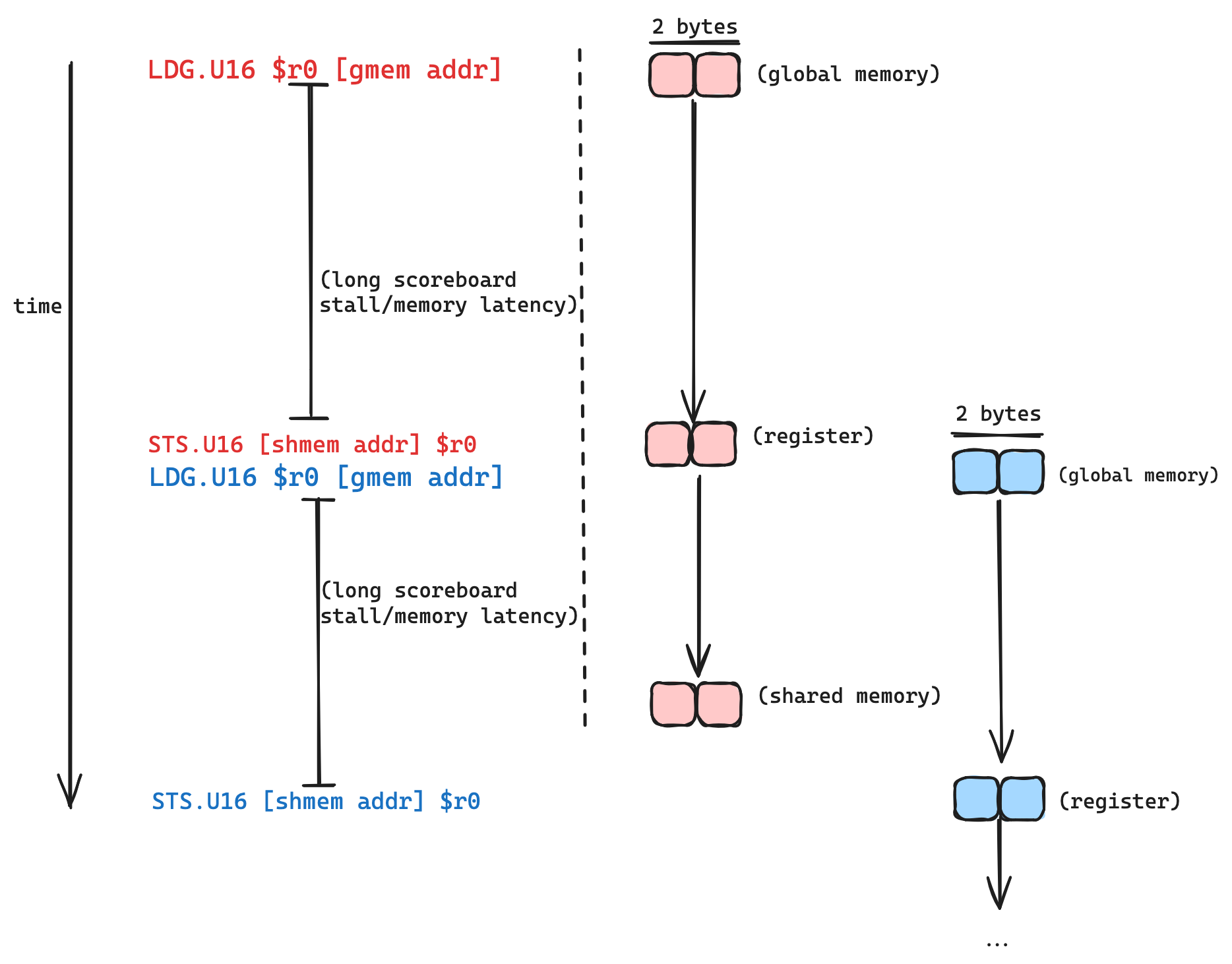： memory_latency 加载和存储之间的延迟是不可避免的：请求发送到 DRAM 控制器，数据从 DRAM 获取，然后通过总线传输。除非我们破解物理定律或发明时间机器，否则无法消除延迟。但我们可以做的是隐藏它。

延迟隐藏是计算中的一个核心概念，其核心非常简单。它只是意味着，如果我们执行具有某些延迟的操作 X，我们希望在 X 发生时做其他有用工作，而不是等待并无所事事。例如，如果我醒来决定想要一个煎蛋卷，我会先打开炉子让锅预热，同时我会打鸡蛋和磨碎奶酪。这种操作顺序通过打鸡蛋和磨碎奶酪隐藏了预热锅的延迟。如果我饿了并渴望尽快吃到完成的煎蛋卷，站在那里无所事事地看着锅预热将是愚蠢的。

同样的原则适用于隐藏tileMemcpy中全局内存加载的延迟。由于复制操作发生在循环内，每个线程执行多次加载和多次存储，顺序如load (stall) store, load (stall) store, ...。如果我们能够重新排列这些，使顺序变为load load load (stall) store, store, store。在后一种排序中，三个加载请求的数据将同时传输，我们可以说每个加载的延迟被其他加载隐藏。实现后一种排序的最简单方法是通过在tileMemcpy中展开循环。如果我们能展开循环，nvcc应该足够智能地重新排序指令，以便全局内存加载能够相互隐藏延迟。在这种情况下，编译器为我们做了 CPU 在硬件上动态执行的工作。

如果我们想要展开循环，循环迭代次数必须在编译时已知。循环迭代次数是每个块的线程数和块平铺维度的函数。这两者在编译时都是固定的，因此将它们作为模板参数传递到tileMemcpy并根据这些参数计算迭代次数，并添加一个#pragma unroll即可实现。

template<unsigned int TILE_ROWS,
unsigned int TILE_COLS,
unsigned int NUM_THREADS>
__device__ __forceinline__ void tileMemcpyUnrolled(
    half* src,
    half* dst,
    const unsigned int src_stride
)
{
    // # of threads is multiple of # of columns in the tile
    static_assert(NUM_THREADS % TILE_COLS == 0);
 
    // flatten out 2d grid of threads into in order of increasing threadIdx.x
    const unsigned int thread_idx = threadIdx.y * blockDim.x + threadIdx.x;
 
    // assign each thread a row/column in the tile, calculate how many iterations we need
    // to cover the whole tile
    constexpr unsigned int ROW_STEP = NUM_THREADS / TILE_COLS;
    constexpr unsigned int NUM_ITERS = TILE_ROWS / ROW_STEP;
    unsigned int thread_row = thread_idx / TILE_COLS;
    const unsigned int thread_col = thread_idx % TILE_COLS;
 
    #pragma unroll
    for (unsigned int i = 0; i < NUM_ITERS; i++)
    {
        dst[thread_row * TILE_COLS + thread_col] =  src[thread_row * src_stride + thread_col];
        thread_row += ROW_STEP;
    }
 
}

template<unsigned int TILE_ROWS,
unsigned int TILE_COLS,
unsigned int NUM_THREADS>
__device__ __forceinline__ void tileMemcpyUnrolled(
    half* src,
    half* dst,
    const unsigned int src_stride
)
{
    // # of threads is multiple of # of columns in the tile
    static_assert(NUM_THREADS % TILE_COLS == 0);
 
    // flatten out 2d grid of threads into in order of increasing threadIdx.x
    const unsigned int thread_idx = threadIdx.y * blockDim.x + threadIdx.x;
 
    // assign each thread a row/column in the tile, calculate how many iterations we need
    // to cover the whole tile
    constexpr unsigned int ROW_STEP = NUM_THREADS / TILE_COLS;
    constexpr unsigned int NUM_ITERS = TILE_ROWS / ROW_STEP;
    unsigned int thread_row = thread_idx / TILE_COLS;
    const unsigned int thread_col = thread_idx % TILE_COLS;
 
    #pragma unroll
    for (unsigned int i = 0; i < NUM_ITERS; i++)
    {
        dst[thread_row * TILE_COLS + thread_col] =  src[thread_row * src_stride + thread_col];
        thread_row += ROW_STEP;
    }
 
}

这给我们带来了更接近以下内容的东西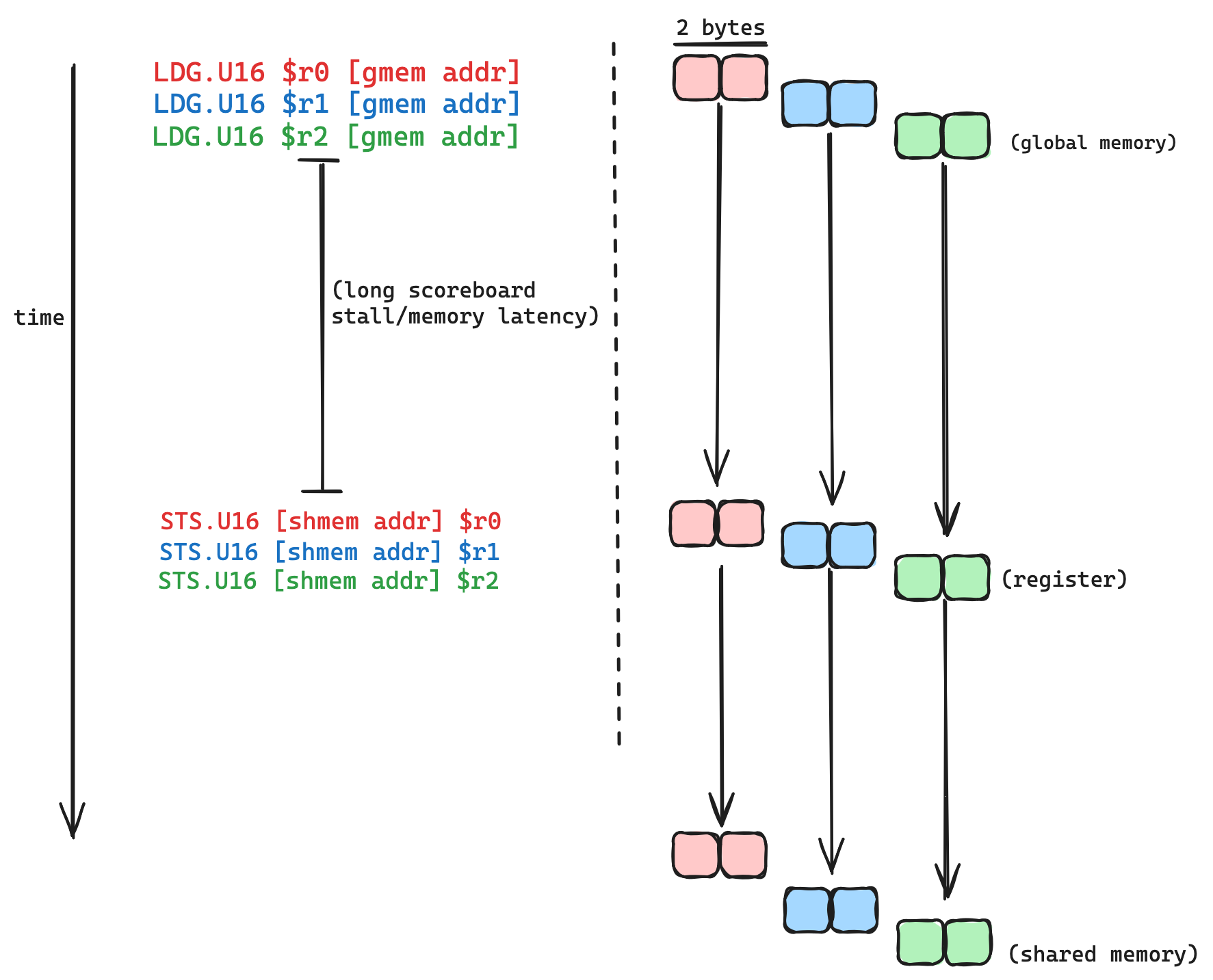： memory_latency_unrolled 在初始版本中，复制操作的总延迟大致与设备的内存延迟乘以循环迭代次数成正比。展开循环后，与第一个版本相比，总延迟应减少编译器决定相互重叠的加载数量的倍数（大致如此）。

我们在这里可以做的另一个相当简单的优化是增加每个指令加载的字节数。我们的加载操作当前编译为LDG.U16，这些指令中的每一个从 DRAM 加载 16 位/2 字节。SASS 中最宽的加载指令是LDG.128，它加载 128 位/16 字节。由于我们的内核受内存延迟而非内存带宽的限制，如果我们使用更宽的加载指令，每个内存请求将经历相同的延迟，但每次请求移动更多字节。我们将延迟分摊到更多移动的字节上，这对效率是有利的。

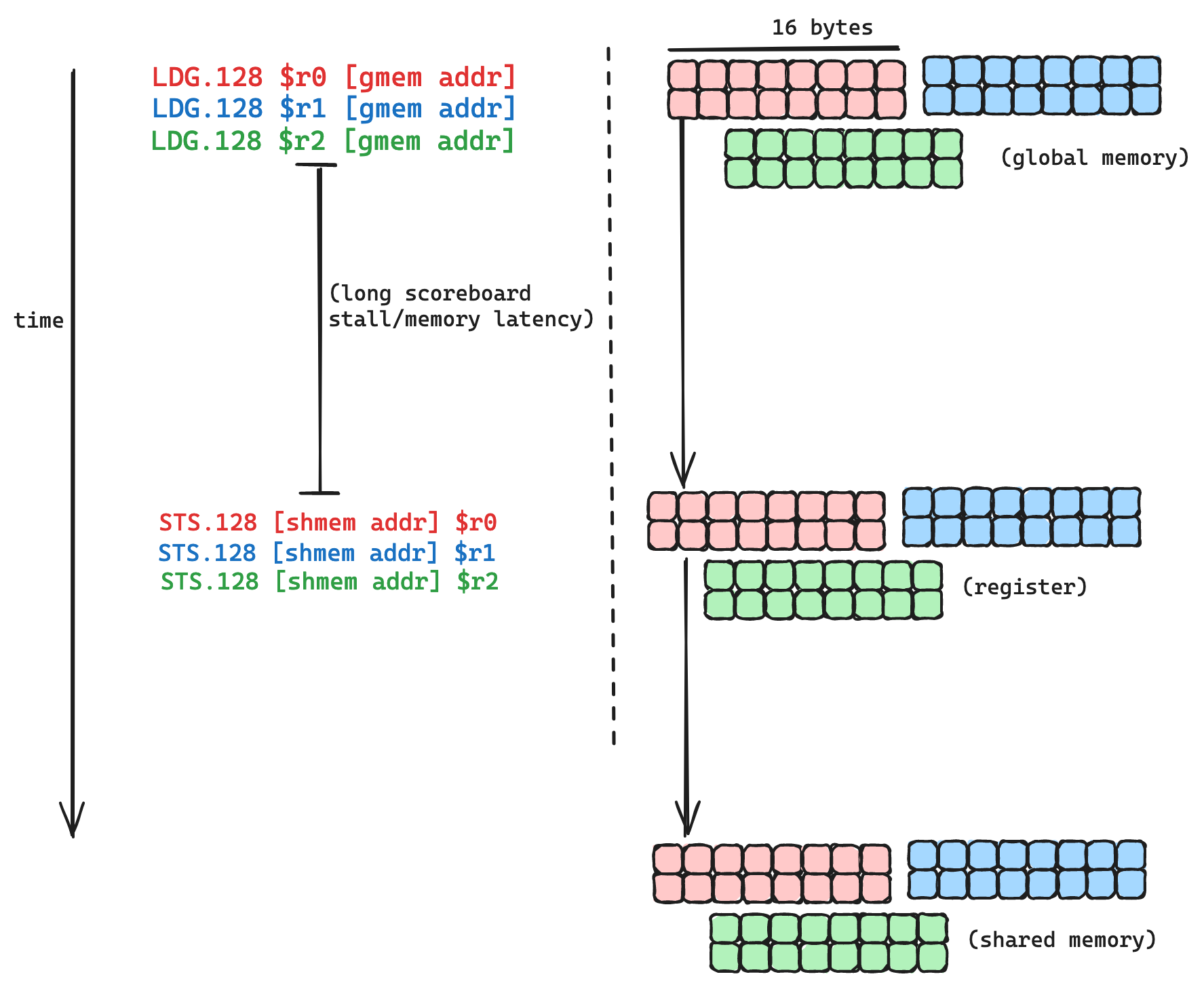
memory_latency_vectorized

实现这一点的快速而粗糙的方法是通过reinterpret_cast将src和dst指针从half转换为float4，并相应地更新索引和循环计算。这里是一个godbolt 链接指向一个具有向量化和展开内存复制的内核，这里是代码。

这些对 memcpy 的优化使吞吐量比第一个内核提高了约 3 倍。但在我们接近 cuBLAS 级别性能之前，还有很长的路要走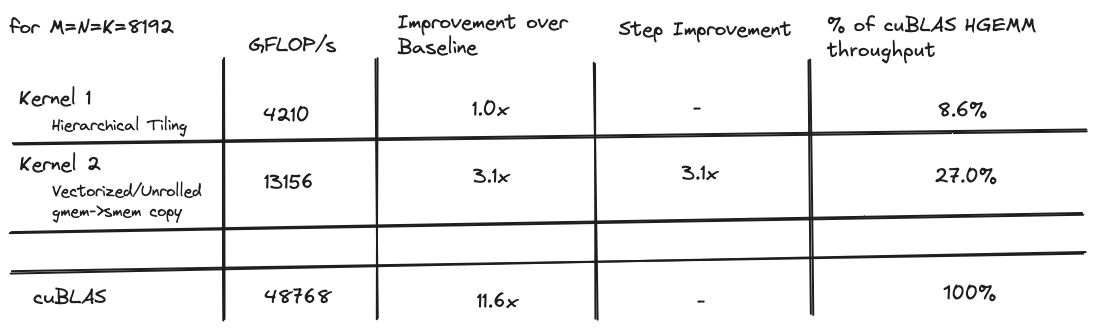 table2

内核 3 - 共享内存重排¶

回到 NSight Compute 的 warp 状态部分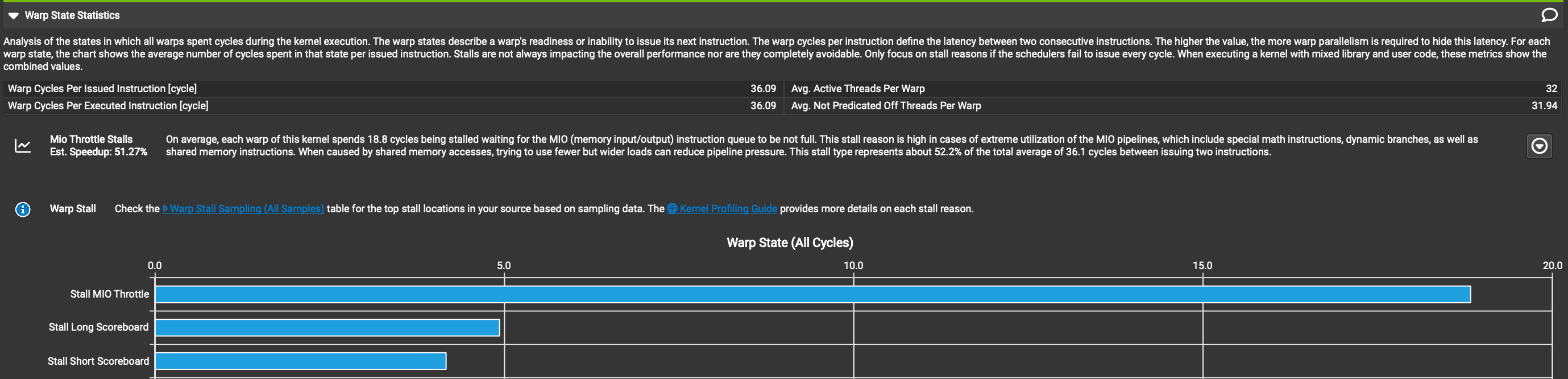 kernel2_nsight_compute 长记分板停顿不再是 warp 停顿的主要问题，我们的内核在应用了上一节描述的优化后性能提高了约 3 倍。Warp 现在平均每个发出的指令因称为“MIO 节流”的原因而停顿约 19 个周期。什么是 MIO 节流，我们如何解决它？根据 nsight compute文档这意味着：

Warp 因等待 MIO（内存输入/输出）指令队列不满而停顿。在 MIO 管道（包括特殊数学指令、动态分支以及共享内存指令）极端利用的情况下，此停顿原因较高。

在我们的情况下，这种停顿几乎肯定是由共享内存指令引起的，因为我们的内核动态分支很少，并且没有三角函数或任何其他特殊数学指令。具体来说，这是由于共享内存 bank 冲突。根据这里共享内存 bank 冲突的两个症状是非常高的 L1/TEX 吞吐量数字（当前为峰值的 97%）和 MIO 节流停顿，这些都是共享内存 bank 冲突的次要影响。我了解到，如果你的内核性能因共享内存 bank 冲突而受损，这在查看 NSight Compute 时并不明显，但信息确实存在。我发现，为了查看共享内存 bank 冲突发生的位置并理解其严重性，我必须学习“wavefront”的术语。为了理解这个术语，需要一些关于共享内存的背景知识。

背景：Bank 冲突和 Wavefronts¶

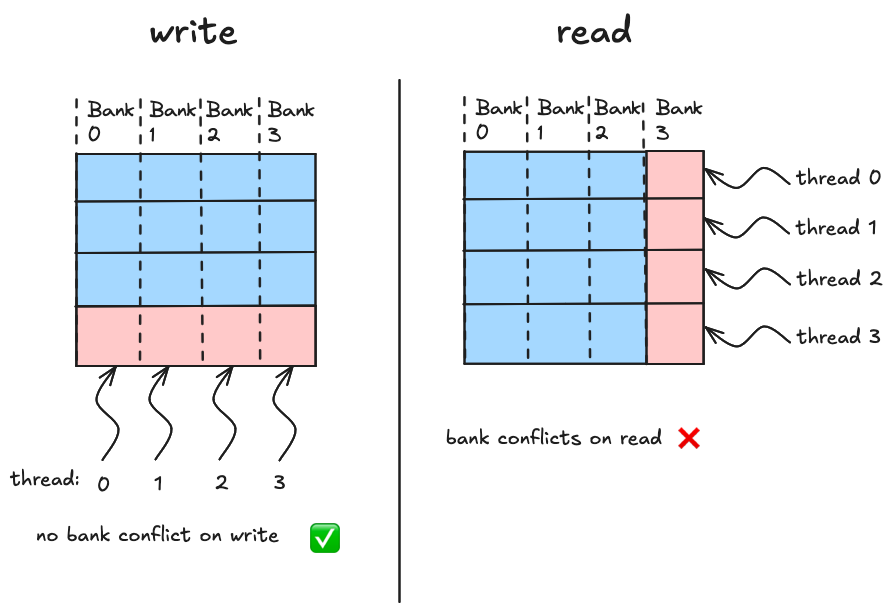
从 CUDA 程序的角度来看，共享内存的工作原理如下（这里是官方指南）。如果你在内核中声明一个__shared__数组，它对应于位于特定流多处理器上的物理内存。因此，这个数组访问速度快，但只能由 SM 上的线程访问，用 CUDA 的语言来说，这意味着共享内存数组是特定线程块本地的。物理上，内存分布在 32 个“banks”之间，每个 bank 存储相邻的 4 个字节，如下所示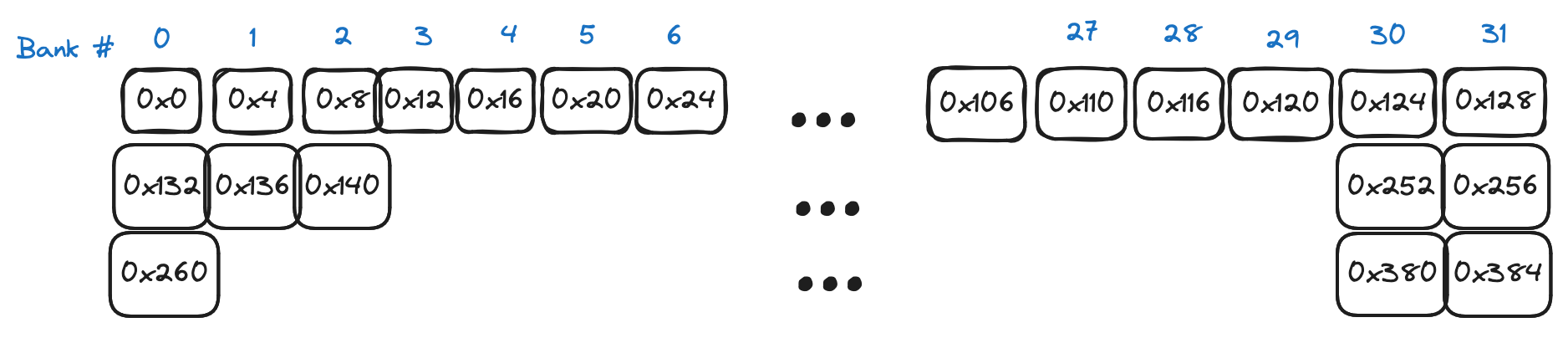： shmem_1 每个 bank 每个时钟周期可以产生一个 4 字节的值。如果我们的目标是最大化从共享内存的读写带宽，我们在决定访问模式时需要记住这一点。当 warp 中的 32 个线程将它们的访问均匀分布在 32 个 banks 上时，实现全带宽。Bank“冲突”发生在单个 bank 必须为给定请求为多个线程产生数据时。为了展示 bank 冲突和 wavefronts 的概念如何联系在一起，这里有 3 个场景，都在一个简化的世界中，我们有 4 个线程和 4 个内存 banks 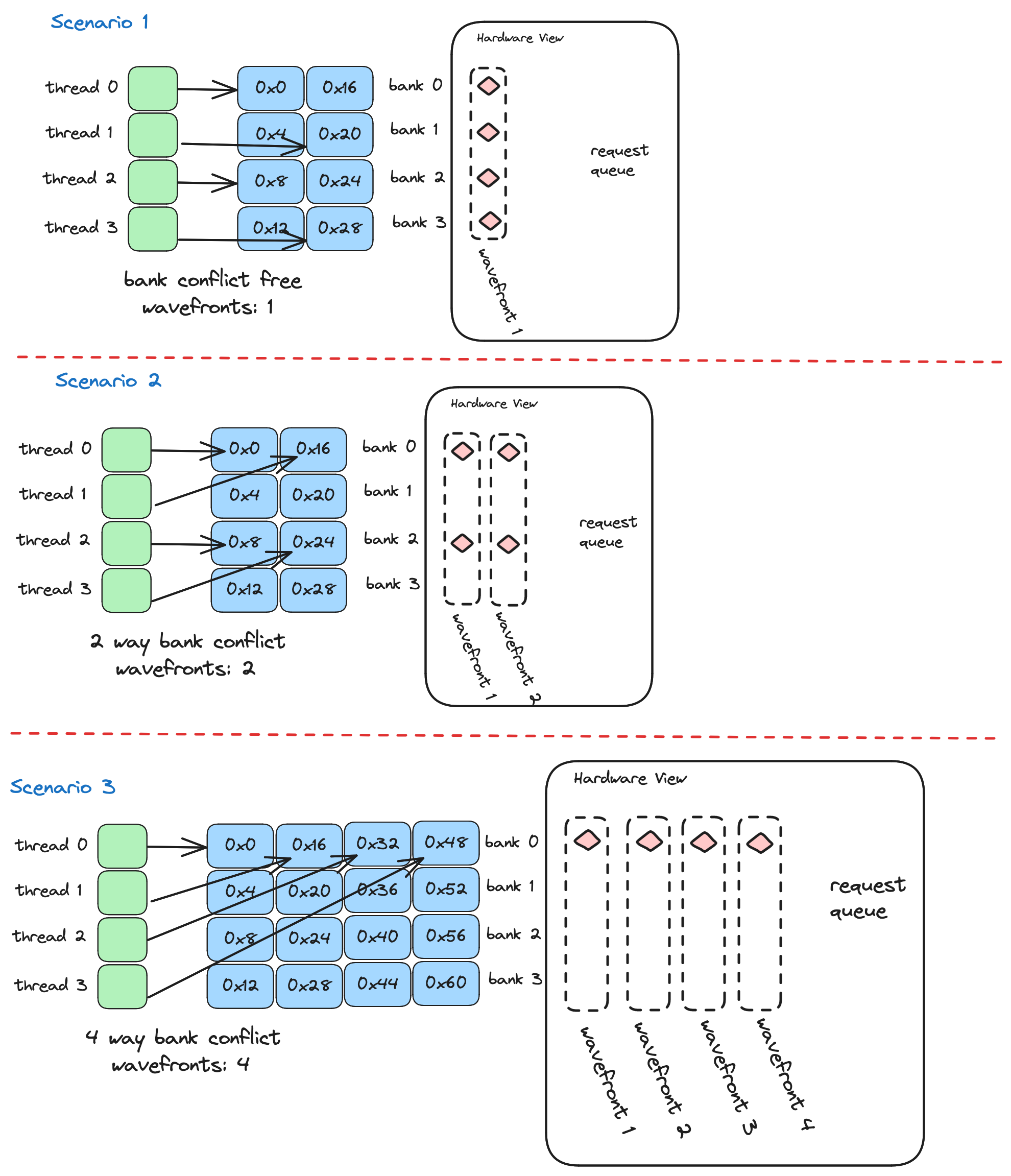bank_conflicts 当从共享内存加载或存储时，每个线程请求一个特定的内存地址，在我们的简化世界中，该地址落入四个内存 banks 之一。在场景一中，每个线程访问不同 bank 中的数据，硬件计算这四次访问可以合并为硬件处理的单个事务，这个词是wavefront。在场景二中，四个线程访问落入四个 banks 中两个的地址。由于每个 bank 一次只能发送一个字，硬件将这四次请求分组为两个 wavefronts，内存硬件一个接一个地处理这两个 wavefronts。场景三是最坏情况，四个线程访问全部落入第 0 个内存 bank 的地址，在这种情况下，需要四个独立的 wavefronts 来服务这四个线程的事务。

对于四个线程访问四个字节的情况，“理想”的波前数量为一，因为（理想情况下）无论哪些线程访问哪些字节，我们都应该能够安排数据，使得所有访问均匀分布在各个存储体中。例如，所示场景三不够理想，但我们可以通过转置共享内存中的字节来使其理想化，这将导致四次访问均匀分布在四个存储体上。但对于所示布局，实际的波前数量为四。

NSight Compute 将告诉我们每次内存访问：

理想的波前数量
实际的波前数量
过量的波前数量，即 2 - 1

根据以上分析，如果我们的代码存在 n 路存储体冲突，n 应等于实际波前数量除以理想波前数量。我们希望实际等于理想，这通常需要仔细思考数据的布局方式以及线程如何访问它。

ldmatrix 存储体冲突¶

以下是 NSight Compute 中每条指令的实际/理想波前截图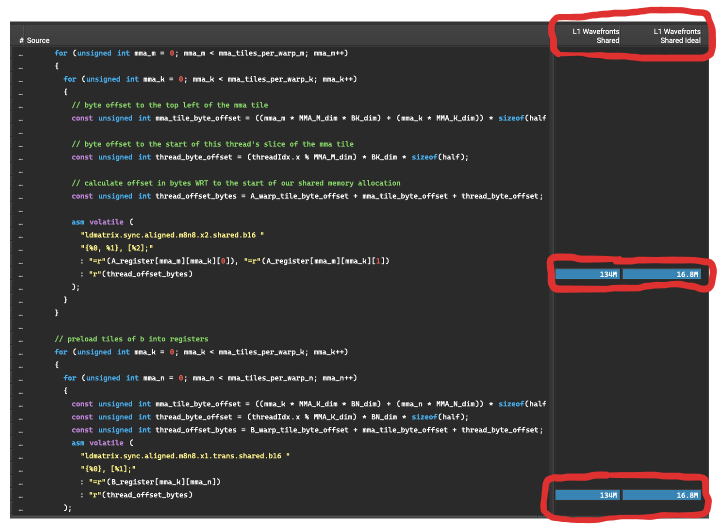： l1_wavefronts_source_view 这些ldmatrix命令正在将数据从共享内存加载到线程本地寄存器内存中，为 MMA 操作做准备。NSight Compute 告诉我们实际与理想的比率约为 8 左右，这表明此内存访问导致 8 路存储体冲突。为了制定修复此性能杀手（performance killer）的策略，我们需要理解其发生原因。

在 Kernel 1 所示的平铺结构中，在 warp 循环（绿色部分）的每次迭代中，单个 warp 负责从共享内存读取一个 64x64 的数据块，并将其写入寄存器。共享内存读取是发生存储体冲突的地方。在下面的可视化中，顶部是这些 64x64 块之一的非常缩小的版本，跨存储体的布局通过列的颜色可视化。我们可以看到，一行 64 个元素，每个元素 2 字节，很好地跨越了 32 个存储体。底部是一个 8x8 块的放大版本，该块通过ldmatrix从共享内存带入寄存器。每个 warp 以 8x8 的增量迭代其本地 64x64 块，在每个小块上调用ldmatrix，此 PTX 指令从共享内存加载值，并在 warp 内的寄存器之间混洗加载的数据，以匹配张量核心指令期望的寄存器布局。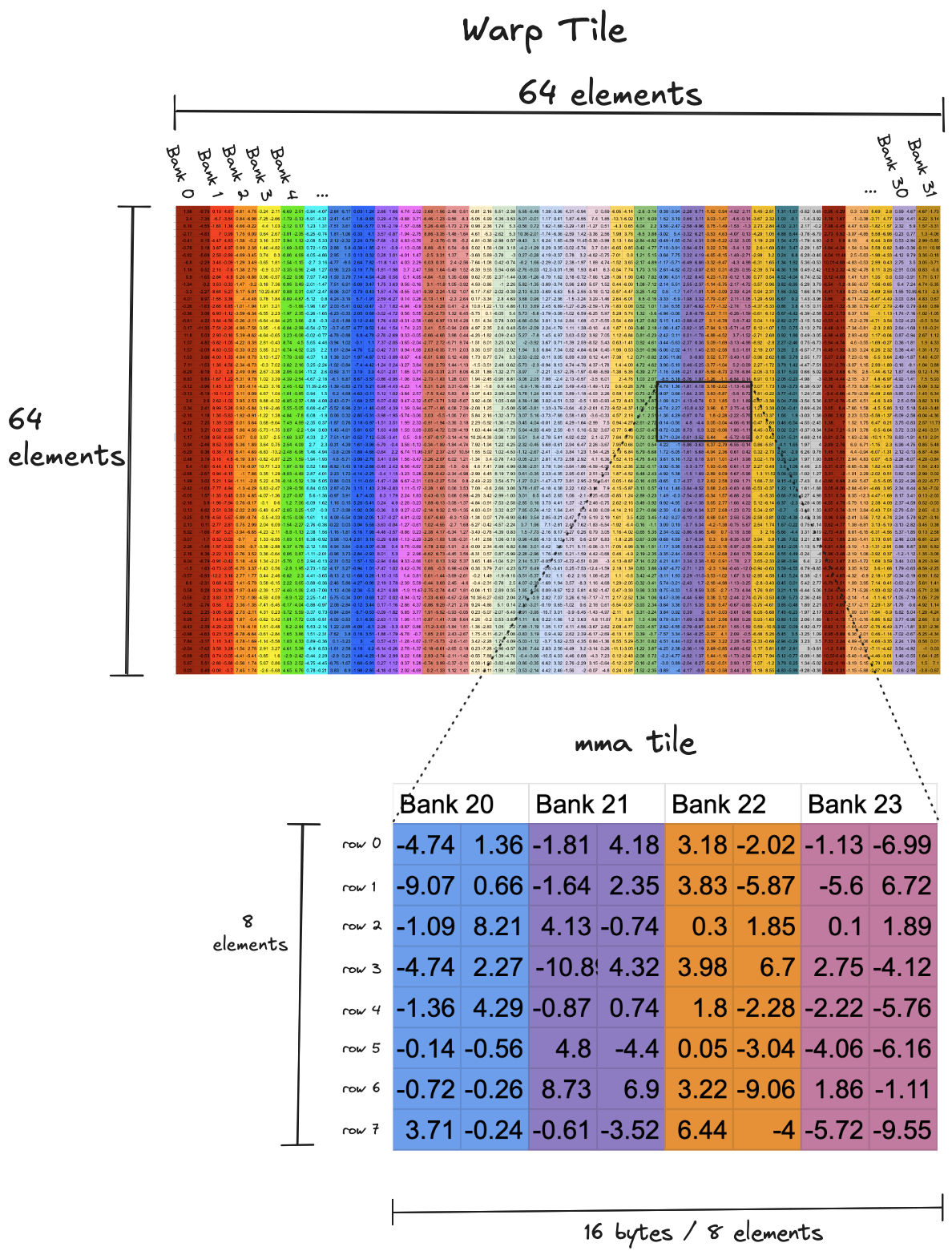 mma_tile_zoom_in 的内部工作机制有些不透明，它编译为单个 SASS 指令ldmatrix，而不是多个显式的共享内存加载和寄存器混洗，正如人们可能期望的那样。然而，我们不需要理解LDSM...的内部工作机制来理解为什么每次调用它时会发生 8 路存储体冲突。相反，8 路存储体冲突是每个给定块中的行分布在相同四个存储体上的必然结果。读取每行需要一个波前，共有八行，这意味着八个波前。理想情况下，如果每个块中的八行均匀分布在三十二个存储体上，整个块可以用单个波前读取。读取这些块是内核的内循环，对于 8192x8192 的操作数，我们总共读取 (8192/8)³ = 1,073,741,824 个这些块，这相当于大量的存储体冲突。因此，如果我们关心性能，值得花时间修复它。ldmatrix的内部工作机制来理解为什么每次调用它时会发生 8 路存储体冲突。相反，8 路存储体冲突是每个给定块中的行分布在相同四个存储体上的必然结果。读取每行需要一个波前，共有八行，这意味着八个波前。理想情况下，如果每个块中的八行均匀分布在三十二个存储体上，整个块可以用单个波前读取。读取这些块是内核的内循环，对于 8192x8192 的操作数，我们总共读取 (8192/8)³ = 1,073,741,824 个这些块，这相当于大量的存储体冲突。因此，如果我们关心性能，值得花时间修复它。

填充¶

为了拥有无存储体冲突的内核，我们需要重新排列共享内存中的数据布局，以便我们可以在没有任何过量波前的情况下读取和写入共享内存。挑战在于共享内存读取的线程到数据映射与共享内存写入的不同。写入时，相邻线程写入行中的相邻值，而读取时相邻线程读取列中的相邻值。

row_vs_column_shmem_access

这是使用 2D 共享内存块的内核中的常见情况，标准修复方法是在共享内存数组的每行末尾添加一些填充（即空空间）。如果我们以这样的方式添加填充，使得数组的单行不再完美地适应 32 个存储体，列中的相邻值就不再落入同一存储体，这意味着我们可以读取列而没有任何过量波前。这在图片中比在文字中更清晰，这里再次是一个简化案例：一个迷你数组（4 列和 4 行）存储在一个只有 4 个存储体的迷你 GPU 上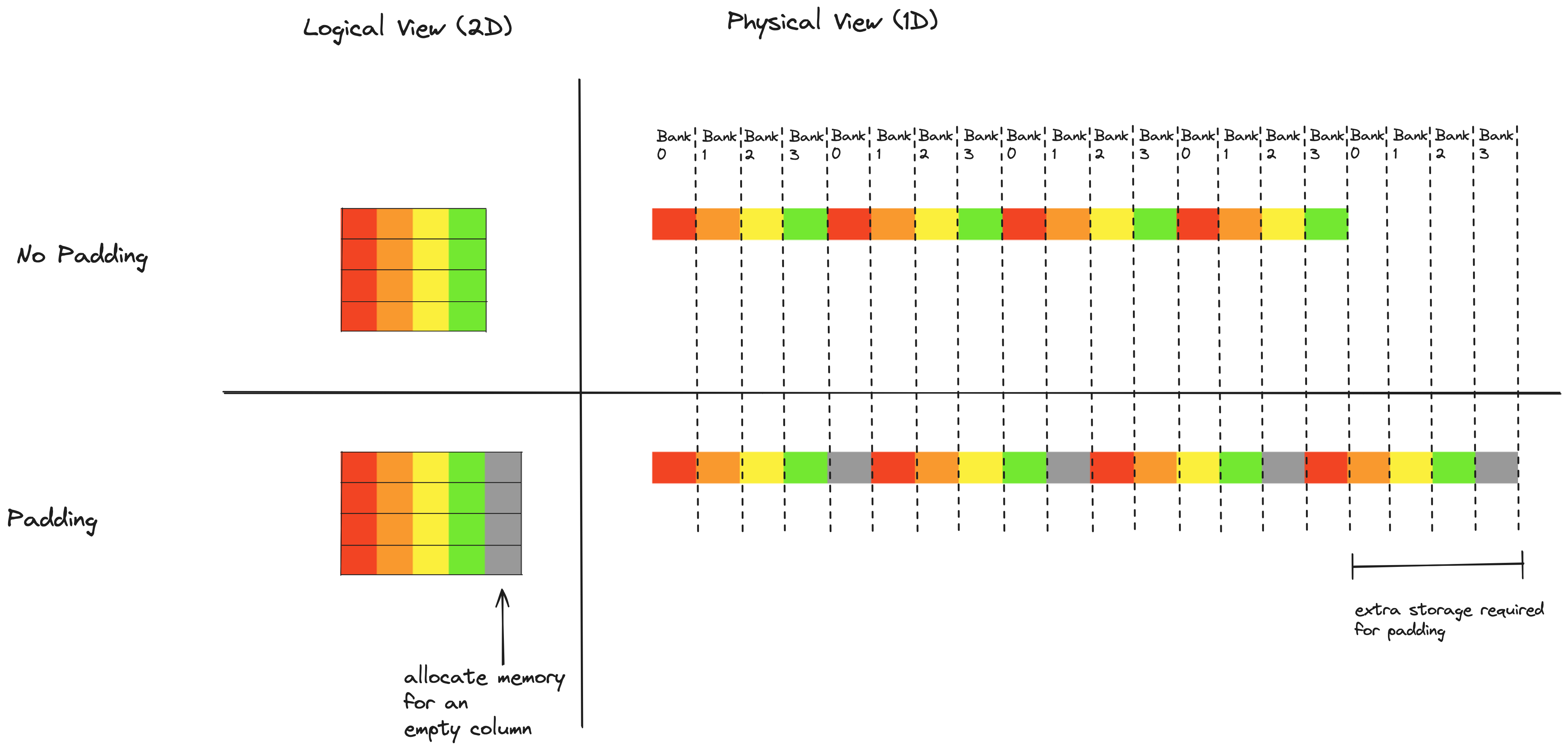： simple_smem_padding 数组元素按列颜色编码。注意，在无填充情况下，给定列中的所有数组元素落入同一存储体。添加填充列后，给定列中的数组元素分布在所有 4 个存储体上。填充技术可以在这里用于完全消除存储体冲突。由于我们使用向量化写入共享内存，我们每次以 16 字节块写入共享内存，每个块必须对齐。向共享内存的每行添加 16 字节填充将导致每个 8x8 MMA 块分布在所有 32 个存储体上（说服自己这一点的练习留给读者）。

使用填充技术的缺点在于它要求我们在共享内存中分配额外的、未使用的空间。在 Kernel 2 中，A 的共享内存图块为 256x64，B 的共享内存图块为 128x64。如果我们为两者都添加一个额外的 16 字节（即 8 个元素）列，这将使分配的共享内存量增加 25%，总计增加 6144 字节。这种浪费的空间被证明是一个显著的缺点，因为在编写高性能内核时，共享内存是非常宝贵的资源——这一点在使用称为双缓冲的技术时尤其明显，未来内核中的每个线程块最终将在每个 SM 上使用 65536 字节共享内存的 100%。因此，我们应该思考是否有办法在不浪费任何共享内存空间的情况下消除存储体冲突。事实证明，这是非常可能的！

Swizzling（玩具示例）¶

Swizzling 可能是我在这个工作过程中学到的最喜欢的技术。单词“swizzle”有几种不同的用法，在鸡尾酒的语境中它意味着stir，而在 GPU 的语境中它意味着rearrange。在我们消除 2D 数据图块中共享内存存储体冲突的上下文中，swizzling 意味着对共享内存图块内的元素进行排列，使得我们可以在没有任何存储体冲突的情况下访问数据。这是那些对我来说看起来像黑魔法一样的技术之一，直到我花时间去理解它，现在我欣赏它的巧妙和优雅。

在我们的 4x4 图块中，我们添加填充是因为它以理想的方式改变了数据和存储体之间的对齐。Swizzling 基于这样的观察：我们不需要额外的填充字节来将列元素均匀地分布在存储体上。相反，我们可以直接找出一种矩阵元素的排列方式，以正确的方式分散列，并在写入共享内存时应用这种排列。这里是一个“swizzle”的图示，即一种可以消除存储体冲突的元素排列。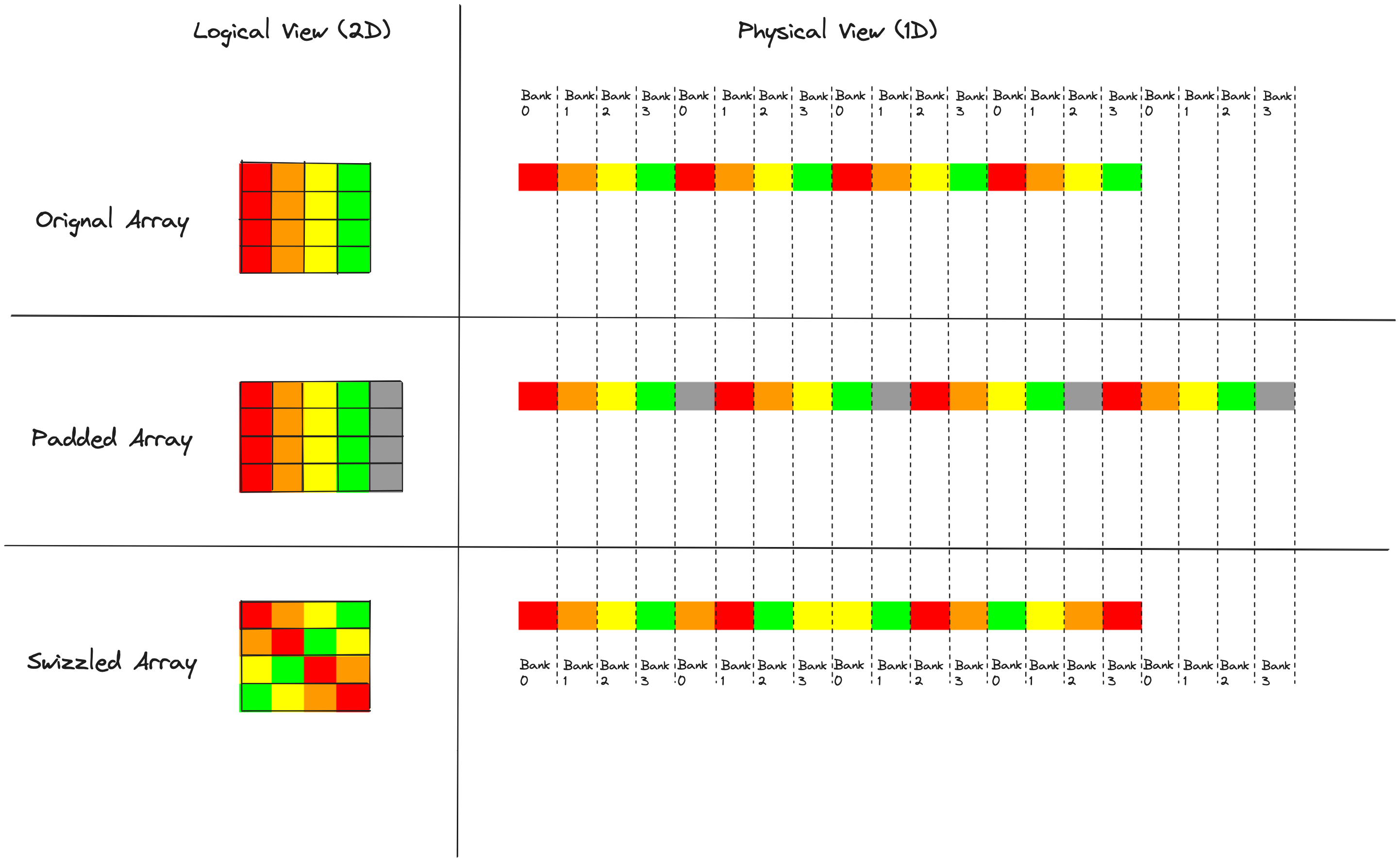 simple_smem_swizzled 此时值得记住的是，我们的共享内存布局必须满足两个要求：写入时无存储体冲突的行访问，以及读取时无存储体冲突的列访问。

在所有三种情况下，每一行在内存中都是连续的，并且分布在所有四个存储体上，这意味着每一行都可以在没有任何存储体冲突的情况下写入。这里的观察是，当我们应用排列或“swizzle”时，我们不希望跨行排列元素，只希望在行内排列；否则我们可能会失去无存储体冲突写入的这一特性。

促使我们思考共享内存布局的问题是读取列时发生的存储体冲突。添加填充在这里修复了存储体冲突，但代价是浪费共享内存。Swizzling 给了我们两全其美的方案；我们可以在没有存储体冲突的情况下读取列，并且没有共享内存被浪费。那么我们如何考虑应用这种排列呢？

上面显示的 swizzle 可以实现为一个函数f，它将索引映射到新索引。如果A是原始数组，A_s是 swizzled 数组，i是元素的索引，那么A_s[f(i)] = A[i]。那么这里的f是什么？

由于f操作的是数组索引，我们应该思考这些索引可以表示和查看的不同方式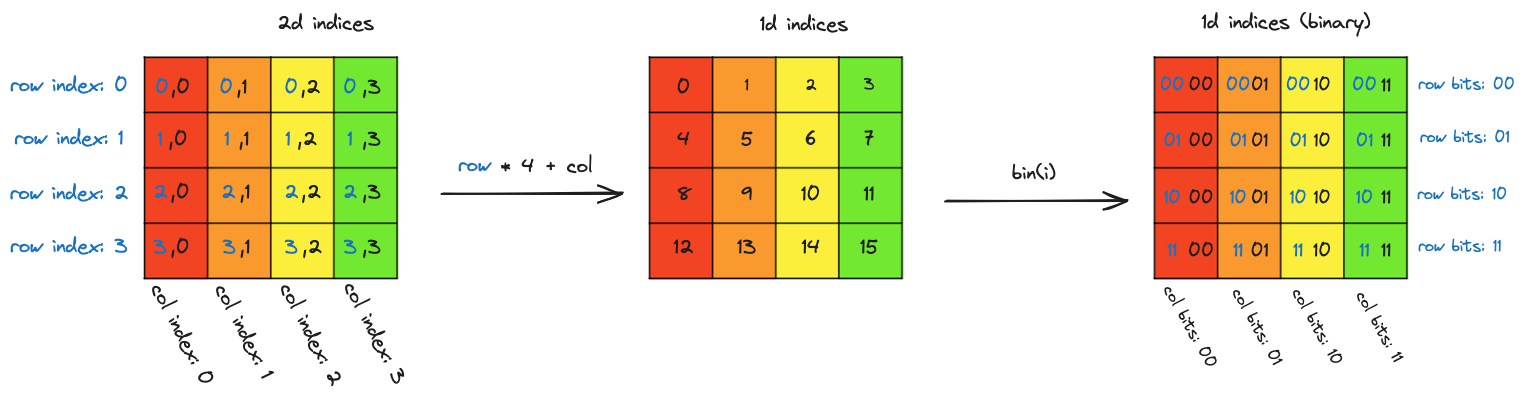： simple_smem_indices 最左边是 2D 行和列索引。移到中间，这些索引可以线性化为数组中 16 个元素的顺序（在这种情况下是行优先）排序。移到右边，当我们以二进制查看顺序索引时，可以看到 2D 结构存在于索引位中。索引中的两个最低有效位编码列，另外两个位编码行。作为剧透，f将从右侧的视角操作，即扁平数组索引的二进制表示。以下是关于f需要做什么的两个观察：

为了避免写入时的存储体冲突，我们希望在一行内排列元素，换句话说，没有元素应该切换行。这意味着f应该修改编码列的位，而保持编码行的位不变。
我们希望为每一行应用不同的排列，并且对于任何给定的列，我们希望该列中的元素在 swizzled 数组中分布在所有四列上。

我们可以使用 XOR 函数来实现这两个目标，具体来说，通过将每个元素的行位与其列位进行 XOR，并将结果用作新的行位。这是一个逐行的分解，展示了 XOR 列位与行位如何在行内移动值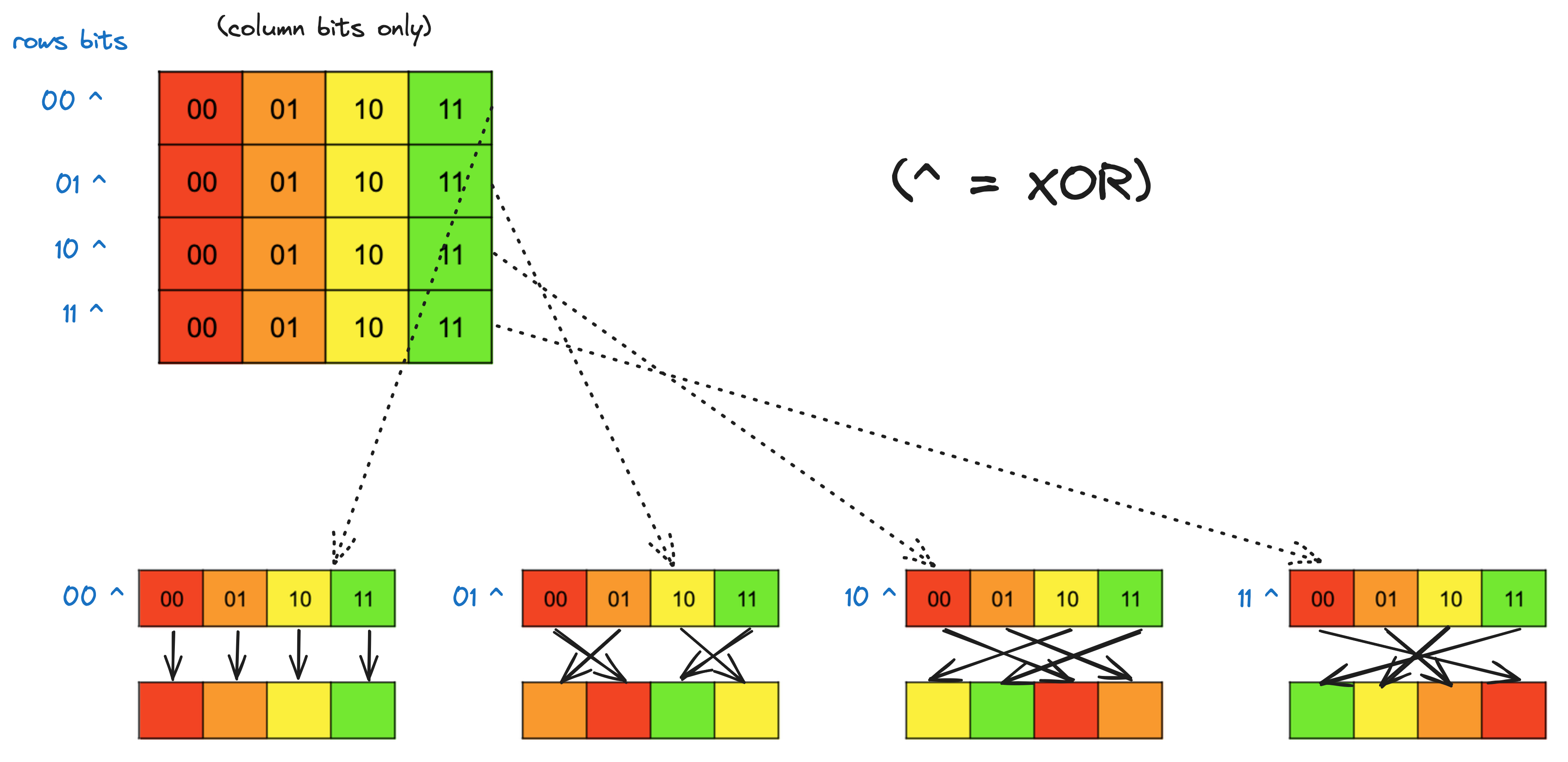： swizzled_rows 为我们做这件事的f是f(i) = i ^ ((i & 0b1100) >> 2)。掩码从i中选择两个列位，然后将这两个位右移两位，使它们与i的两个行位对齐，然后我们进行 XOR。i的列位保持不变。

这是对所有行一起应用此函数结果的可视化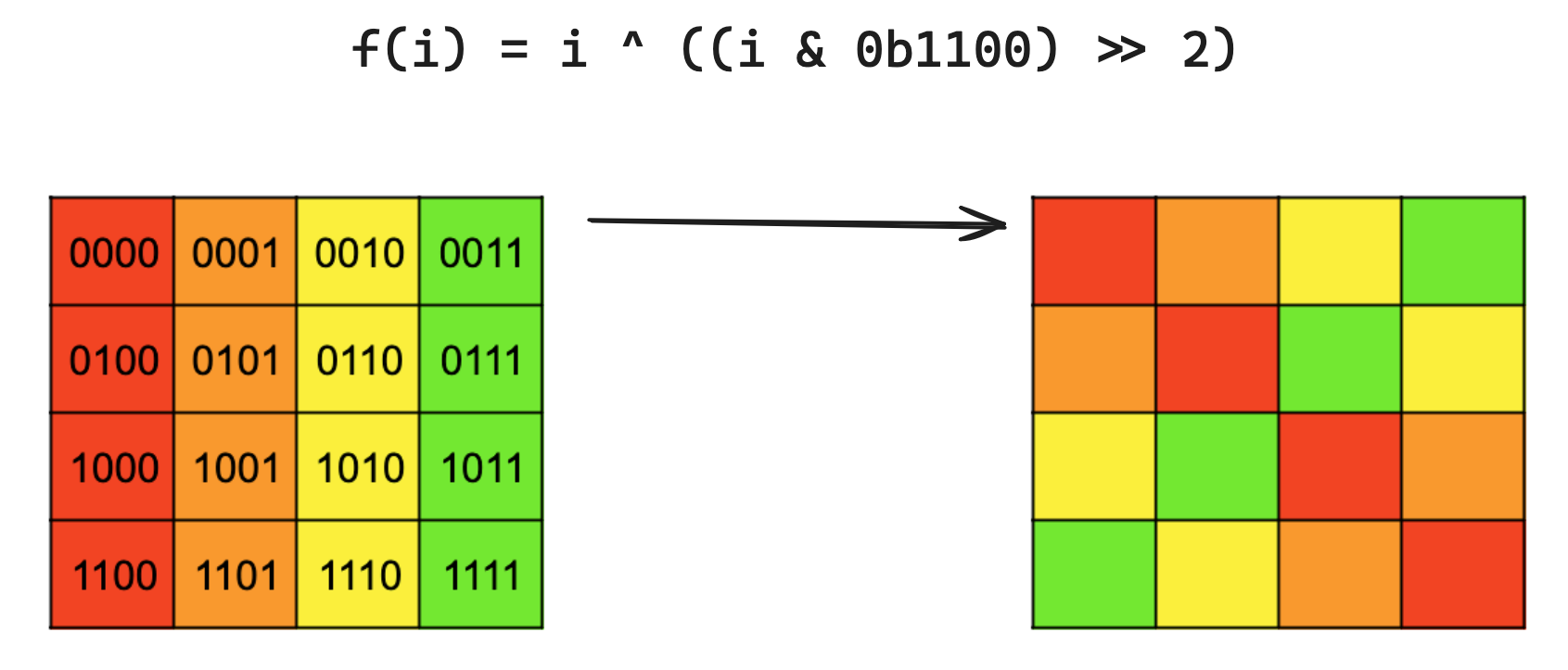： 2d-swizzle

Swizzling（实际应用）¶

现在我们需要弄清楚如何使用这种技术来排列我们的共享内存布局，使得我们可以用 0 个额外的波前读取单个 8x8 mma 图块。提醒一下，这是我们共享内存布局的视图，其中突出显示了一个感兴趣的图块。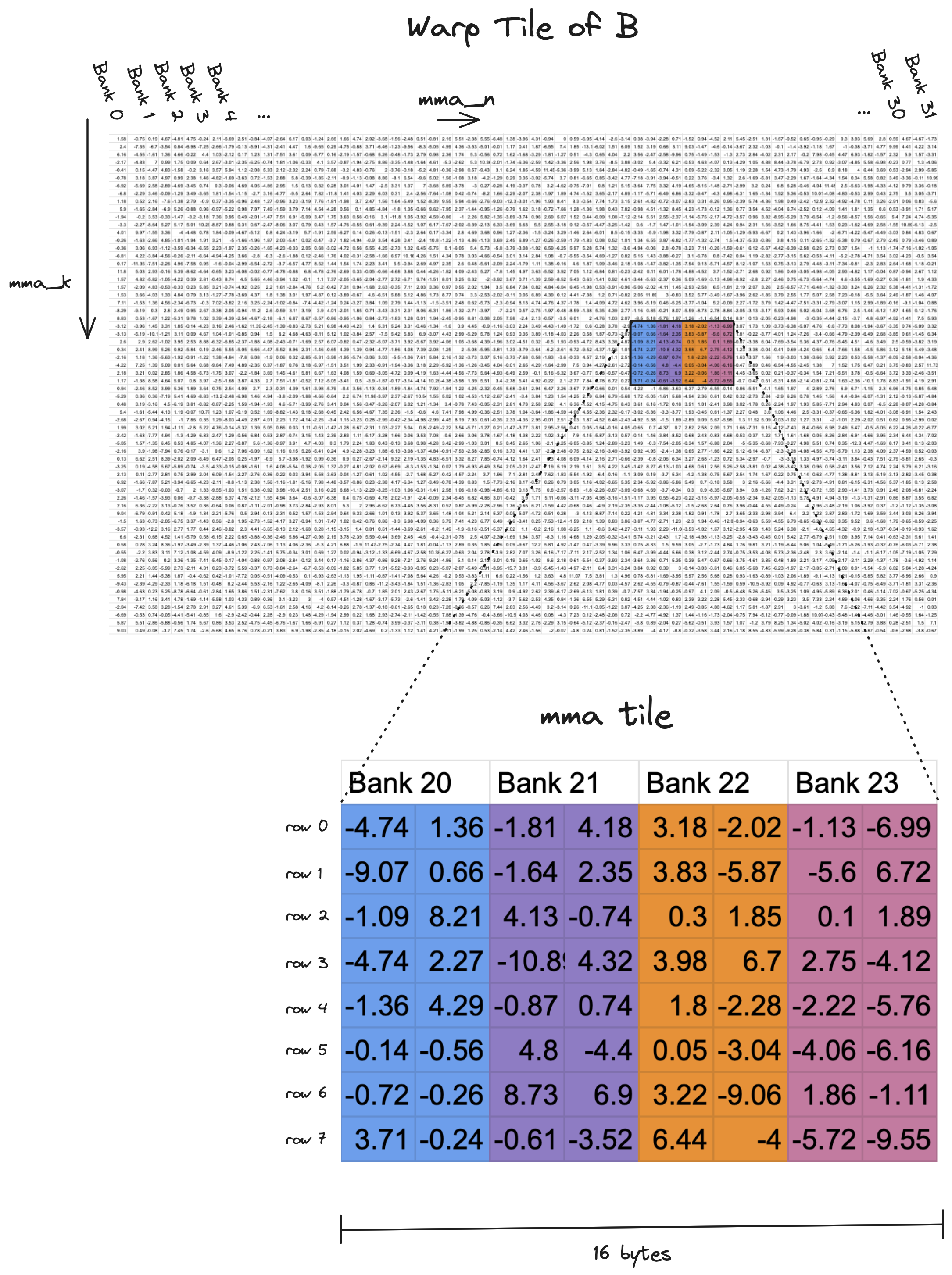 mma_tile_zoom_in_blank

我们的目标是找出一个 swizzle 函数，将这个图块中的 8 行分布在所有 32 个存储体上，而不是像上面那样将所有 8 行塞进 4 个存储体中。从完整图块的视图来看，上面图块的行将像这样分布。

mma_tile_zoom_in_swizzle

为了弄清楚我们应该使用什么 swizzle 函数，让我们看看这个图块索引的二进制表示，并为其分配一些对应于我们平铺方案的结构。

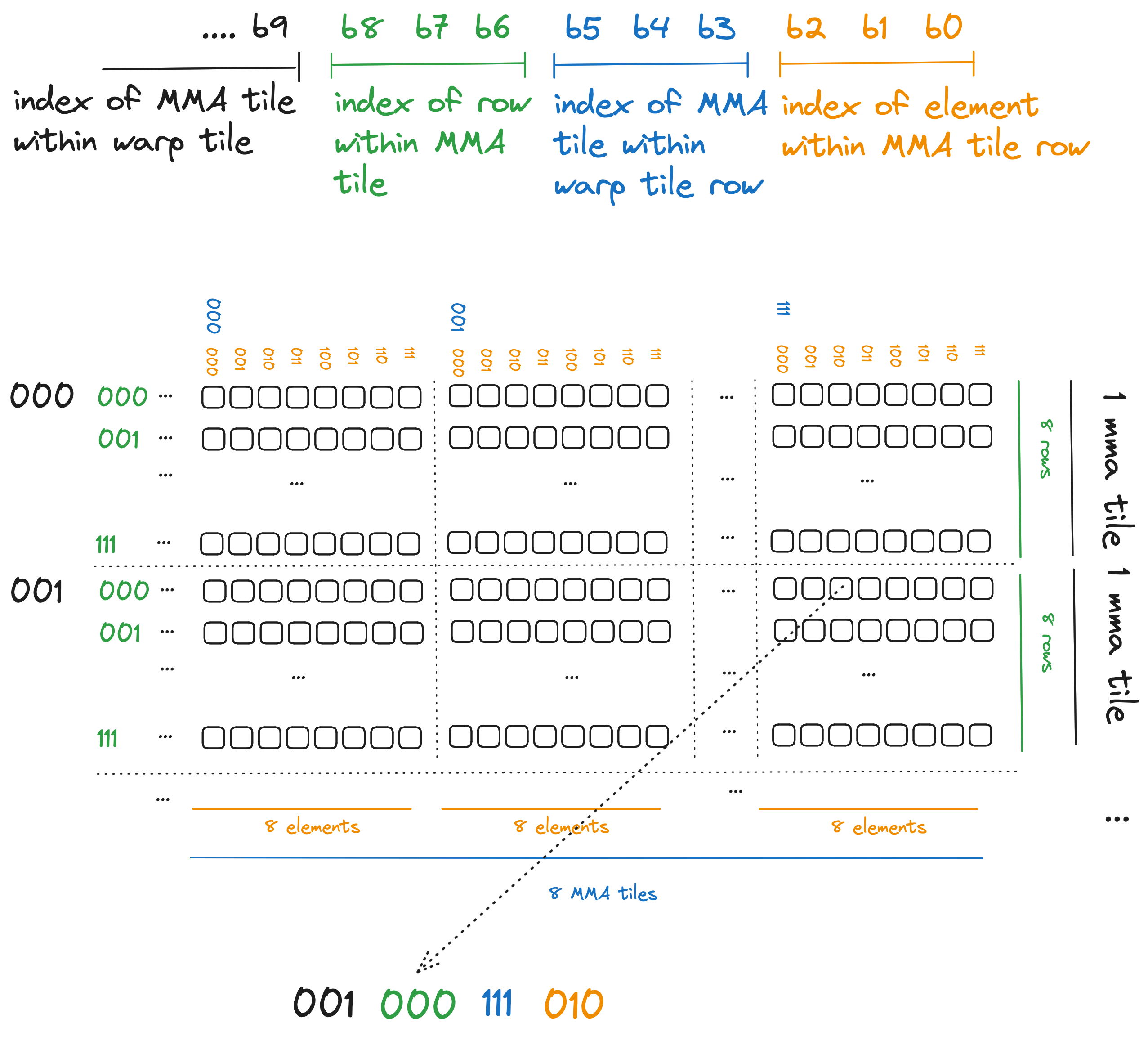
swizzle_index_groups

关于我们的 swizzling 函数应该做什么和不应该做什么的一些说明：

我们希望保持每个 MMA 瓦片行中的八个元素在一起。换句话说，当我们应用交换（swizzle）时，8x8 MMA 瓦片单行中的八个相邻元素将保持在一起。这意味着我们的交换函数不会触及橙色位。
发生存储体冲突（bank conflicts）是因为 MMA 瓦片内的 8 行完美地堆叠在一起。在 MMA 瓦片内，我们希望将这 8 行水平展开到整个 warp 瓦片中。蓝色位编码每个 MMA 瓦片在 64 元素宽的 warp 瓦片中的位置，因此这些蓝色位是我们希望交换函数修改的部分。
我们不希望移动行之间的元素，因此我们的交换函数不会修改绿色行位。然而，这些绿色行位提供了一个很好的交替模式，我们可以将其与蓝色位进行 XOR 运算，以在其行内混合 MMA 瓦片。
再次强调，我们不希望移动行之间的元素，而黑色位（图中显示的最高有效位）编码每个 MMA 瓦片的起始行。我们的交换函数将忽略它们。

因此，这一切意味着对于每个索引，我们希望取蓝色位，将其与绿色位进行 XOR 运算，并用 XOR 的结果替换原始的蓝色位。如果i是我们想要交换的索引，这可以表示为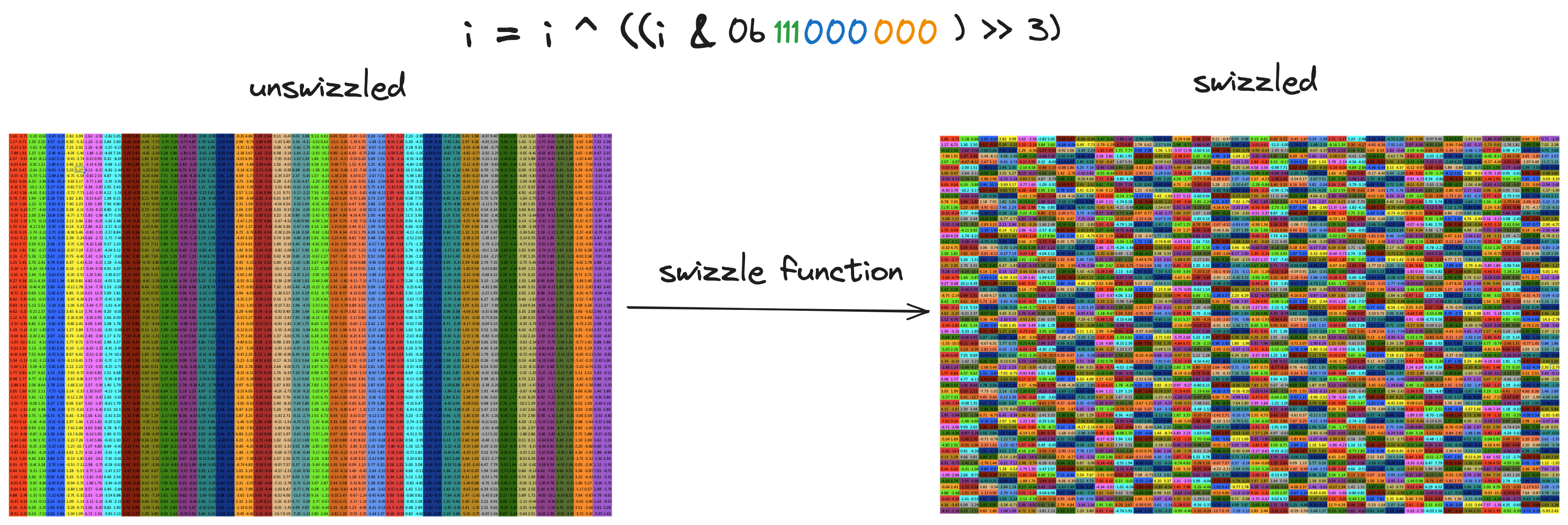： swizzled_vs_unswizzled 就这样，我们消除了存储体冲突。交换比填充技术需要更多思考，交换函数的选择取决于共享内存数组的维度和我们用于读/写的向量宽度（即float4、float2、int等）。因此，如果我们使用交换，每次考虑更改这些参数时都需要额外考虑。但如果你想消除存储体冲突，又不想增加共享内存占用，交换就变得必要。我认为这非常优雅和巧妙，如果你比较内核 2 和内核 3，总共只有约 4 行代码发生变化，这四行是在共享内存索引计算中添加了交换。

我通过查看 CUTLASS 仓库中实现的Swizzle类here弄清楚了这一切。通过其三个参数bits、base和shift，这个类代表了一系列交换函数，这些函数对数组索引的位进行移位和 XOR 运算。我还见过更奇特的交换函数示例（参见幻灯片 27here），这些超出了 CUTLASS 中实现的范围。我发现可视化不同交换函数应用的排列很有帮助，为此我写了一些 Pythoncode来美化打印数组、应用交换函数并计算存储体冲突。

消除存储体冲突带来了约 2 倍的加速，并使我们的吞吐量达到约 cuBLAS 水平的 50%。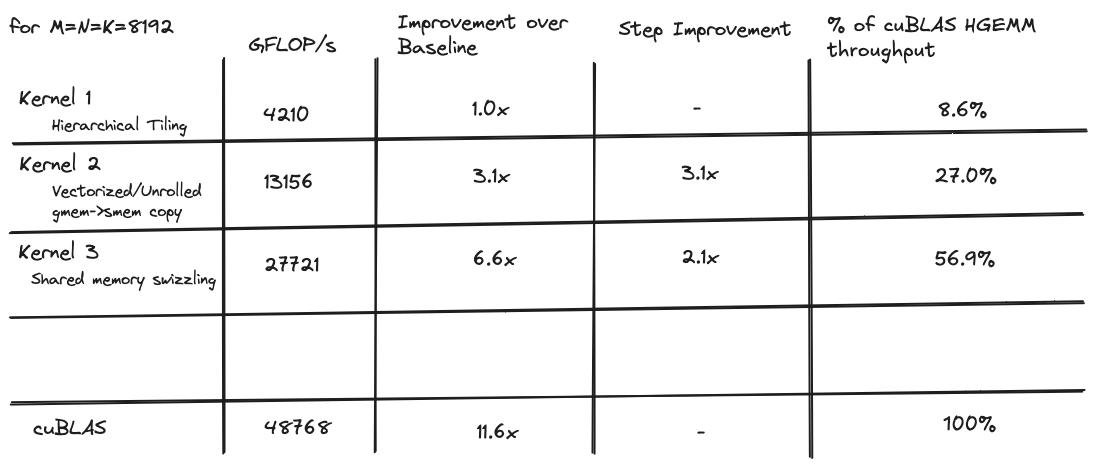 table3

内核 4 - 临时异步复制¶

每个优化都针对前一个内核中性能最差的部分。应用每个优化后，如果有效，内核中性能最差的部分应该会改变。在修复共享内存存储体冲突之前，内循环中的共享内存操作是瓶颈。消除存储体冲突后，内循环变得更加高效，瓶颈再次变为全局内存到共享内存传输的延迟。这在内核 2中通过向量化和循环展开得到了解决，但在修复存储体冲突后，NSight Compute 告诉我们这里有更多延迟需要隐藏。以下是当前循环嵌套的伪代码，以及需要改进的代码的放大视图： long_scoreboard_stall_kernel3 问题再次出现在执行全局内存到共享内存复制的行：

dst_float4[dst_index] = src_float4[src_index];
// shared memory        // global memory

dst_float4[dst_index] = src_float4[src_index];
// shared memory        // global memory

从硬件的角度来看，这是一个阻塞操作，因为当给定线程执行生成的汇编代码时，线程将在数据从全局内存到达的整个过程中停滞。上述行等价于：

float4 tmp = src_float4[src_index]; // global memory to register
dst_float4[dst_index] =  tmp; // register to shared memory

float4 tmp = src_float4[src_index]; // global memory to register
dst_float4[dst_index] =  tmp; // register to shared memory

全局内存到寄存器的传输（第一行）会产生延迟，因为数据来自片外。当需要从寄存器存储到共享内存（第二行）时，硬件检测到从全局内存所需的数据尚未到达tmp，执行会停滞直到数据到达。在内核 2中，我们通过分摊每次事务移动更多数据的延迟（向量化）和帮助编译器交错多个加载/存储（循环展开）来解决这个性能问题。但 NSight Compute 告诉我们，即使在这些优化之后，这种停滞（特别是这一行）仍占内核总停滞时钟周期的约 20%。

这里的关键观察是，如果我们将dst[...] = src[...]行分解为其两个组成部分，我们可以将它们分开，以便在数据从全局内存传输时执行其他有用工作。总体思路是，我们可以将数据从全局内存预取到寄存器存储中，比当前计算的block_k提前一个block_k。在非常高的层次上，我们希望从这样：

float4 tmp = src_float4[src_index]; // global memory to register
// (stall while we wait for data to arrive from memory)
dst_float4[dst_index] =  tmp; // register to shared memory
{
    // compute inner loop for current block tile
}

float4 tmp = src_float4[src_index]; // global memory to register
// (stall while we wait for data to arrive from memory)
dst_float4[dst_index] =  tmp; // register to shared memory
{
    // compute inner loop for current block tile
}

变成这样：

float4 tmp = src_float4[src_index]; // global memory to register
{
    // compute inner loop for previous block tile
}
dst_float4[dst_index] =  tmp; // register to shared memory

float4 tmp = src_float4[src_index]; // global memory to register
{
    // compute inner loop for previous block tile
}
dst_float4[dst_index] =  tmp; // register to shared memory

这里的关键改进是，我们启动对应于block_k的全局内存数据加载，并同时执行对应于block_k-1 的计算。通过这样做，我们用对应于block_k-1 瓦片的计算隐藏了加载block_k瓦片 A 和 B 的延迟。

concurrent_fetch_compute

这种改进的数据移动和计算重叠是通过

添加新的寄存器存储来保存从全局内存预取的数据
将全局到共享内存传输分解为其两个组件，将这两个组件放在内循环（warp 瓦片和 mma 瓦片）的两侧
以及调整外循环中两个__syncthreads()的位置，以实现我们想要的并发性，同时防止竞争条件。

以下是显示数据移动变化前后的伪代码。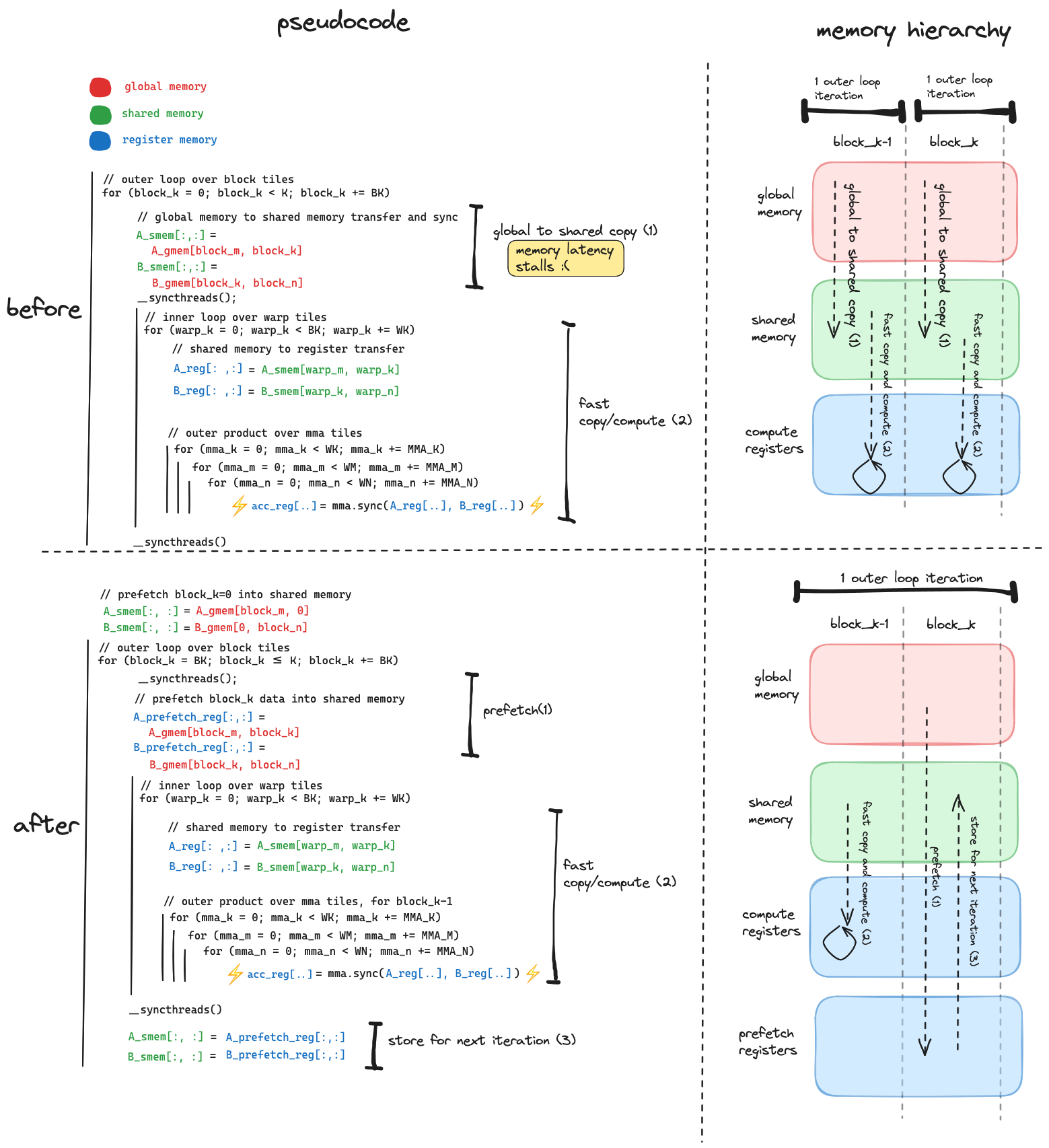 prefetch

这相比之前的核函数带来了显著的加速，使我们达到了约 70%的 HGEMM 核函数性能。

table4

GPU 占用率（插叙）¶

这种优化的潜在成本是需要额外的寄存器存储，每个线程块在寄存器内存中存储两个额外的块瓦片数据。根据 NSight Compute 中的 Launch Statistics 部分，我们从核函数 3 的每个线程使用 104 个寄存器，增加到核函数 4 的每个线程使用 166 个寄存器。这种每个线程资源使用量的增加有可能损害核函数性能，因为它可能影响硬件能够并发执行的线程数量。这是一个关于为什么增加每个线程的寄存器使用可能损害性能的快速插叙，但解释为什么在这种情况下不会。潜在损害核函数性能，因为它可能影响硬件能够并发执行的线程数量。这是一个关于为什么增加每个线程的寄存器使用可能损害性能的快速插叙，但解释为什么在这种情况下不会。

这涉及到一个称为占用率（occupancy）的主题，它是 CUDA 硬件和软件实现的核心。每个流式多处理器（SM）将在芯片上维护尽可能多的线程块的块、warp 和线程执行状态（共享内存、寄存器、程序计数器）。一个 SM 上可以容纳的线程块数量取决于：

每个线程块需要执行多少共享内存、每个线程的寄存器数量以及线程数量（这是给定核函数及其启动配置的属性）
SM 一次可以处理多少共享内存、每个线程的寄存器数量以及线程数量（这是设备的属性，并随着代际更新而改进）

如果给定的核函数实现和启动配置只需要少量寄存器、少量线程和每个块少量共享内存，一个 SM 可以并发执行许多线程块。当多个线程块在 SM 上并发执行时，它们之间的上下文切换是免费的。这使得硬件可以通过跟踪哪些线程能够执行下一条指令、哪些不能，并为准备就绪的线程发出指令，来简单地隐藏停顿和延迟。SM 有越多的线程可供选择，效果越好。这被称为硬件多线程（hardware multithreading），许多关于 CUDA 性能的旧资源将其视为编写快速核函数的主要指导原则。

此时，限制 SM 上可驻留线程块数量的因素是共享内存。每个线程块为 A 矩阵分配一个(256,64)瓦片的共享内存，为 B 矩阵分配一个(64,128)瓦片的共享内存。这总共占用 49KB 的共享内存，而每个 SM 的总共享内存为 62KB，这限制了 SM 上可同时驻留的线程块数量为一个。因此，在这种情况下，由于共享内存是限制因素，使用更多每个线程的寄存器并不重要。

高性能 GEMM 核函数通常具有较低的占用率，意味着它们使用更多的共享内存和每个线程的寄存器内存，并且 SM 上同时驻留的线程较少。这主要是因为需要高算术强度；为了在有限内存带宽下保持计算单元忙碌，内存层次结构低层的每个线程计算越多越好。但低占用率的缺点是 GPU 通过上下文切换自动隐藏延迟的效果会降低。我们可以通过构建核函数以允许计算和数据移动重叠来处理这种权衡，本章就是一个例子。

两个最新的 NVIDIA 架构，Ampere 尤其是 Hopper，引入了专用硬件支持，使我们能够异步执行 GEMM 核函数的多个组件（更多内容见[结论](#经验教训更新的 gpu 更好)）。这种硬件支持使得编写高效、低占用率的核函数（如这些）变得容易得多。

内核 5 - 调整瓦片尺寸¶

在此之前，我发现查看 NSight Compute 中的性能分析结果大约 10 分钟后，就能准确知道核函数中的瓶颈在哪里以及是什么导致的。在核函数 4 达到约 70%的 cuBLAS 吞吐量后，性能分析器通常不会指向单一的性能问题。事后看来，这是因为核函数 4 和 cuBLAS 之间剩余的 30%是许多较小低效之处的产物，而不是单一的一个，性能优化开始更多地基于直觉进行试错，其中一些直觉被证明是错误的。本章描述了两个优化，当一起实施时产生了不错的加速。

调整瓦片尺寸¶

此时我开始思考，如果我的核函数仍然受内存限制，我该如何知道？如果你使用单精度 FFMA 指令，NSight Compute 中的“Speed of Light”部分会显示一个屋顶线图，但如果你使用张量核心则不会。我受到这篇论文的启发，尝试以一种粗略的方式自己弄清楚。

一个更可操作的表述“我是否受内存限制？”问题的方式是“我的核函数的算术强度是否超过机器的平衡点？”

FLOPs performedbytes moved>?τβ

因此，对于左侧，我们需要代入特定于我们核函数的数字，对于右侧，我们需要代入特定于我们硬件的数字。这个部分讨论了算术强度如何是瓦片尺寸的函数。具体来说，对于瓦片尺寸 BM、BN 和 BK，我们应预期的算术强度是 BM∗BNBM+BN。这里是针对块瓦片级别的复习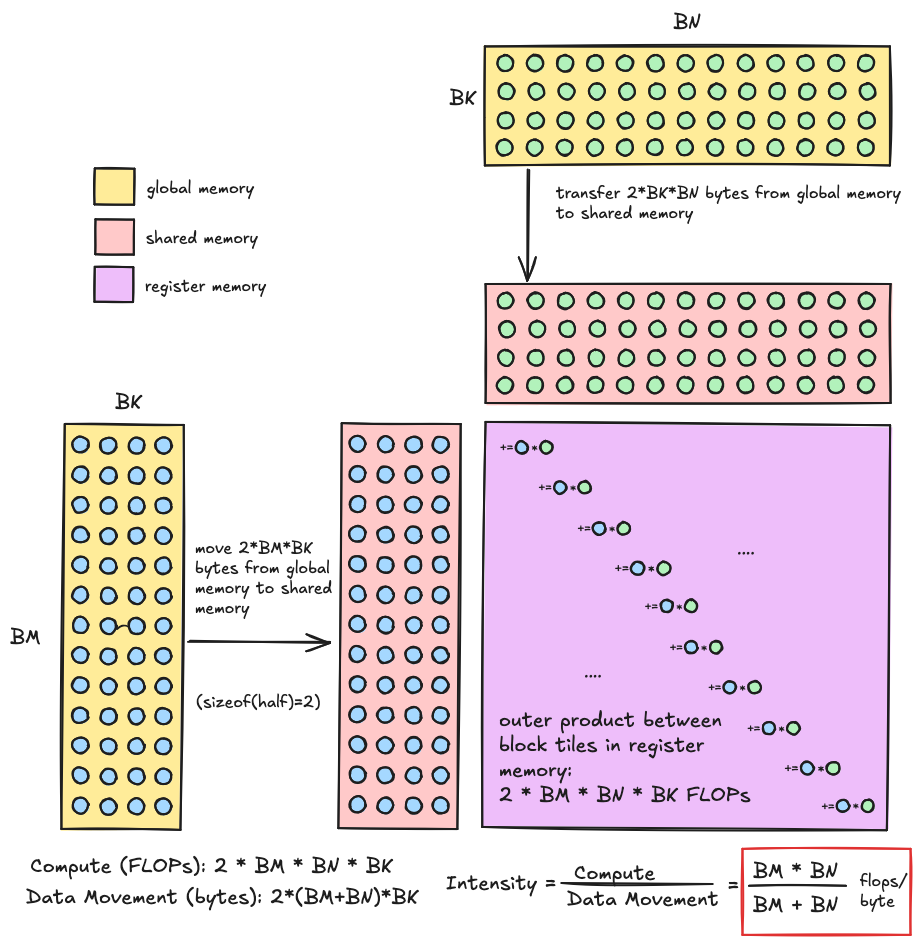 intensity_block_tile_dims 注意 BK 在这个计算中如何被抵消。这意味着在考虑算术强度时，我们沿 K 维度的瓦片大小是无关的。然而，在考虑性能的其他方面时，它并非无关（稍后详述）。

M 和 N 维度 / L2 缓存局部性¶

我们现在需要为我们的机器平衡代入数值。之前在屋顶线图表中，我们将 τHMMA 设置为 cuBLAS hgemm 内核的吞吐量，这可能偏向于低估。在这种情况下，目标是选择足够大的分块维度，使我们舒适地处于屋顶线图的计算受限区域，因此我倾向于在机器平衡的分子中高估算术吞吐量，并在分母中低估内存带宽。

一个合理的高估 τHMMA 是 65,000 GFLOP/秒，这是 T4 数据手册上的理论峰值。

对于分母中的内存带宽，我们希望保守地估计我们实现的内存带宽。为了做到这一点，我们需要考虑 L2 缓存的影响。L2 缓存在 T4 上的 40 个流多处理器之间共享。实际上，这意味着当一个线程块从 DRAM 访问数据时，数据会被移动到 L2 缓存中，其他线程块对相同数据的访问将命中 L2 缓存，直到该数据被逐出。

根据互联网上的人们的说法，线程块按其扁平化块索引的递增顺序执行。官方 CUDA 编程指南指出，不同的线程块独立执行，程序员不应假设不同线程块之间存在任何关系。因此，依赖这个假设来保证正确性可能不明智，但对于 L2 缓存局部性的快速近似计算来说，它是有帮助的。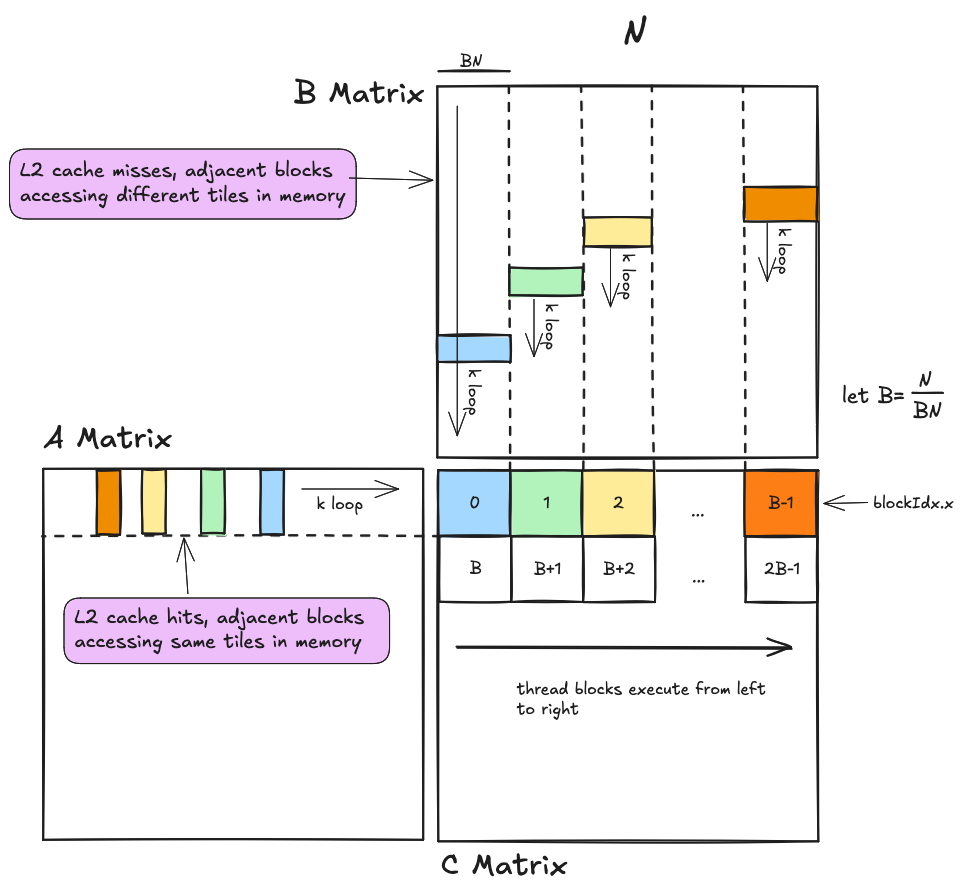 l2_cache_locality 这里的基本思想是，同时执行的线程块对 A 矩阵的访问比对 B 矩阵的访问具有更好的局部性。大多数对 A 的访问应该命中 L2 缓存，而大多数对 B 的访问应该未命中，这意味着我们对于全局内存访问应该实现大约 50% 的命中率。这意味着我们的实现内存带宽是 DRAM 带宽和 L2 缓存带宽的 50/50 加权和。将这个加权和代入机器平衡表达式的分母，最终得到：

BM∗BNBM+BN>?τHMMA0.5∗βDRAM+0.5∗βL2

代入当前块分块维度（BM=256 和 BN=128）、内存带宽和理论算术吞吐量，得到

256∗128 FLOPs256+128 bytes>?65,000∗109 FLOPs/sec0.5∗220∗109+0.5∗1280∗109 bytes/sec

这算出的算术强度为 85.3 FLOPs/byte，机器平衡为 87.24 FLOPs/byte。这两个数字非常接近，表明全局内存访问可能仍然主导我们的总运行时间。如果我们能在共享内存中腾出空间，将 BN 维度从 128 增加到 256 可能值得考虑。如果 BM 和 BN 都是 256，我们估计的算术强度变为 128.0 FLOPs/byte，这应该有望使我们舒适地处于计算受限区域。

当考虑层次结构中的下一级时，高共享内存带宽给了我们更多的调整空间。我们的交错共享内存布局应该实现无存储体冲突的访问，提供 3662 GB/秒的全带宽。warp 分块的 WM 和 WN 维度都是 64。代入数值到这里：

WM∗WNWM+WN>?τHMMAβshmem

得到算术强度为 32 FLOP/byte，平衡点为 17.7 FLOP/byte。因此，可以安全地假设共享内存加载不是我们内核运行时间的主导因素。然而，为了偏向更高的算术强度，我还增加了 WM 和 WN，同时减小了 WK。

K 维度¶

在考虑沿 K 维度的分块大小时，不同的因素开始起作用。在我们的纸笔分析中，沿 K 维度的分块大小在算术强度表达式中被抵消。当思考沿此维度的分块长度时，不同的考虑因素出现。首先，我们可以用它来调整分块的总大小而不影响算术强度。对于块分块，它们消耗的共享内存总字节数为 BK∗(BM+BN)∗sizeof(half)，因此将 BK 增加一个单位会使块分块的总大小增加 (BM+BN)∗sizeof(half)。在决定块分块沿 K 维度的长度时，这成为主要考虑因素。当 BN=256, BM=256 时，我们选择 BK=32，使用这些维度，A 和 B 分块使用的共享内存总量为 32KiB，这正好是每个流多处理器共享内存的一半。这个决定在下一节中是有意义的，该节讨论了一种称为共享内存双缓冲的技术。这种优化涉及为每个输入矩阵在共享内存中分配两个缓冲区，以便一个在写入时另一个可以被读取。当实现双缓冲时，使用这些分块维度，我们将使用设备上可用的每一个字节的共享内存。

分块维度 - 更长更薄¶

这是调整前后的可视化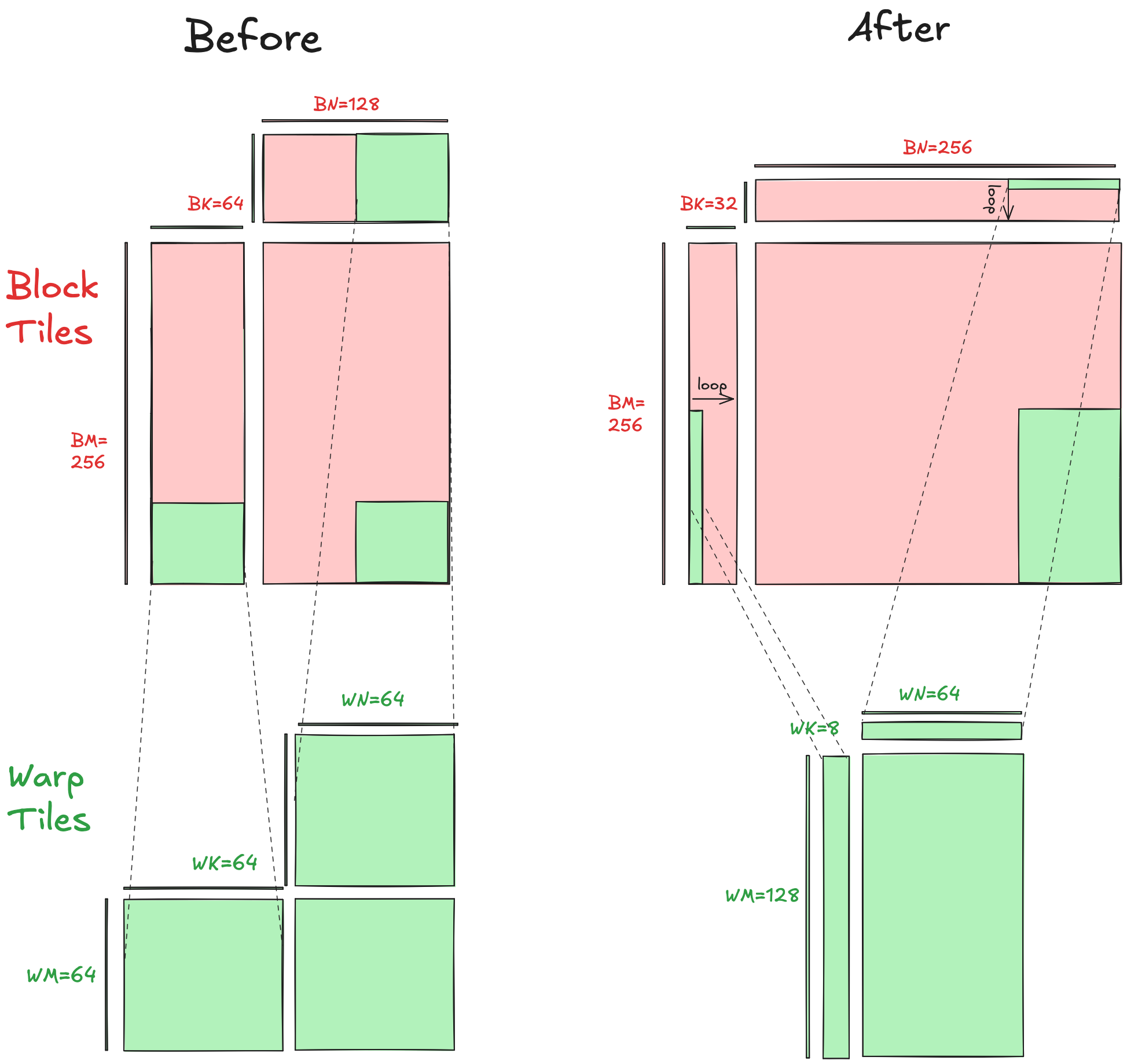：块分块和 warp 分块都变得更长，沿 K 维度更窄，以增加算术强度。为了节省时间，我将此优化与下面讨论的优化结合，因此没有单独测量此优化的性能改进。

优化索引计算¶

此时，我的性能大约是 cuBLAS 的 70%，我使用 NSight Compute 的主要策略是比较我的内核和 cuBLAS HGEMM 内核之间的内核指标。虽然 NVIDIA 没有发布 cuBLAS HGEMM 实现的源代码，但查看 NSight Compute 收集的指标可以让我们深入了解 NVIDIA 的聪明人在编写它时可能使用的优化技术类型。

让我注意到的一点是，cuBLAS HGEMM 执行的总指令数为 94,175,232，而 Kernel 4 执行了 216,227,840 条指令，是 Kernel 4 的两倍多。虽然 Kernel 4 通过更低的每指令周期比（约 8，而 cuBLAS 约 12）部分弥补了这一点，但这确实值得深入研究。

所以我想知道，为什么我的内核执行了两倍的指令数？在 NSight Compute 中展开指令混合部分可以给我们更多信息。 instruction_mix_comparison 答案是 Kernel 4 执行的索引计算相关指令比 cuBLAS 内核多得多。LOP、IADD3 和 SHF 指令是整数和逻辑指令，它们与 tensor core 使用不同的流水线，可以与芯片上其他地方执行的浮点数学运算并发执行。然而，流式多处理器上的每个 warp 调度器每个周期只能发出一条指令，因此大量的索引计算指令可能会挤占 HMMA 指令的发出，而 HMMA 指令是执行繁重工作的 tensor core 指令。那么这些整数和逻辑指令在做什么，为什么会有这么多呢？

根据 NSight Compute，Kernel 4 执行的总指令的 92% 位于循环嵌套中，在这里每个 warp 从共享内存加载其数据区域到寄存器内存，然后通过一系列 HMMA 指令对存储在寄存器内存中的局部矩阵执行外积。将 HMMA 指令映射到其位置的三个嵌套循环都完全展开了，因此那里不需要任何运行时索引计算。

然而，HMMA 指令在存储于寄存器中的 8×8 块上操作，在计算阶段之前，每个 warp 中的线程协作地使用 ldmatrix PTX 指令将所有这些块从交错的共享内存加载到寄存器内存中（参见此处了解 ldmatrix 的解释）。由于此时我们处于块层次结构的最底层，块非常小，因此我们要执行这种索引计算很多次（O(N38)），它涉及乘以一堆步长、计算相对于线程索引的模、以及多个逻辑操作来应用交错函数，所有这些都在运行时发生。

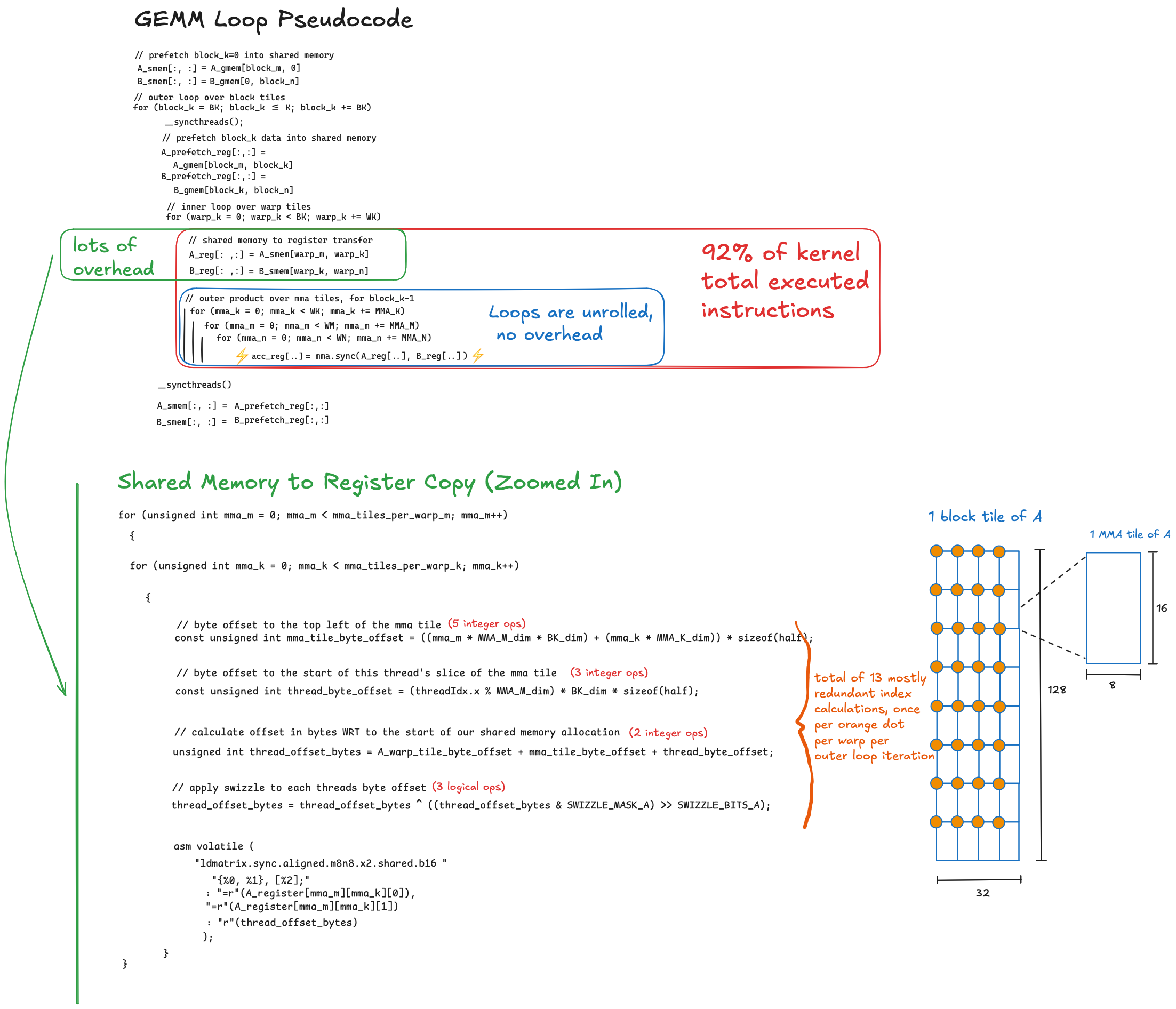
index_calculation_inneficient

为了提高性能，我们应该将尽可能多的计算移到编译时进行，任何需要在运行时发生的计算都应该尽可能精简。在上面显示的索引计算代码中，从根本上说有三个不同且相互依赖的步骤：

首先，每个 warp 计算 mma 块左上角的内存地址
每个线程计算它要加载的元素的内存地址，相对于步骤(1)
因为我们的共享内存布局是交错的，每个线程对步骤(2)中计算的地址应用交错函数，以获得交错布局中的正确内存地址

这三个步骤对每个 8×8 的 MMA 块都要执行。下面是对此的可视化，下图是一个迷你示例，其中每个 MMA 块是四行一列，每个 warp 块有 2×8 个 MMA 块（使用这样更简单的示例可以让我们尽可能明确所有细节，而魔鬼 :smiling_imp: 就在细节中）。

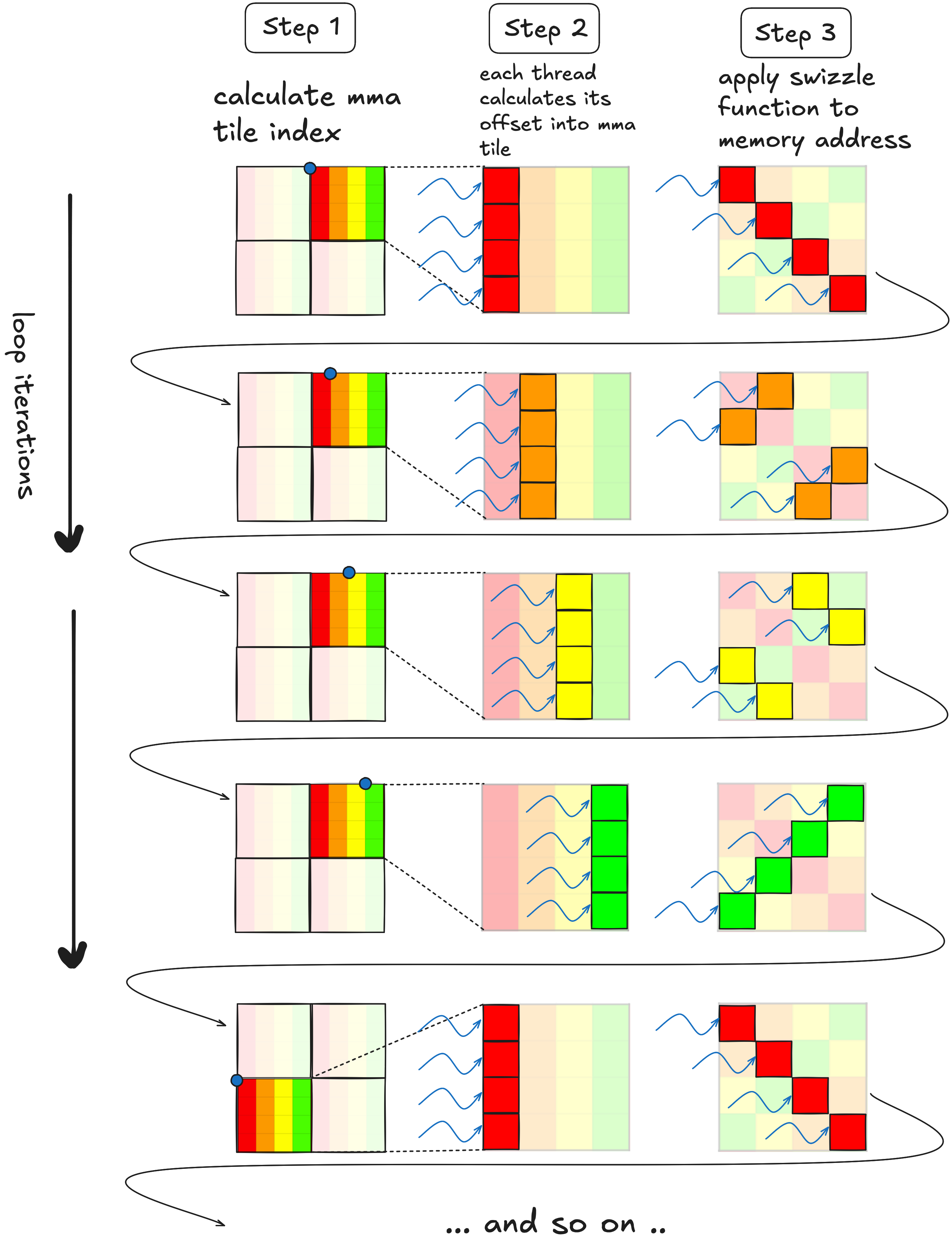
swizzled_index_calculation_inneficient

在中间一列中，每个线程已经计算了它将要加载的值的地址，在未交错的布局中。每次迭代，这些指针向右推进一列，直到到达 warp 块的末尾，此时我们向下移动到下一组行。如果不是交错布局，我们可以在每次迭代中将指针推进一个，即 thread_row+=1。然而，由于数据以交错布局存储，将指针推进到下一组 MMA 块并不仅仅是递增一个的问题。

虽然递增一个无法用于遍历交错布局，但我们可以通过将每个线程的指针与一个常量进行异或来实现等效效果。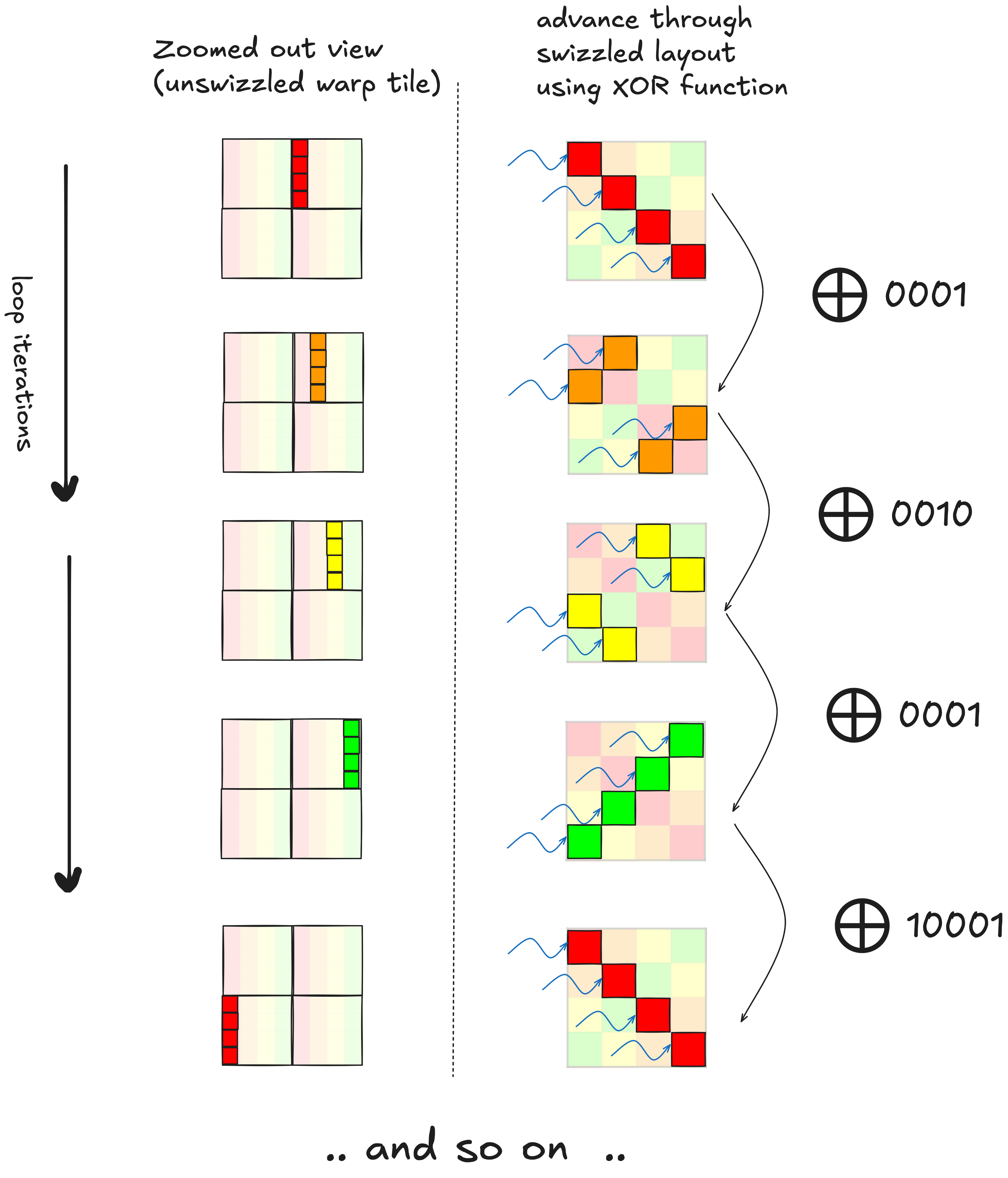 swizzled_index_calculation_efficient 这将每个 ldmatrix 之间的索引计算量从约 13 个操作减少到单个异或操作。应用此优化后，执行的总指令数降至约 90M，略少于 cuBLAS。

这说明了高效遍历交错数据布局的基本原则。在实际代码中，情况要复杂一些，因为交错函数更复杂，而且我们需要遍历 A 和 B 的块，它们彼此的维度不同。此外，包含 ldmatrix 指令的循环是手动展开的，这使得异或操作更容易，也可能让编译器更好地交错 ldmatrix 和 mma.sync 指令，以平衡两个不同流水线之间的负载。

优化的索引计算、循环展开和调整后的块维度都作为同一内核的一部分实现，经过艰苦努力实现了比上一个版本 1.2 倍的加速，使我们达到了 cuBLAS 吞吐量的 86.7%。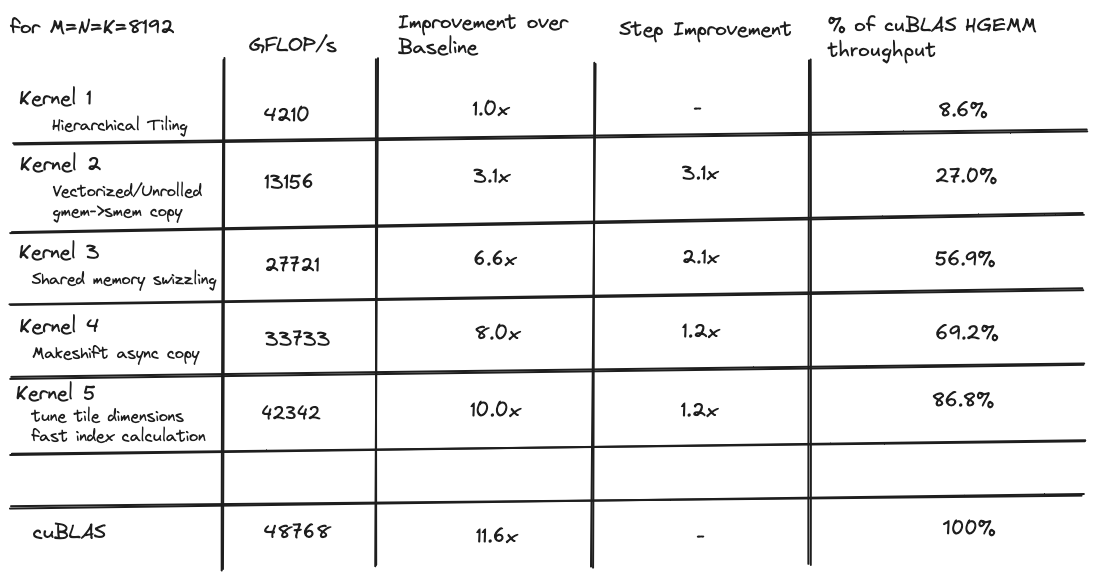 table5

内核 6 - 双缓冲¶

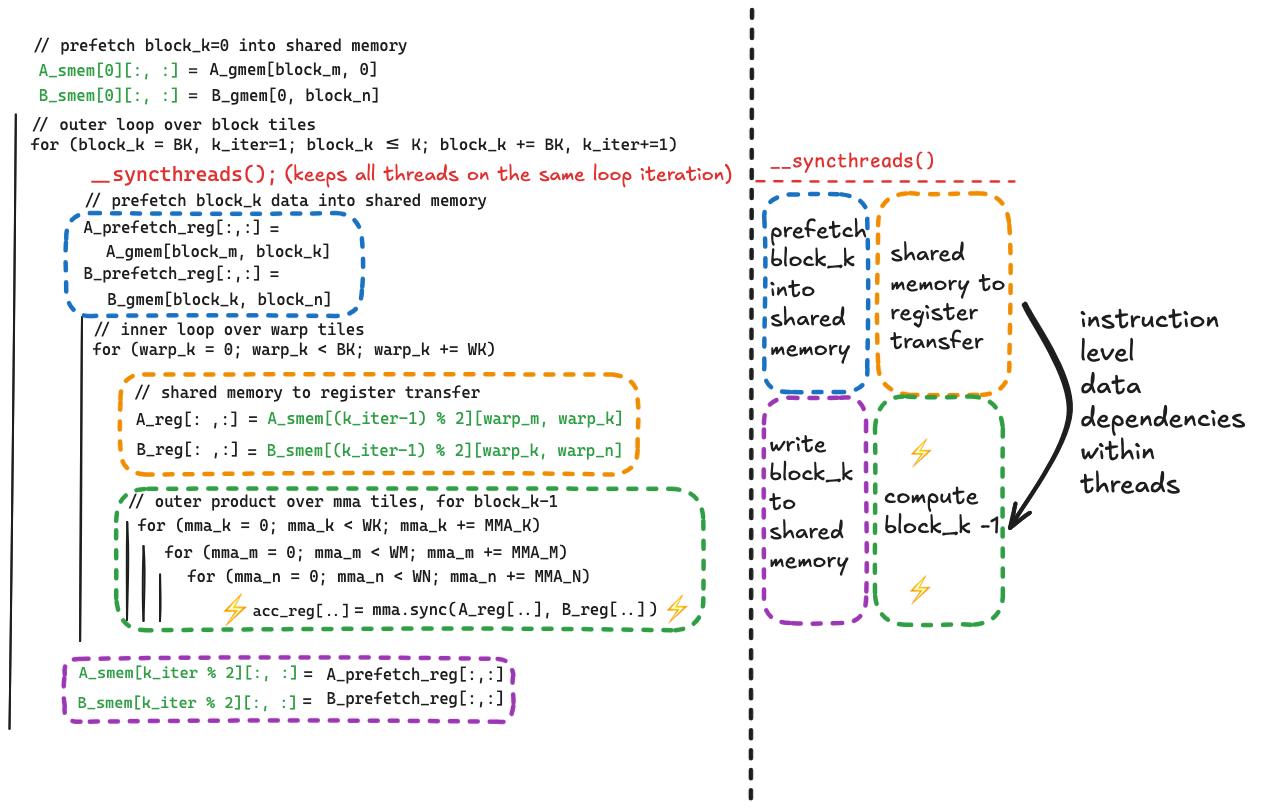
one_syncthreads

这里改变的两件事是移除了其中一个__syncthreads()，以及添加了一个我们始终使用的索引（%2）来跟踪两个缓冲区中哪个正在被读取，哪个在每次迭代中被写入。被读取的缓冲区和被写入的缓冲区在每次迭代中切换。

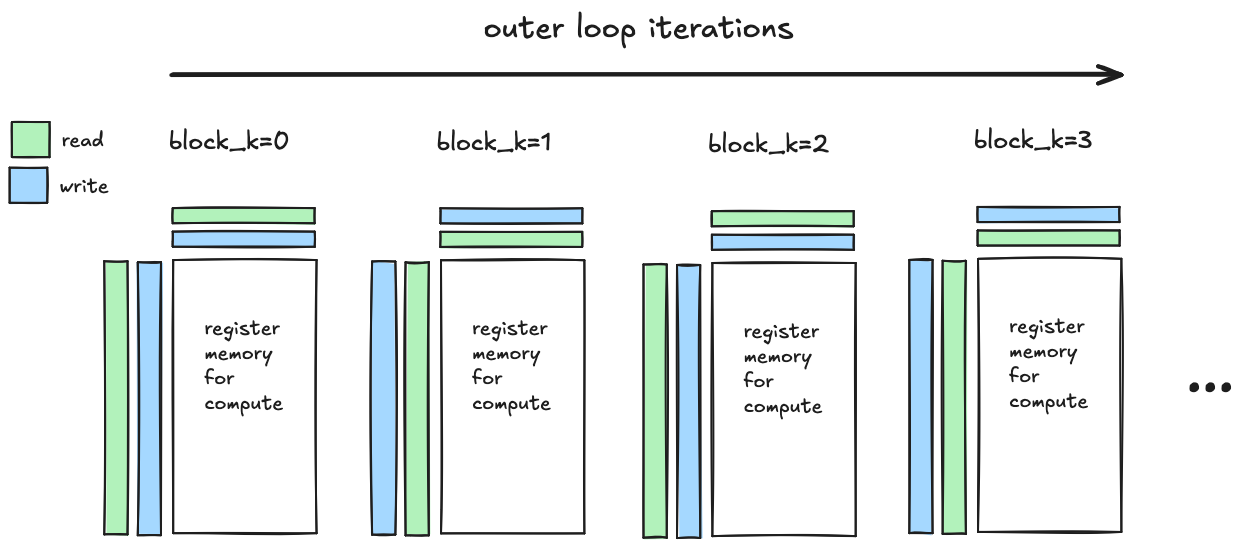
double_buffering

这导致相对于前一个内核有小的加速。但在优化已经高度优化的内核的这个阶段，我会接受我能得到的。

table_6

结论¶

我没有做的事情¶

这就是我结束的地方！有两个进一步性能改进的途径，但我分配的时间用完了。前者比后者容易得多。

优化的尾声- 提醒一下，GEMM 问题是 D=α∗A∗B+β∗C。这是两个计算塞进一个内核中。大部分计算在矩阵乘法 C∗=A∗B 中。一旦我们乘了两个矩阵，然后我们做 D=α∗C∗+β∗C，这通常被称为内核尾声。前者是 O(N³)问题，后者是 O(N²)。当 N 大时，矩阵乘法主导组合算法的运行时间，当 N 较小时尾声更重要。文章完全专注于矩阵乘法，因为这是 GEMM 问题中最有趣和最重要的组成部分。我在所有六个内核中使用的内核尾声是低效的——一旦矩阵乘法完成，结果根据m16n8k8 MMA 布局分散在线程寄存器中，并直接写回内存。这个写入是非合并的，因此达不到理想的带宽和延迟。改进这可能会缩小内核 6 和 cuBLAS 之间对于较小矩阵尺寸的差距。
内循环的手动指令混合调优- 像这个和这个这样的项目使用自定义汇编器匹配/超过 cuBLAS 的性能，允许他们完全用 SASS 编写内核。GEMM 内核的内循环包括共享内存加载和数学指令。如果太多同一类型的指令分组在一起，硬件管道会过载并导致停滞周期。如果你想像我一样完全用 CUDA 和 PTX 编写内核，那么指令调度是编译器的工作，我能够在没有任何内联汇编的情况下获得>90%的 cuBLAS 性能，这意味着 nvcc 可能在这方面做得相当好。然而，如果有人真的决心编写一个对于一系列矩阵尺寸与 cuBLAS 一样快或更快的内核，这个途径可能是必要的。

不同矩阵尺寸上的性能¶

这是一个图表，显示了我编写的内核与 cuBLAS 相比，对于许多不同矩阵维度的性能。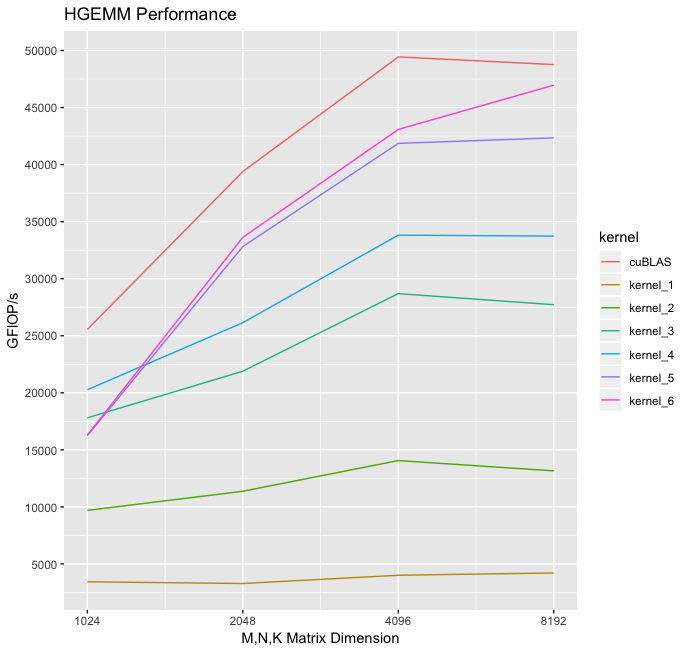 hgemm_performance

注意，我编写的最快内核与 cuBLAS HGEMM 之间的差距对于较小矩阵略大，可能是由于我的未优化尾声。也可能是由于 cuBLAS 选择了专门针对那些矩阵尺寸调优的内核。

经验教训：更新的 GPU 更好¶

考虑到如今有多少人和公司购买 NVIDIA GPU 几乎完全是为了运行矩阵乘法，似乎在连续架构之间，许多工作投入到改进张量核心的可编程性和性能。张量核心吞吐量随着每个新的 SM 架构增加一个数量级，内存带宽也增加，但不成比例。

为了使编程这些强大但不平衡的机器更易于管理，较新的 Ampere 和 Hopper 架构引入了硬件支持，使 GEMM 内核的几个重要部分能够相对于 SM 的其余部分异步运行。Ampere 引入了硬件支持用于异步数据复制从全局内存到共享内存，我使用额外寄存器在内核 4 中实现了一种类似的黑客版本。Hopper 架构引入了一种更高级的功能，称为Tensor Memory Accelerator（张量内存加速器），本质上是一个复制引擎，可以执行索引计算，并相对于 SM 的其他部分异步启动全局内存传输。因此，为 Hopper 编写内核的开发人员可能不必担心索引计算的效率（就像我在内核 5 中所做的那样），因为这部分被卸载到 TMA 的专用硬件中。Hopper 还具有异步张量核心指令，可以从共享内存而非寄存器读写（参见这里）。

所有这些异步性对于低占用率、寄存器密集的 GEMM 内核来说是一件好事。高算术吞吐量意味着我们需要大量快速内存来缓存数据，这意味着每个 SM 无法运行太多线程，这意味着 GPU 不会通过上下文切换自动隐藏我们的延迟，这意味着我们程序员需要更多地思考如何隐藏延迟。这就是异步性有帮助的地方。

所有这些意味着 Hopper 是一种全新且不同的架构，如果你查看 CUTLASS 中针对 Hopper 的 GEMM 内核，代码结构与所有其他sm_90内核不同。Hopper 内核使用生产者/消费者模式，其中相对较少的生产者线程使用 TMA 启动异步数据复制，然后消费者线程管理张量核心。我从未从事过针对 Hopper 的内核工作，所以目前对此了解不多，这篇文章提供了关于为 Hopper 编写内核的用户体验的有趣概述。

这一切都说明，这里讨论的内核针对的是 Turing 架构，该架构在 2018 年是最先进的，如果你正在编写针对 Ampere 或 Hopper 的内核，你用于隐藏延迟的技术将不同且更容易。我使用 Tesla T4 GPU 是因为你可以在 AWS 上以约 50 美分/小时的价格租用它们，这大约是我愿意在 EC2 实例上花费的金额。使用较旧的 GPU 对这个项目来说既是福也是祸，祸在于没有专用硬件支持来隐藏计算索引时的内存延迟，福在于我必须自己完成所有这些工作，这是一次教育经历！

资源 / 致谢¶

大多数这些资源已在本文章的各种地方链接过，但我想将它们全部放在一个地方。这些是一些教育和启发我的资源，没有特定顺序

我从佐治亚理工学院的 Vuduc 教授的高性能计算入门课程中了解了屋顶线模型，所有课程视频都可在这里找到，如果你有时间和兴趣观看，这些视频是极好的免费资源。本文中关于屋顶线和计算强度的部分类似于“局部性基本模型”部分的内容。
这篇文章是这个项目的主要灵感来源。Simon 的其他文章也很出色，这可能是我目前最喜欢的博客之一。
另一篇关于 ML 系统视角的优秀博客。这篇文章特别易读地解释了为什么在 GPU 上训练神经网络时，内存带宽和算术强度等因素很重要。
一篇来自斯坦福大学系统 ML 实验室的文章，关于 Hopper 架构的内核工程。
这是NVIDIA 的 CUTLASS 项目，提供了一系列抽象，使编写快速内核更容易。

Writing Speed-of-Light Flash Attention for 5090 in CUDA C++

12/29/2025

Inside NVIDIA GPUs: Anatomy of high performance matmul kernels

11/2/2025

My first Multi-GPU kernel: Writing All-to-all for AMD MI300X

8/23/2025