Inside NVIDIA GPUs: Anatomy of high performance matmul kernels

发布于 2025-12-29

15580 字

35 min read

标签： CUDA Performance

📝 转载 / 引用来源：作者 www.aleksagordic.com · 查看原文

深入 NVIDIA GPU：高性能矩阵乘法（matmul）内核的剖析¶

从 GPU 架构和 PTX/SASS 到 warp-tiling 和深度异步张量核心（tensor core）流水线

2025 年 9 月 29 日

在这篇文章中，我将逐步介绍支撑最先进（SOTA）NVIDIA GPU 矩阵乘法（matmul）内核的所有核心硬件概念和编程技术。

为什么关注矩阵乘法（matmul）？ Transformer 在训练和推理过程中，大部分浮点运算（FLOPs）都发生在矩阵乘法（matmul）中（如 MLP 中的线性层、注意力 QKV 投影、输出投影等）。这些操作具有极高的并行性，天然适合 GPU。最后，理解矩阵乘法（matmul）内核的工作原理，能为你提供设计几乎所有其他高性能 GPU 内核的工具包。

本文分为四个部分：

NVIDIA GPU 架构基础：全局内存（global memory）、共享内存（shared memory）、L1/L2 缓存，功率限制对 SOL 的影响等。
GPU 汇编语言：SASS 和 PTX
设计接近 SOTA 的同步矩阵乘法（matmul）内核：warp-tiling 方法
在 Hopper 上设计 SOTA 异步矩阵乘法（matmul）内核：利用张量核心（tensor cores）、TMA、计算与加载/存储的重叠、Hilbert 曲线等。

我的目标是让这篇文章自成一体：足够详细以独立存在，又足够简洁以避免成为教科书。

这是更广泛系列的第一部分。在后续文章中，我（理想地）计划涵盖：

在 Blackwell GPU 上设计 SOTA 矩阵乘法（matmul）内核
通过微基准测试实验探索 GPU 架构
设计 SOTA 多 GPU 内核
揭秘内存一致性模型（GPU 中的 tokenizer 等价物：默默支撑系统运行但让大多数开发者困惑的关键组件）

NVIDIA GPU 架构基础¶

要编写高性能 GPU 内核，你需要对硬件有坚实的心理模型。随着我们深入硬件架构，这一点将很快变得清晰。

在本文中，我专注于 Hopper H100 GPU。如果你深入理解 Hopper，将知识适配到未来架构（Blackwell、Rubin）或早期架构（Ampere、Volta）会变得直接。

Hopper [1] 和 Ampere [2] 白皮书是很好的信息来源。

在最高层面，GPU 执行两个基本任务：

移动和存储数据（内存系统）
对数据进行有用工作（计算流水线）

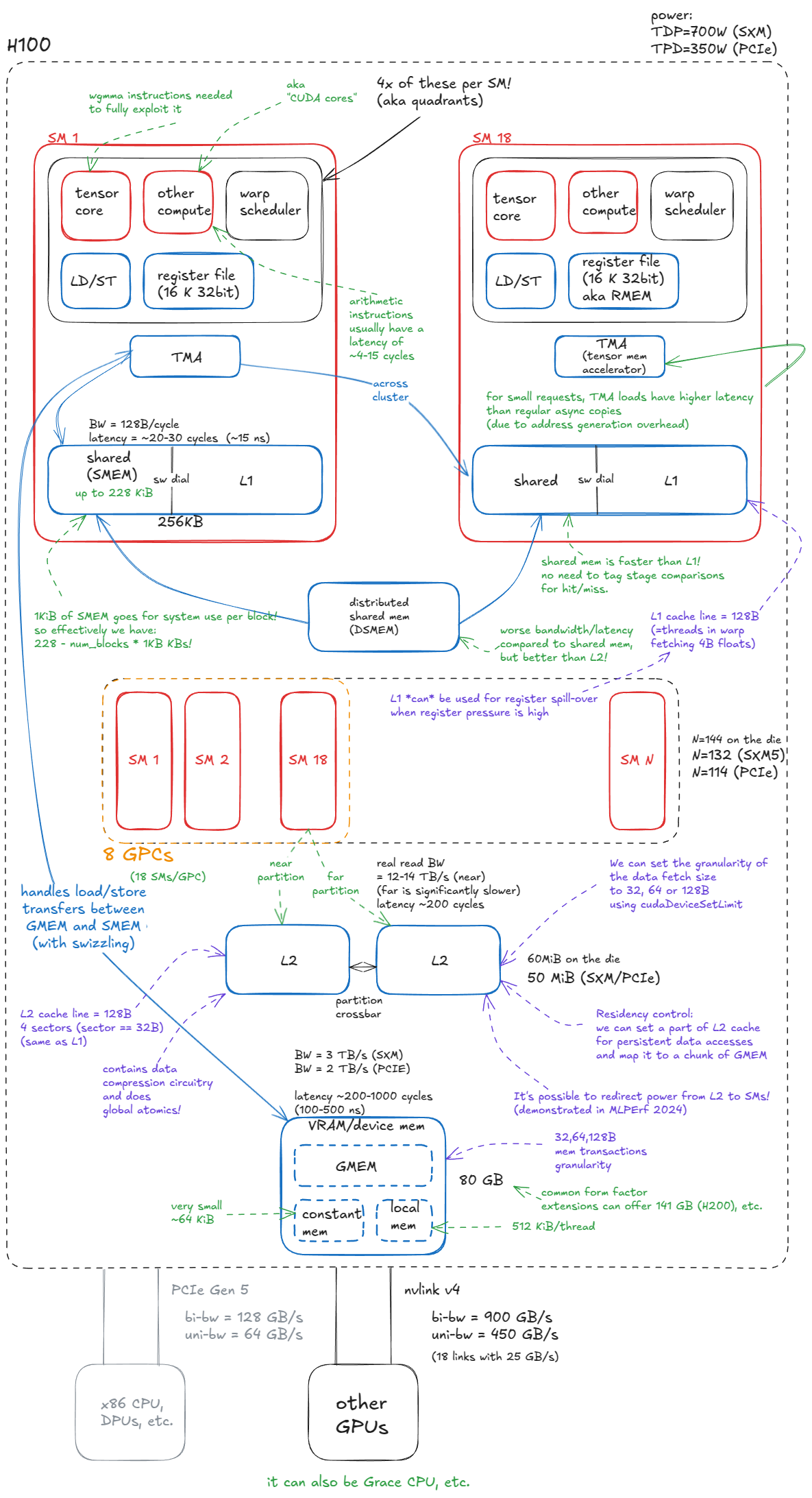
下面的 H100 框图反映了这种划分：蓝色组件代表内存或数据移动，而红色组件是计算（热）单元。

图 1：NVIDIA Hopper H100 GPU 模型

图 1：NVIDIA Hopper H100 GPU 模型

如果你发现文章中有任何错误，请私信我——欢迎在 X 或 LinkedIn 上给我留言，或通过匿名反馈。

内存¶

GPU 中的内存系统是高度分层的，类似于 CPU 架构。

这种层次结构由物理和电路设计决定：SRAM 单元更快但更大（实现其速度的控制电路也增加了面积），而 DRAM 单元更小/密度更高但更慢。结果是快速内存容量较小且昂贵，而较慢的内存可以提供更大的容量。我们将在后面更详细地介绍 DRAM 单元/内存。

这种容量和延迟之间的权衡正是缓存层次结构存在的原因。在理想世界中，每个计算单元旁边都会有一大块超快内存。由于这在物理上不可能，GPU 设计者妥协：将少量快速内存放置在计算单元附近，并由逐渐更大、更慢的内存池支持。这种组织方式最大化整体系统吞吐量。

GPU 内存系统包括：

设备内存（device memory）（VRAM）。在 CUDA 术语中，“设备”内存指片外 DRAM——物理上与 GPU 芯片分离但封装在同一板上——实现为堆叠 HBM。它承载全局内存（GMEM）、每线程“本地”内存（寄存器溢出空间）等。
L2 缓存。一个大型的 k 路组关联 SRAM 缓存。它物理上分为两部分；每个 SM 直接连接到一个分区，并通过交叉开关间接连接到另一个分区。
分布式共享内存（DSMEM）。物理上接近的一组 SM（一个 GPC）的池化共享内存（SMEM）。
L1 缓存和共享内存
1. L1 缓存。一个较小的 k 路组关联 SRAM 缓存，每个 SM 私有。
2. 共享内存（SMEM）。程序员管理的片上内存。SMEM 和 L1 共享相同的物理存储，它们的相对分割可以在软件中配置。
寄存器文件（RMEM）。最快的存储，位于计算单元旁边。寄存器是各个线程私有的。与 CPU 相比，GPU 包含更多寄存器，总 RMEM 容量与 L1/SMEM 存储的总和大小相同。

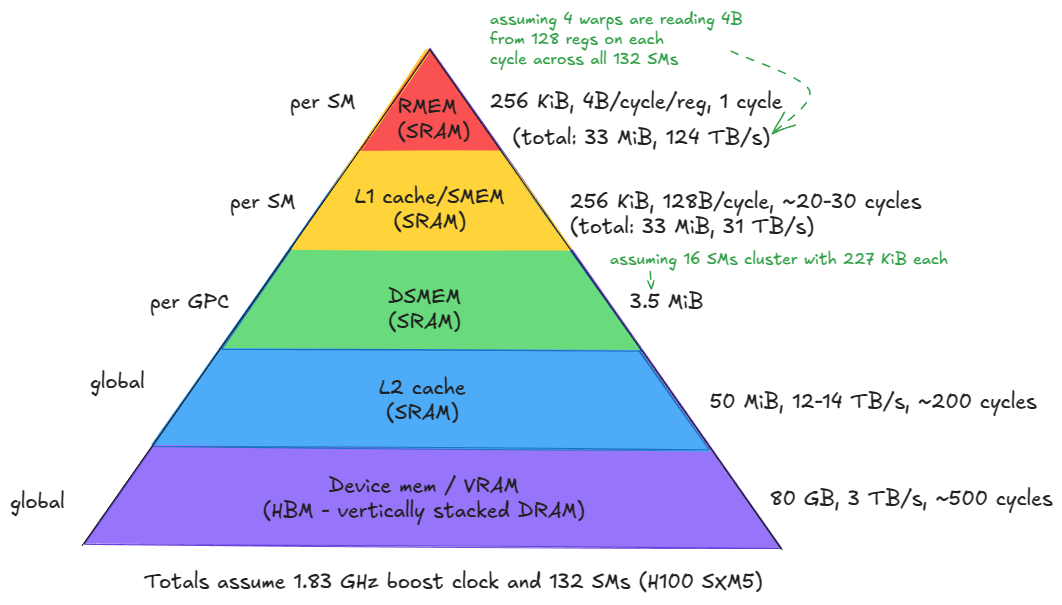
图 2：H100（SXM5）GPU 的内存层次结构

图 2：H100（SXM5）GPU 的内存层次结构

📝注意：

还有其他一些较小的指令缓存，以及常量内存等，我将忽略它们，因为它们对我们的理解不重要。

从设备内存向下到寄存器（级别 1-5），你可以看到一个清晰的趋势：带宽增加几个数量级，而延迟和容量减少类似的数量级。

由此得出几个直接含义：

将最频繁访问的数据尽可能靠近计算单元。
最小化对层次结构较低级别的访问，尤其是设备内存（GMEM）。

另一个值得注意的组件是张量内存加速器（TMA），随 Hopper 引入。TMA 支持全局内存和共享内存之间以及集群内共享内存之间的异步数据传输。它还支持 swizzling 以减少 bank 冲突——我们将适时（双关语）介绍这些细节。

计算¶

从内存转向计算，基本单元是流式多处理器（streaming multiprocessor，SM）。Hopper H100（SXM5）总共集成了 132 个 SM。

SM 被分组为图形处理集群（graphics processing clusters，GPC）：每个 GPC 包含 18 个 SM，GPU 上有 8 个 GPC。四个 GPC 直接连接到一个 L2 分区，另外四个连接到第二个分区。

📝备注：

GPC 也是支撑 CUDA 中线程块集群抽象的硬件单元——我们稍后会回到编程模型。

关于集群的一个要点：之前我说每个 GPC 有 18 个 SM，所以有 8 个 GPC 时，我们预计有 144 个 SM。但 SXM/PCIe 外形规格暴露了 132 或 114 个 SM。差异在哪里？这是因为 18×8 的布局仅适用于完整的 GH100 芯片——在实际产品中，一些 SM 被熔断关闭。这直接影响我们编写内核时如何选择集群配置。例如，你不能使用所有 SM 来跨越超过 2 个 SM 的集群。

最后，请注意图形处理集群（GPC）中的“图形”是一个遗留术语。在现代服务器级 GPU 中，这些集群纯粹用作计算/AI 加速单元，而不是图形引擎。GPU 也是如此，去掉 G，它们就是 AI 加速器。

除了已经提到的 L1/SMEM/TMA/RMEM 组件（所有这些都物理位于 SM 内），每个 SM 还包含：

张量核心。执行小矩阵块（例如，64x16 @ 16x256）上矩阵乘法的专用单元，具有高吞吐量。大型矩阵乘法被分解为许多这样的块操作，因此有效利用它们对于达到峰值性能至关重要。
CUDA 核心和 SFU。所谓的“CUDA 核心”（营销术语）执行标准浮点运算，如 FMA（融合乘加：c = a * b + c）。特殊功能单元（SFU）处理超越函数，如sin、cos、exp、log，但也处理代数函数，如sqrt、rsqrt等。
加载/存储（LD/ST）单元。服务加载和存储指令的电路，与 TMA 引擎互补。
Warp 调度器。每个 SM 包含调度器，为 32 个线程的组（在 CUDA 中称为 warp）发出指令。一个 warp 调度器每个周期可以发出一个 warp 指令。

每个 SM 在物理上分为四个象限，每个象限容纳上述计算单元的一个子集。

这引出了以下见解：

📝并行性与并发性

一个 SM 最多可以同时发出四个 warp 的指令（即，在给定周期内，真正并行执行 128 个线程）。

然而，一个 SM 可以容纳多达 2048 个并发线程（64 个 warp）。这些 warp 是常驻的，并随时间调度进出，允许硬件隐藏内存/流水线延迟。

换句话说，指令并行性（有多少线程在给定周期开始执行指令）每个 SM 一次限制为 128 个线程（4 个 32 宽的 warp 指令），而并发性（调度器中跟踪并符合运行条件的线程数）扩展到 2048 个线程。

光速与功率节流¶

既然我们购买 NVIDIA GPU 是为了计算，很自然地会问：天花板是什么——GPU 的最大计算吞吐量？这通常被称为“光速”（SoL）性能：由芯片物理特性决定的上限。

根据数据类型有多个天花板。在 LLM 训练工作负载中，bfloat16（bf16）近年来一直是主导格式，尽管fp8和 4 位格式正变得越来越重要（对于推理，fp8 相当标准）。

峰值吞吐量计算为：perf = freq_clk_max * num_tc * flop_per_tc_per_clk

或用文字描述：最大时钟频率 × 张量核心数量 × 每个张量核心每个周期的 FLOPs。

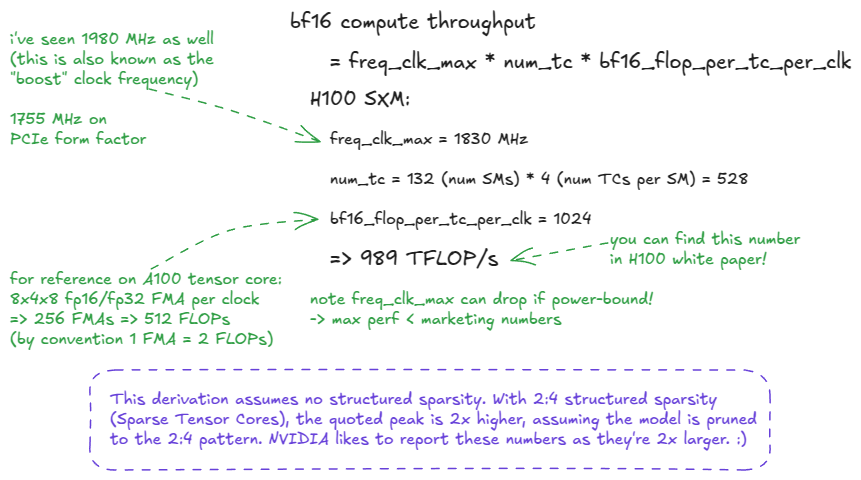
Figure 3: H100 SXM5 BF16 speed-of-light derivation

图 3：H100 SXM5 BF16 光速推导

📝FLOP vs FLOPs vs FLOPS vs FLOP/s

FLOP = 单个浮点运算。
FLOP/s = 吞吐量单位：每秒浮点运算次数。
FLOPs（小写 s）= FLOP 的复数形式（运算）。
FLOPS（全大写）常被误用来表示吞吐量，但严格来说应仅读作“FLOPs”（FLOP 的复数形式）。FLOPS 用作 FLOP/s 是马虎的！ :)

我在上图留下了一个提示：“光速”实际上不是恒定的（我猜这是类比失效的地方）。

实际上，峰值吞吐量取决于实际时钟频率，这可能在功率或热节流下变化。如果 GPU 时钟下降，有效光速也会下降：

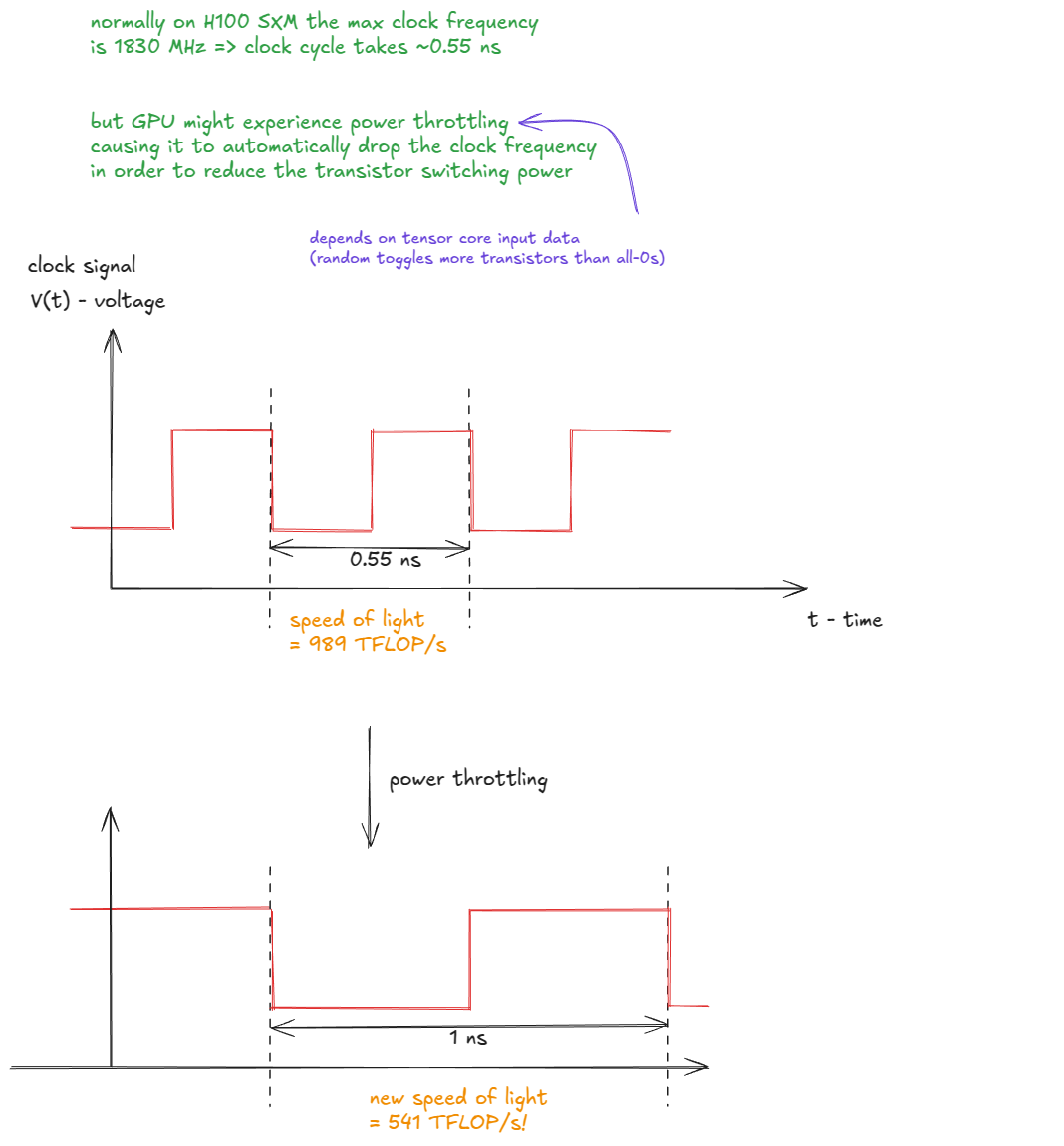
Figure 4: Power throttling reduces clock frequency and lowers the effective “speed of light”

图 4：功率节流降低时钟频率并降低有效“光速”

📝进一步阅读：

Horace He 在他的博客文章 [3] 中更深入地探讨了这一现象。

这就是我们目前需要的硬件细节。

接下来，我们将把重点转向 CUDA 编程模型，然后深入一层硬件，最终上升到 CUDA C++领域。

CUDA 编程模型¶

CUDA 编程模型自然地映射到 GPU 硬件和内存层次结构。

关键抽象是：

线程
warp（32 个线程）
线程块
线程块集群
网格（线程块或集群的）

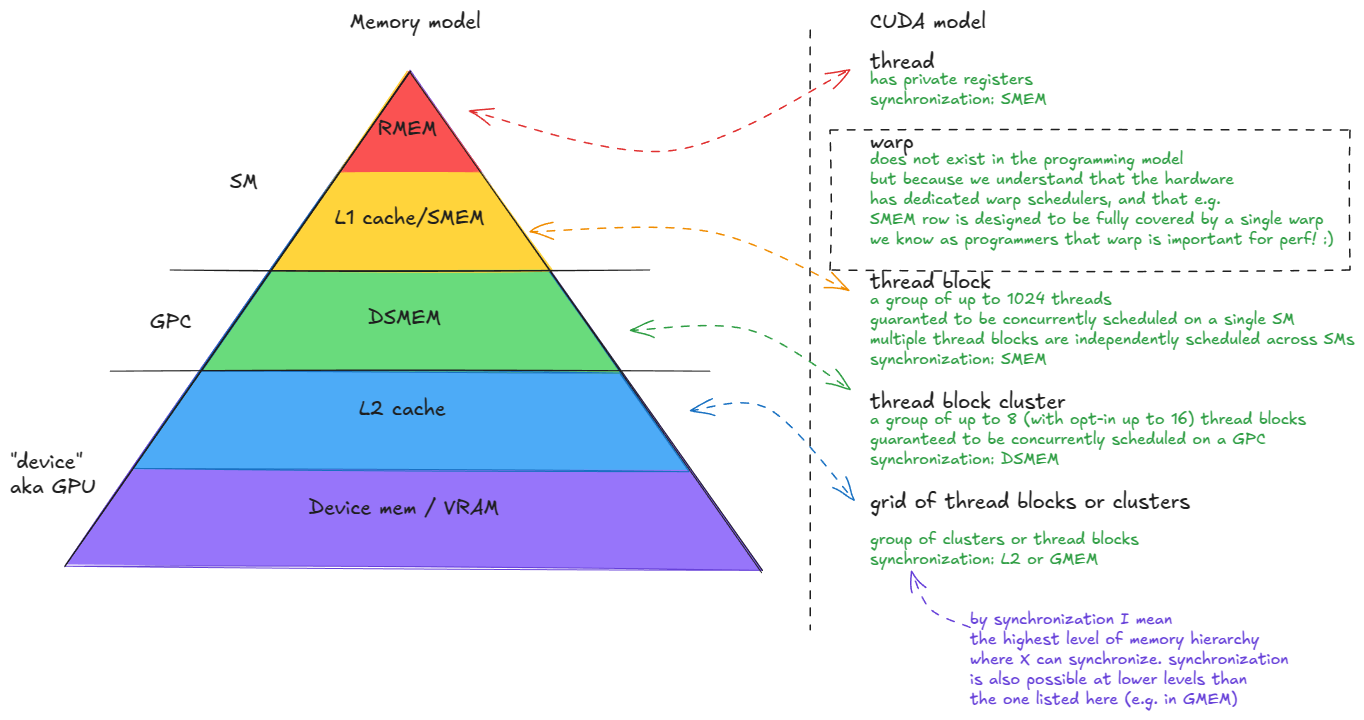
Figure 5: CUDA Programming Model: threads, warps, blocks, clusters, grids

图 5：CUDA 编程模型：线程、warp、块、集群、网格

每个线程通过变量如gridDim、blockIdx、blockDim和threadIdx“感知”其在 CUDA 层次结构中的位置。内部上，这些存储在特殊寄存器中，并在内核启动时由 CUDA 运行时初始化。

这种位置信息使得在 GPU 上分配工作变得容易。例如，假设我们要处理一个 1024×1024 的图像。我们可以将其划分为 32×32 的线程块，每个块包含一个 32×32 的线程排列。

然后每个线程可以计算其全局坐标，例如

const int x = blockIdx.x * blockDim.x + threadIdx.x
const int y = blockIdx.y * blockDim.y + threadIdx.y

const int x = blockIdx.x * blockDim.x + threadIdx.x
const int y = blockIdx.y * blockDim.y + threadIdx.y

，并使用这些坐标从全局内存（image[x][y]）中获取其分配的像素，执行一些逐点操作，并将结果存储回去。

以下是这些变量之间的关系：

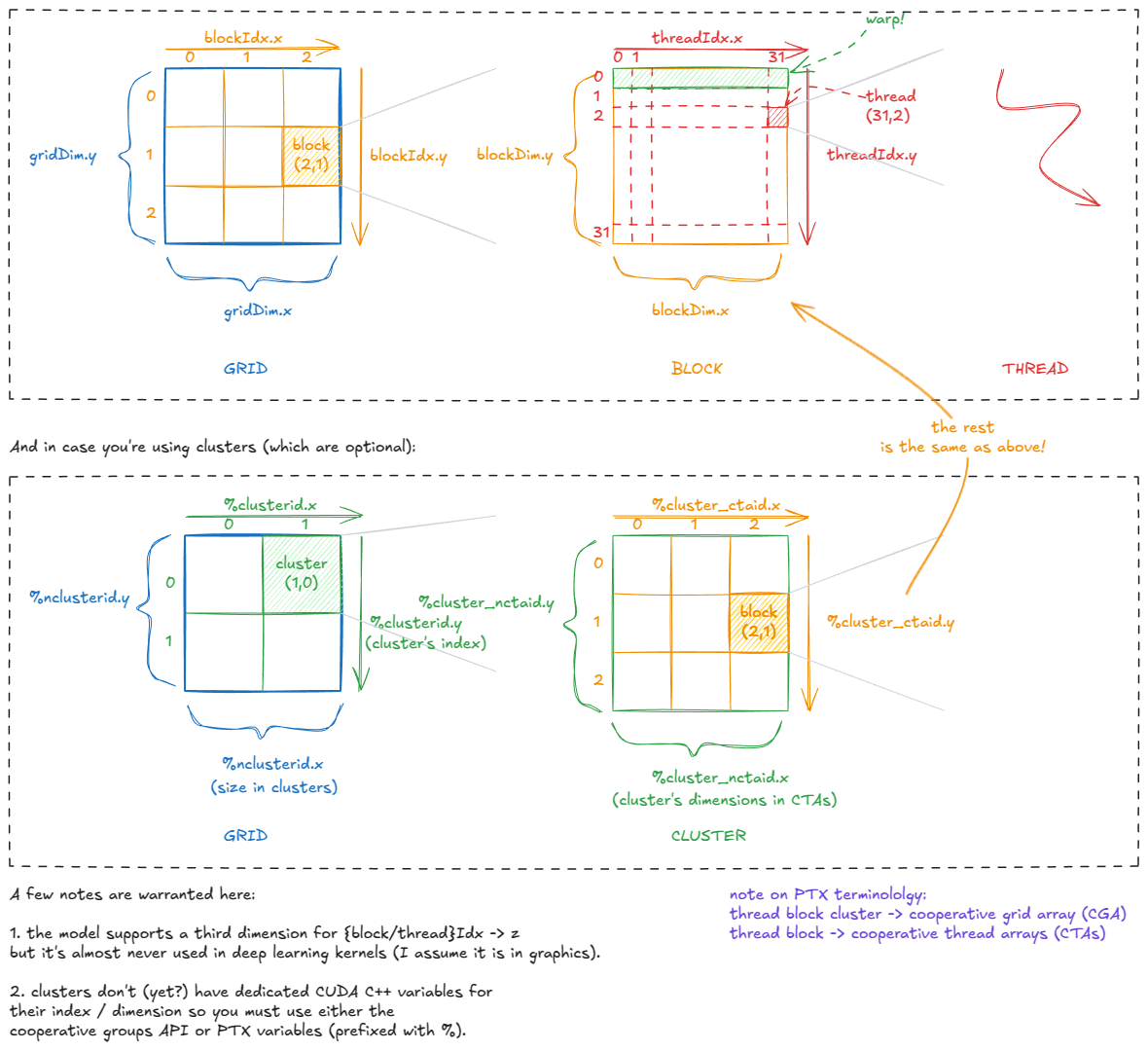
图 6：CUDA 内置变量：线程如何知道自身位置

图 6：CUDA 内置变量：线程如何知道自身位置

如图所示，在实践中我们主要使用一维或二维的网格/集群/块形状。不过，在内部，它们总是可以根据需要逻辑重组。

例如，如果threadIdx.x从 0 到 1023 运行（一个包含 1024 个线程的一维块），我们可以将其拆分为x = threadIdx.x % 32和y = threadIdx.x / 32，从而有效地将块重塑为 32×32 的逻辑二维布局。

将 CUDA 模型与硬件联系起来，现在应该清楚一个事实：一个线程块应至少包含 4 个 warp（即 128 个线程）。

为什么？

一个线程块驻留在单个 SM 上。
每个 SM 有 4 个 warp 调度器——因此，为了充分利用硬件，您不希望它们闲置。

📝更多关于 4 个 warp 的原因：

我们稍后将深入探讨，但请注意，在 Hopper 架构上，warp 组（4 个 warp）是 WGMMA（矩阵乘法）张量核心指令的执行单元。

此外，对于持久内核（persistent kernels），我们通常每个 SM 只启动一个线程块，因此重要的是结构化工作，以保持所有 warp 调度器忙碌。

掌握了 CUDA 编程模型的术语后，我们现在可以继续深入 GPU 架构。

GMEM 模型¶

让我们深入 GMEM。如前所述，它实现为 DRAM 层的堆栈，底部是逻辑层（HBM）。但 DRAM 到底是什么？

图 7：DRAM 单元内部：晶体管+电容器，字线+位线

图 7：DRAM 单元内部：晶体管+电容器，字线+位线

现在我们已经理解了单个位是如何存储的，让我们放大到整个内存矩阵。从高层次看，它看起来像这样：

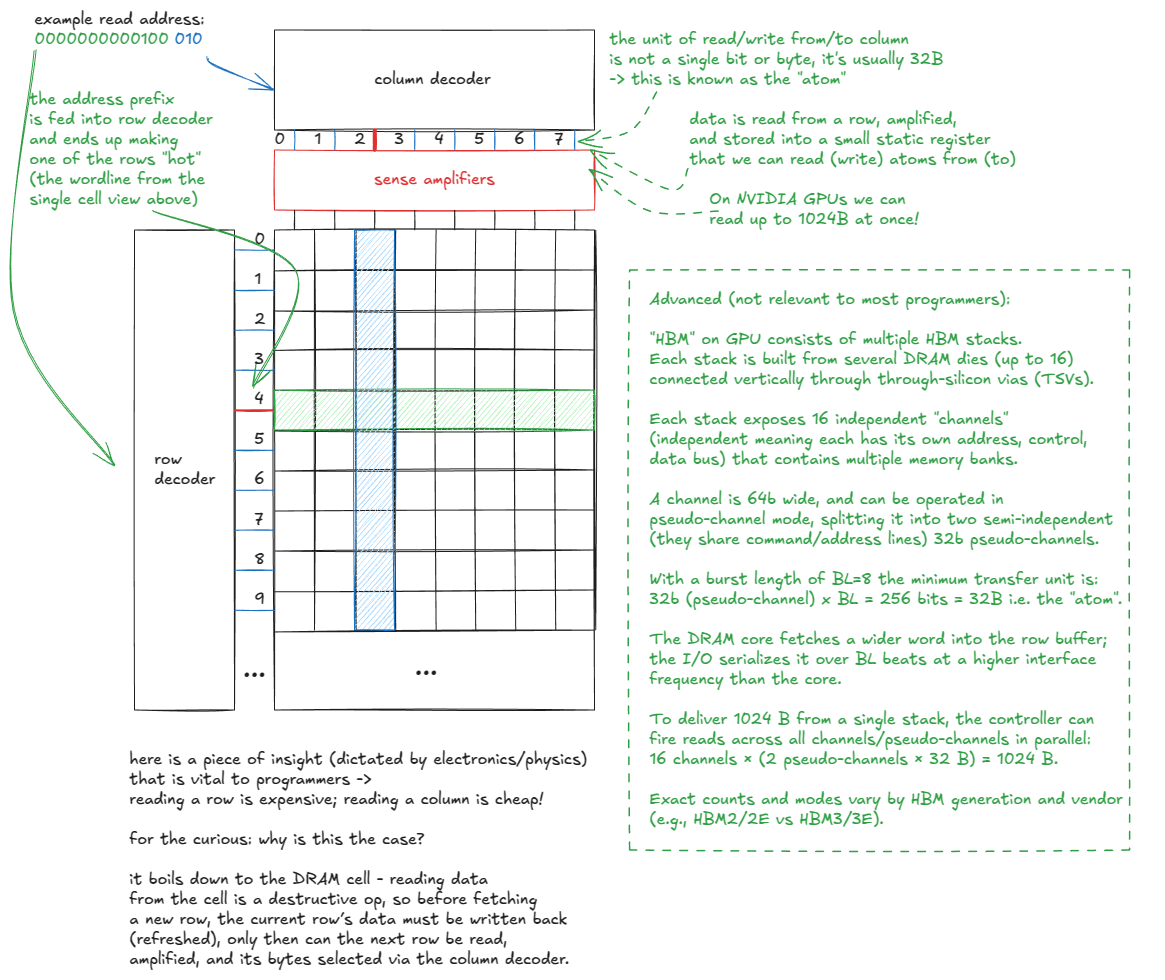
图 8：GMEM 模型

图 8：GMEM 模型

📝关于 HBM 的进一步阅读：

如果您想更深入了解 HBM，我发现论文 “揭秘高带宽内存（High Bandwidth Memory）在实时系统中的特性” [21] 相当有启发性。

因此我们得出结论：由于 DRAM 单元的物理特性，访问模式很重要。这里有一个例子：

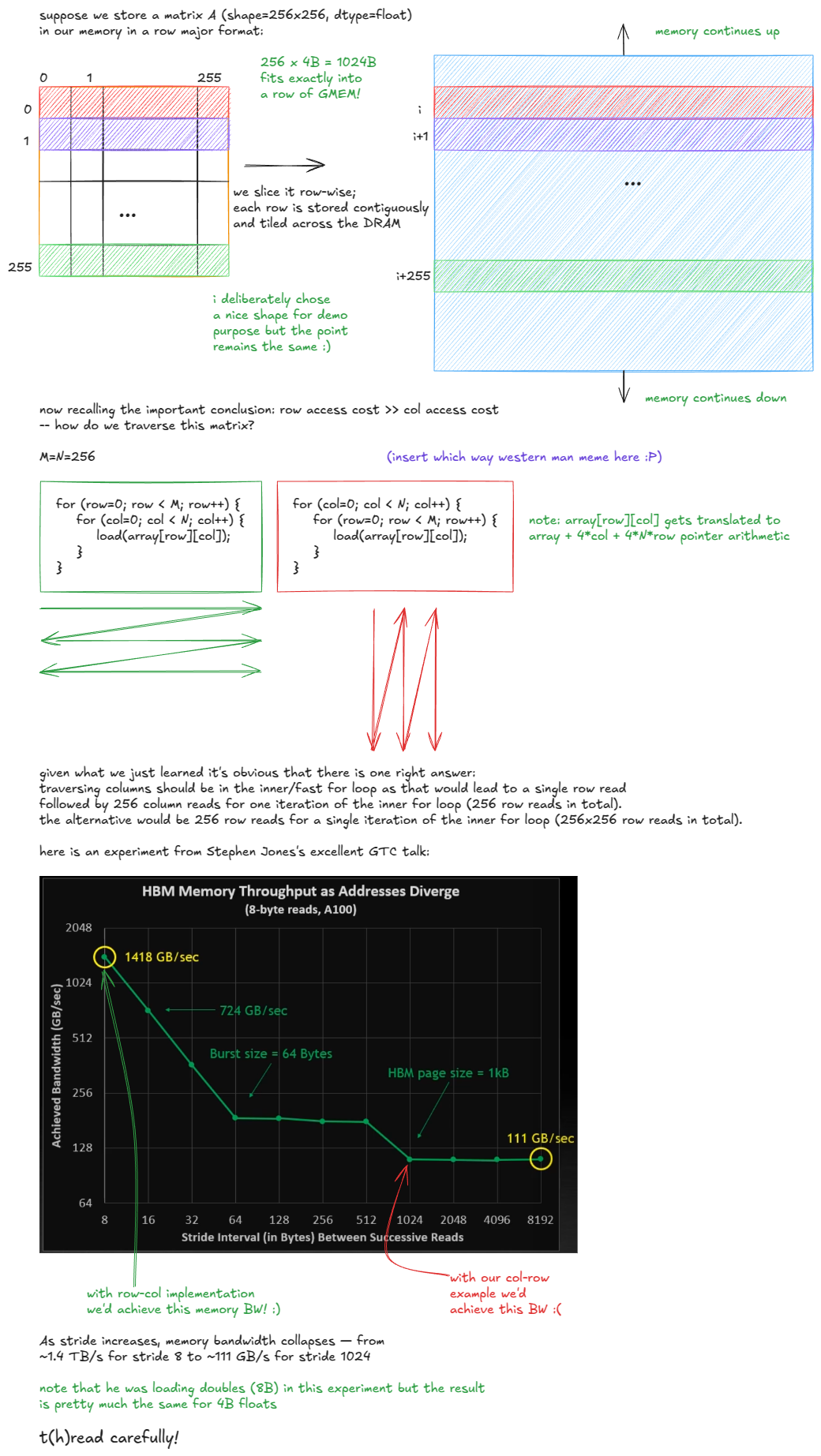
图 9：GMEM 中访问模式的影响

图 9：GMEM 中访问模式的影响

Stephen Jones 的演讲 “CUDA 编程如何工作” [4] 值得一看。

如果我们的示例中的矩阵是列优先的，情况会反转：列中的元素将连续存储，因此高效的选择是在内循环中遍历行以避免 DRAM 惩罚。

所以当人们说“GMEM 合并（coalescing）非常重要”时，他们的意思是：线程应访问连续的内存位置，以最小化触及的 DRAM 行数。

接下来，让我们关注 SMEM 的工作原理。

SMEM 模型¶

共享内存（SMEM）具有非常不同于 GMEM 的特性。它由 SRAM 单元而非 DRAM 构建，这赋予了它根本不同的速度和容量权衡。

SRAM 单元的确切设计并不重要——只需知道存储单个位信息需要更多晶体管。您可以随时搜索“SRAM 单元”。

SMEM 组织为 32 个 bank，每个 bank 宽 32 位（4 字节）：

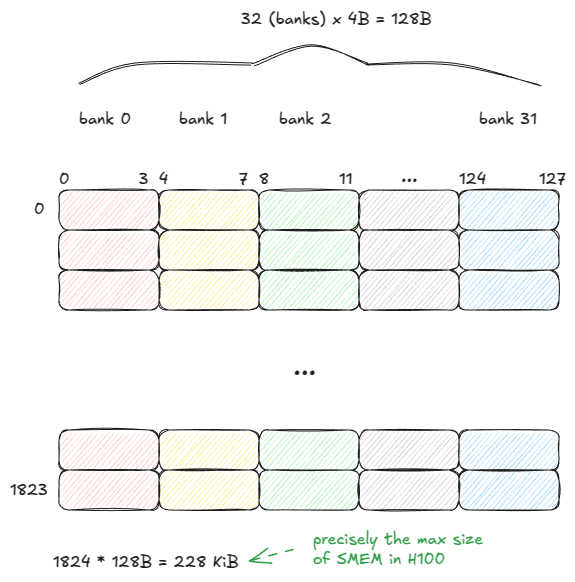
图 10：SMEM 模型

图 10：SMEM 模型

SMEM 可以在单个周期内从所有 32 个 bank（128B）提供数据——但前提是遵守一条规则：

一个 warp 中的线程不得访问同一 bank 内的不同地址。否则，这些请求将在多个周期内串行化。

这种情况被称为bank 冲突（bank conflict）。如果 N 个线程访问同一 bank 的不同地址，结果是 N 路 bank 冲突，warp 的内存请求需要 N 个周期完成。

在最坏情况下，所有 32 个线程针对同一 bank 的不同地址，吞吐量下降 32 倍。

为了说明，假设 warp 大小为 5。以下两种访问模式将分别需要 3 个周期和 1 个周期来服务：

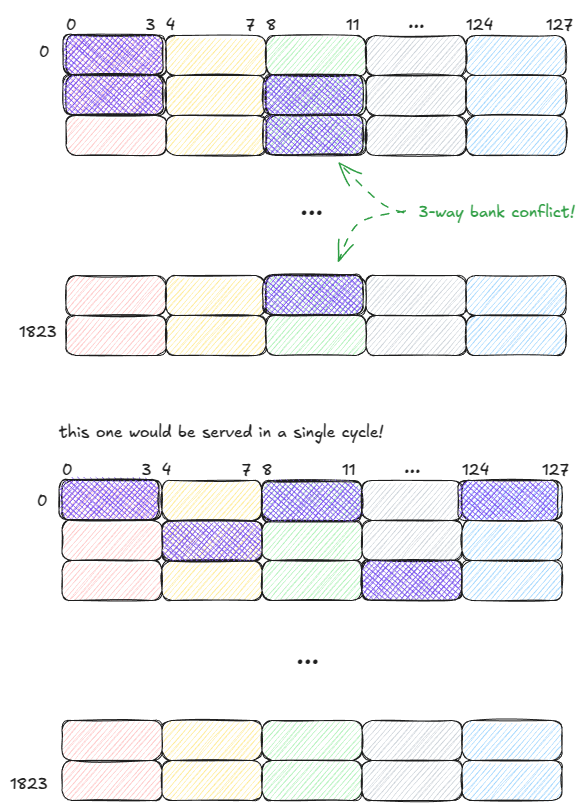
图 11：SMEM：良好与不良访问模式

图 11：SMEM：良好与不良访问模式

重要的是：如果 warp 中的多个线程访问同一 bank 内的相同地址，SMEM 可以广播（或多播）该值给所有线程。

在下面的示例中，请求在单个周期内服务：

Bank 1 可以向 2 个线程多播一个值。
Bank 2 可以向 3 个线程多播一个值。

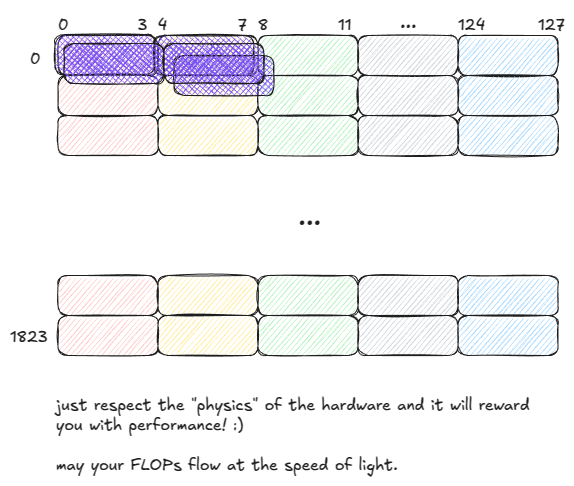
图 12：SMEM：多播（在单个周期内服务）

图 12：SMEM：多播（在单个周期内服务）

现在，对于硬件拼图的最后一块：L1 缓存。

这是 Axel 关于 SMEM 微基准测试的一篇优秀博客文章 [5]。

L1 模型¶

我们已经看到 L1 和 SMEM 共享相同的物理存储，但 L1 在该存储周围添加了一个硬件管理的脚手架层。

从高层次看，L1 缓存的逻辑流程是：

一个 warp 发出内存请求（到 SMEM 或 GMEM）。
请求进入 MIO 管道并分发到 LSUIN 路由器。
路由器引导请求：SMEM 访问立即从数据数组服务，而 GMEM 访问进入标签比较阶段。
在标签阶段，GMEM 地址标签与目标集合中存储的标签比较，以确定数据是否驻留在 L1 中。
在命中（hit）时，请求直接从数据数组服务（就像 SMEM 一样）。
在未命中（miss）时，请求传播到 L2（如果需要，进一步到 GMEM 或对等 GPU 内存）。当数据返回时，它被缓存在 L1 中，驱逐现有行，并并行发送回请求 warp。

这是我刚刚描述的系统：

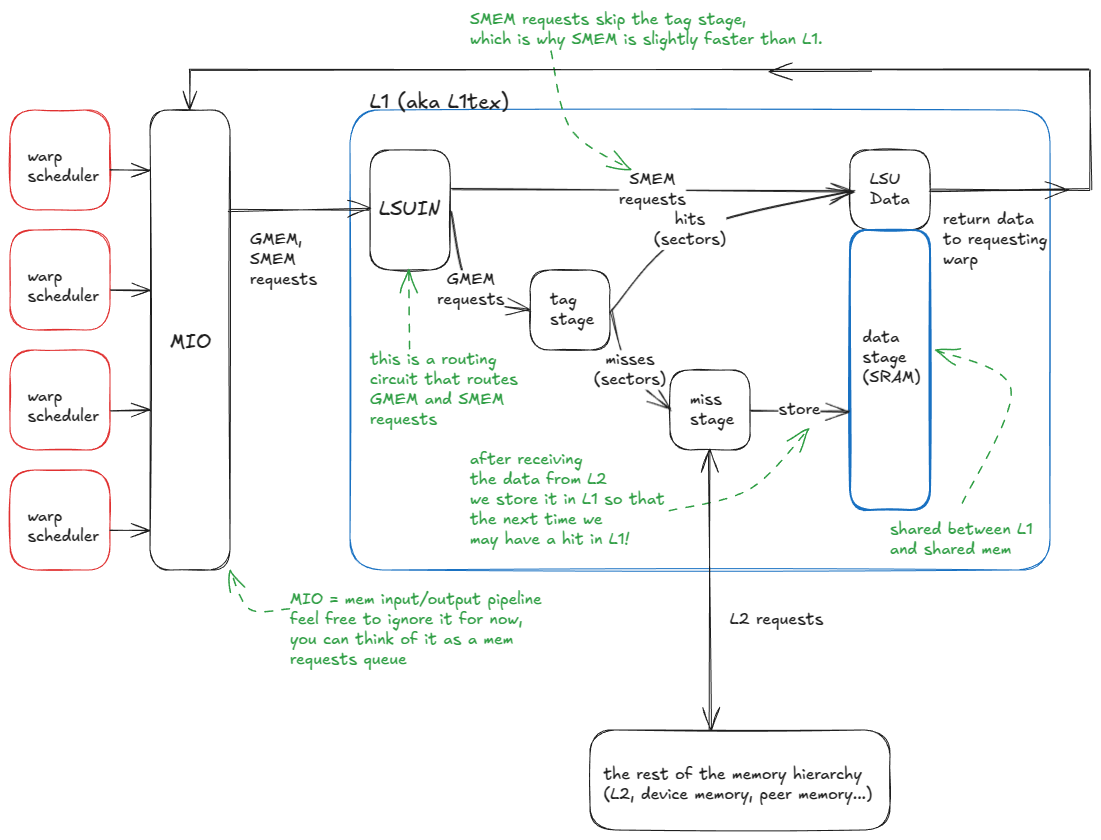
图 13：L1 缓存模型

图 13：L1 缓存模型

让我们深入一层，详细查看标签阶段和数据阶段：

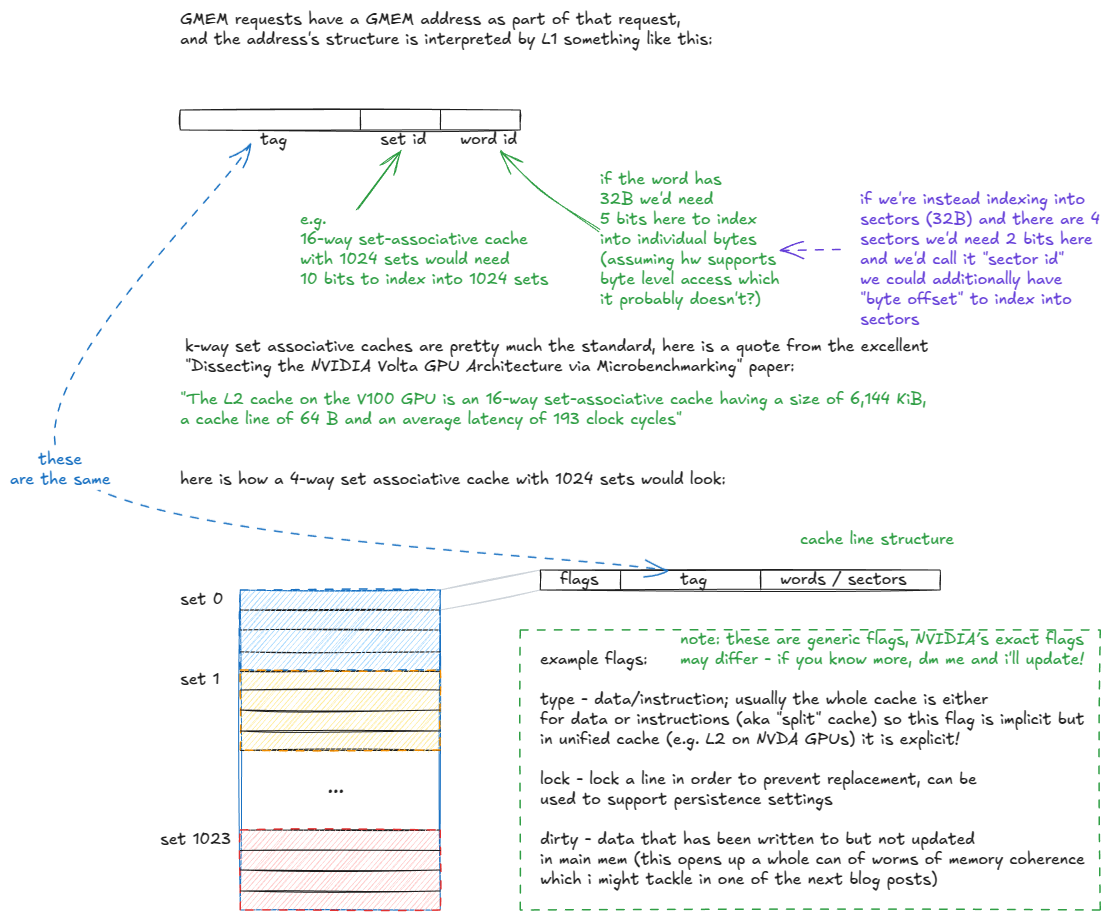
图 14：k 路组关联缓存组织的分解

图 14：k 路组关联缓存组织的分解

当 GMEM 地址进入标签阶段时，命中/未命中逻辑展开如下：

标签阶段接收 GMEM 地址。
提取集合 ID 位，并检查该集合中的所有缓存行（标签）。
如果找到标签匹配（潜在缓存命中）：
- 检查行的有效性标志。
  - 如果无效→视为缓存未命中（继续步骤 4）。
  - 如果有效→从数据数组获取请求的扇区并传递到 warp 的寄存器。
如果未找到匹配（缓存未命中），请求将被路由到内存层次结构的其余部分（L2 及更高层级）。
- 当数据从 L2 返回时，它被存储在集合中，根据替换策略（例如，伪 LRU）驱逐现有行，并并行地交付给请求的 warp。

请注意，L2 与 L1 并无太大不同，除了它是全局的（相对于每个 SM）、更大（具有更高的关联度）、划分为两个通过交叉开关连接的切片，并支持更细致的持久性和缓存策略。

至此，我们已经涵盖了理解后续章节所需的关键 GPU 硬件组件。

📝GPU 代际间的梯度：

我之前提到，理解 Hopper 是理解 NVIDIA GPU 未来和过去代际的绝佳基础。

迄今为止最大的代际跃迁是从 Ampere → Hopper，引入了：

分布式共享内存（DSMEM）：用于在整个 GPC 的 SMEM 之间进行直接 SM 到 SM 通信，支持加载、存储和原子操作。
TMA：用于异步张量数据移动的硬件单元（GMEM ↔ SMEM, SMEM ↔ SMEM）。
线程块集群：一种新的 CUDA 编程模型抽象，用于跨 SM 分组块。
异步事务屏障：分割屏障，计数事务（字节）而不仅仅是线程。

Ampere（例如 A100）本身引入了几个关键特性：

Tensor Core 中的 tf32 和 bf16 支持。
异步复制（GMEM → SMEM），具有两种模式：绕过 L1 和访问 L1。
异步屏障（在共享内存中硬件加速）。
CUDA 任务图，支撑 PyTorch 中的 CUDA 图，并减少 CPU 启动和网格初始化开销。
通过 CUDA Cooperative Groups 暴露的 warp 级归约指令（支持 warp 范围内、整数数据类型的单步归约，无需 shuffle 模式）。

GPU 汇编语言：PTX 和 SASS¶

让我们向上移动一个层级到 ISA（指令集架构）。ISA 简单来说就是处理器（例如，NVIDIA GPU）可以执行的指令集合，包括它们的二进制编码（操作码、操作数等）和行为语义。这些共同定义了程序员如何指导硬件执行有用工作。

ISA 的人类可读形式被称为汇编：程序员使用助记符如0x1fff…3B，而不是像FMA R12, R13, R14, R15那样编写原始二进制。

在 NVIDIA GPU 上，原生 ISA 称为 SASS。不幸的是，它的文档很少——尤其是对于最新的 GPU 代际。一些较旧的代际已被部分或完全逆向工程，但官方文档仍然有限。您可以在此处 here [6] 找到文档。

PTX 是 NVIDIA 的虚拟 ISA：一种抽象 GPU 的指令集。PTX 代码不直接执行；而是由ptxas编译为原生 ISA（SASS）。

PTX 的关键优势是前向兼容性。十年前编译为 PTX 的 CUDA 程序仍然可以在现代 GPU 如 Blackwell 上运行。它可能无法高效利用最新的硬件特性，但会正确执行。

这是因为 PTX 被嵌入到 CUDA 二进制文件中，与原生 SASS 一起。当二进制文件在未来 GPU 上运行时，如果匹配的 SASS 代码不存在，PTX 会被 JIT 编译为目标架构的 SASS：

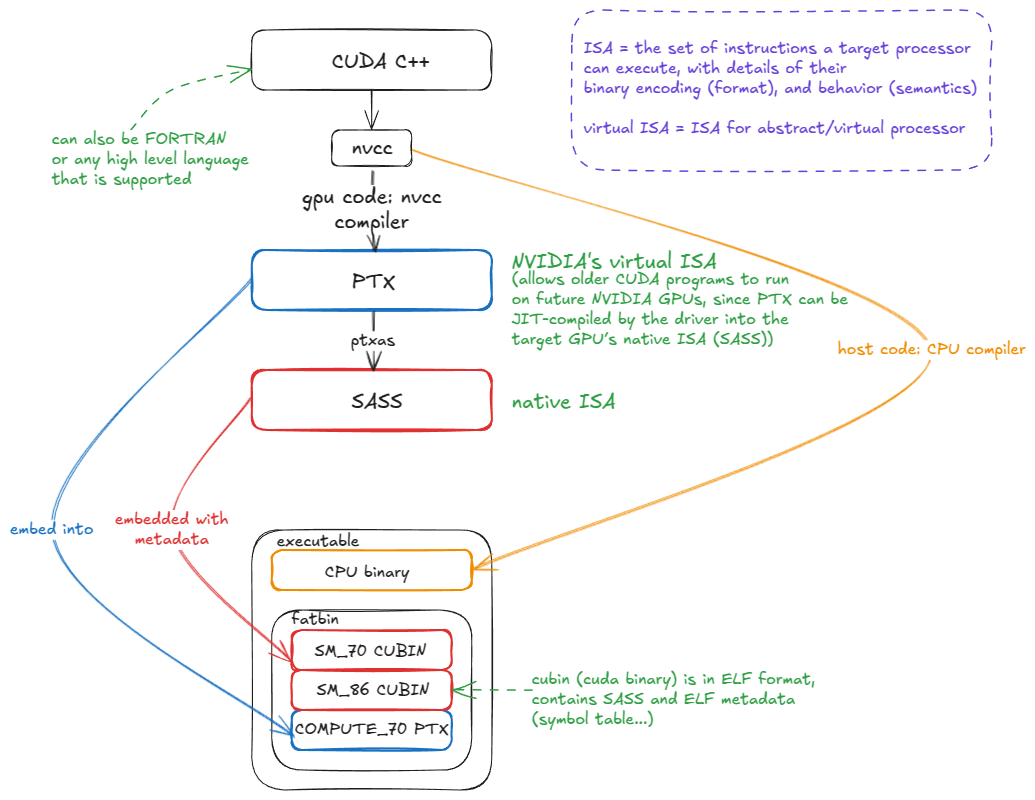
Figure 15: CUDA compilation flow: from CUDA C++ → PTX → SASS

图 15：CUDA 编译流程：从 CUDA C++ → PTX → SASS

为什么关心 PTX/SASS？

因为这是可以找到最后几个百分点性能的地方。在今天的规模下，这些“几个百分点”是巨大的：如果您在 30,000 个 H100 上训练 LLM，即使将核心内核性能提高 1%，也能节省数百万美元。

正如我的朋友 Aroun 喜欢说的：在编写大规模训练/推理内核时，我们关心O(NR)，而不是O(N)。（这里，NR = 核反应堆。）换句话说，可能没有新的渐近复杂度类等待被发现——大的收益（大部分）已经消失。但在数百万 GPU 上挤出约 1%的效率，相当于节省几个 SMR（小型模块化反应堆）的能量。

要深入了解 SASS，我推荐 Aroun 的 “Introduction to SASS & GPU Microarchitecture” [7] 视频。

理解 SASS 并不意味着您将开始直接用 SASS 编写 CUDA 内核。相反，在编写 CUDA C++时，您希望与编译器的输出（PTX/SASS）保持紧密耦合。这可以让您双重检查您的提示（例如，#pragma unroll用于展开循环，或向量化加载）是否确实被降低为预期的指令（例如，LDG.128）。

这些低级细节中隐藏性能的一个很好例子来自现在著名的 Citadel 论文，“Dissecting the NVIDIA Volta GPU Architecture via Microbenchmarking” [8]。作者调整 SASS 以避免内存 bank 冲突，并将性能从 132 GFLOP/s 提升到 152 GFLOP/s——提高了 15.4%。

还要注意，一些指令在 CUDA C++中没有等效项；您只需编写内联 PTX！我们将在第 4 章后面看到这方面的例子。

现在（希望）我已经说服您 PTX/SASS 很重要，让我们介绍最简单的 matmul 内核，它将作为本章剩余部分的运行示例。之后，我们将深入分析其汇编。

让我们从最简单的情况开始：一个针对“串行处理器”如 CPU 的朴素矩阵乘法内核：

for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n++) {
        float tmp = 0.0f;  // accumulator for dot product
        for (int k = 0; k < K; k++) {
            tmp += A[m][k] * B[k][n];  // A and B are input matrices
        }
        C[m][n] = tmp;  // C is the output matrix
    }
}

for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n++) {
        float tmp = 0.0f;  // accumulator for dot product
        for (int k = 0; k < K; k++) {
            tmp += A[m][k] * B[k][n];  // A and B are input matrices
        }
        C[m][n] = tmp;  // C is the output matrix
    }
}

我们循环遍历输出矩阵（m）的行（n）和列（C），并在每个位置计算点积（C[m,n] = dot(a[m,k],b[k,n])）。这是 matmul 的教科书定义：

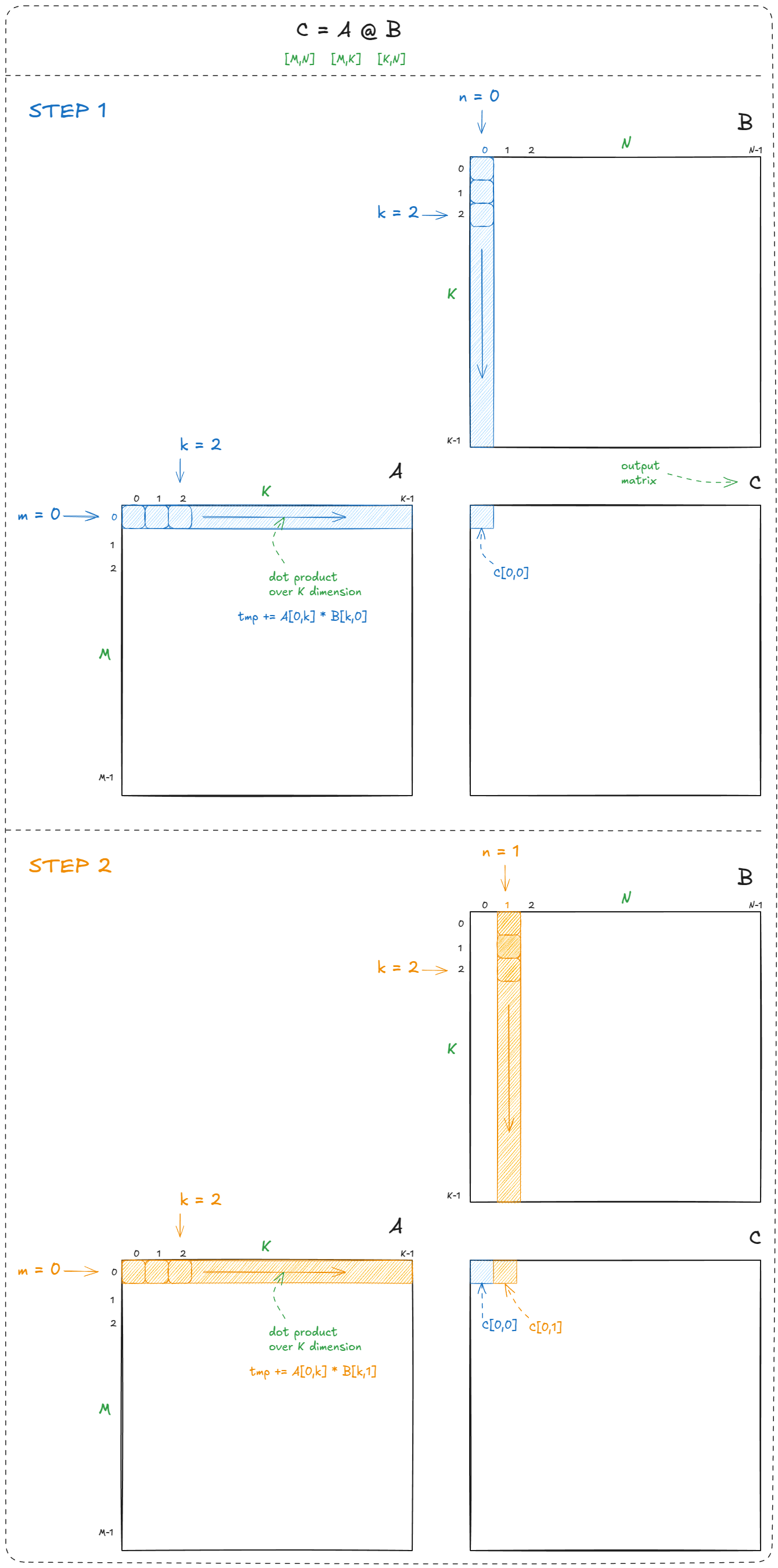
Figure 16: Naive CPU matmul example

图 16：朴素 CPU matmul 示例

总的来说，矩阵乘法需要M × N个点积。每个点积执行K次乘加，所以总工作量是2 × M × N × K FLOPs（因子 2 是因为，按照惯例，我们计数 FMA = 乘法 + 加法）。

并行性在哪里？

所有这些点积都是独立的。没有理由计算C[0,1]应该等待C[0,0]。这种独立性意味着我们可以跨两个外部循环（遍历m和n）进行并行化。

基于这一见解，让我们看看最简单的 GPU 内核。我们将使用一个稍微更通用的形式：C = alpha * A @ B + beta * C。这是经典的 GEMM（通用矩阵乘法）。设置alpha = 1.0和beta = 0.0可以恢复更简单的C = A @ B。

内核代码：

// __global__ keyword declares a GPU kernel
__global__ void naive_kernel(int M, int N, int K, float alpha,
                                          const float *A, const float *B,
                                          float beta, float *C) {
  int BLOCKSIZE=32;
 
  const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);
  const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);
 
  if (row < M && col < N) {  // guard in case some threads are outside the range
    float tmp = 0.0;
    // compute dot product
    for (int i = 0; i < K; ++i) {
      tmp += A[row * K + i] * B[i * N + col];
    }
    // GEMM: C = alpha * A @ B + beta * C
    C[row * N + col] = alpha * tmp + beta * C[row * N + col];
  }
}

// __global__ keyword declares a GPU kernel
__global__ void naive_kernel(int M, int N, int K, float alpha,
                                          const float *A, const float *B,
                                          float beta, float *C) {
  int BLOCKSIZE=32;
 
  const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);
  const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);
 
  if (row < M && col < N) {  // guard in case some threads are outside the range
    float tmp = 0.0;
    // compute dot product
    for (int i = 0; i < K; ++i) {
      tmp += A[row * K + i] * B[i * N + col];
    }
    // GEMM: C = alpha * A @ B + beta * C
    C[row * N + col] = alpha * tmp + beta * C[row * N + col];
  }
}

我们这样启动它：

// create as many blocks as necessary to map all of C
dim3 gridDim(CEIL_DIV(M, 32), CEIL_DIV(N, 32), 1);
// 32 * 32 = 1024 thread per block
dim3 blockDim(32 * 32);
// launch the asynchronous execution of the kernel on the device
// the function call returns immediately on the host
naive_kernel<<<gridDim, blockDim>>>(M, N, K, alpha, A, B, beta, C);

// create as many blocks as necessary to map all of C
dim3 gridDim(CEIL_DIV(M, 32), CEIL_DIV(N, 32), 1);
// 32 * 32 = 1024 thread per block
dim3 blockDim(32 * 32);
// launch the asynchronous execution of the kernel on the device
// the function call returns immediately on the host
naive_kernel<<<gridDim, blockDim>>>(M, N, K, alpha, A, B, beta, C);

你可以在这里观察到几点：

内核是从单个线程的角度编写的。这遵循 SIMT（单指令多线程）模型：程序员编写一个线程的工作，而 CUDA 处理网格、集群和块的启动和初始化。（其他编程模型，如 OpenAI 的 Triton [22]，让你从tile的角度编写。）
每个线程使用其块和线程索引（我们之前讨论的变量）来计算其在row中的（col，C）坐标，并写出相应的点积。
我们使用尽可能多的 32×32 线程块（1024 个线程）来平铺输出矩阵。
如果M或N不能被 32 整除，一些线程会落在C的有效输出区域之外。这就是为什么我们在代码中包含一个保护条件。

最后两点结合导致了一个通常被称为tile quantization：

Figure 17: Tile quantization

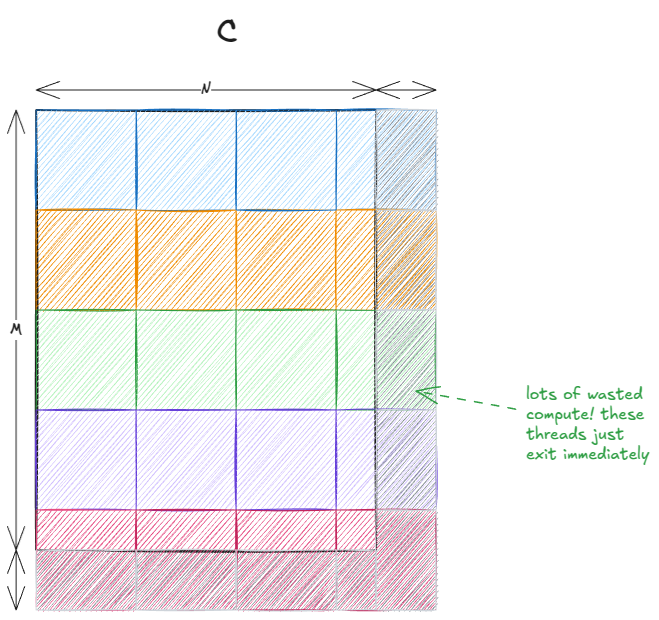
图 17：Tile quantization

当 tile 相对于输出矩阵较大时，这种效应尤其明显。在我们的例子中，由于 32 能整除 4096，所以没有问题。但如果矩阵大小是，比如 33×33，那么大约 75%的线程最终会做无用功。

代码本可以通过传递 2D 块而不是 1D 块来更简单地编写。那样的话，我们就不需要硬编码块大小为 32，并且可以使用threadIdx.x和threadIdx.y。在内部，1D 结构通过索引算术有效地转换为 2D：threadIdx.x / BLOCKSIZE和threadIdx.x % BLOCKSIZE，所以在实践中差别不大。

我最初从 Simon 的博客 [9] 改编了这段代码，并专注于对其进行深入的 PTX/SASS 分析（即将到来），所以我不想重复辛苦工作，因为轻微的代码更改会导致不同的 PTX/SASS。

让我们更仔细地看看这个内核实际上做了什么。在本文的其余部分，我们将假设M = N = 4096。本示例中的所有矩阵都是行主序格式（在一些后续示例中，B将是列主序 - 标准约定）。

线程的逻辑组织如下所示：

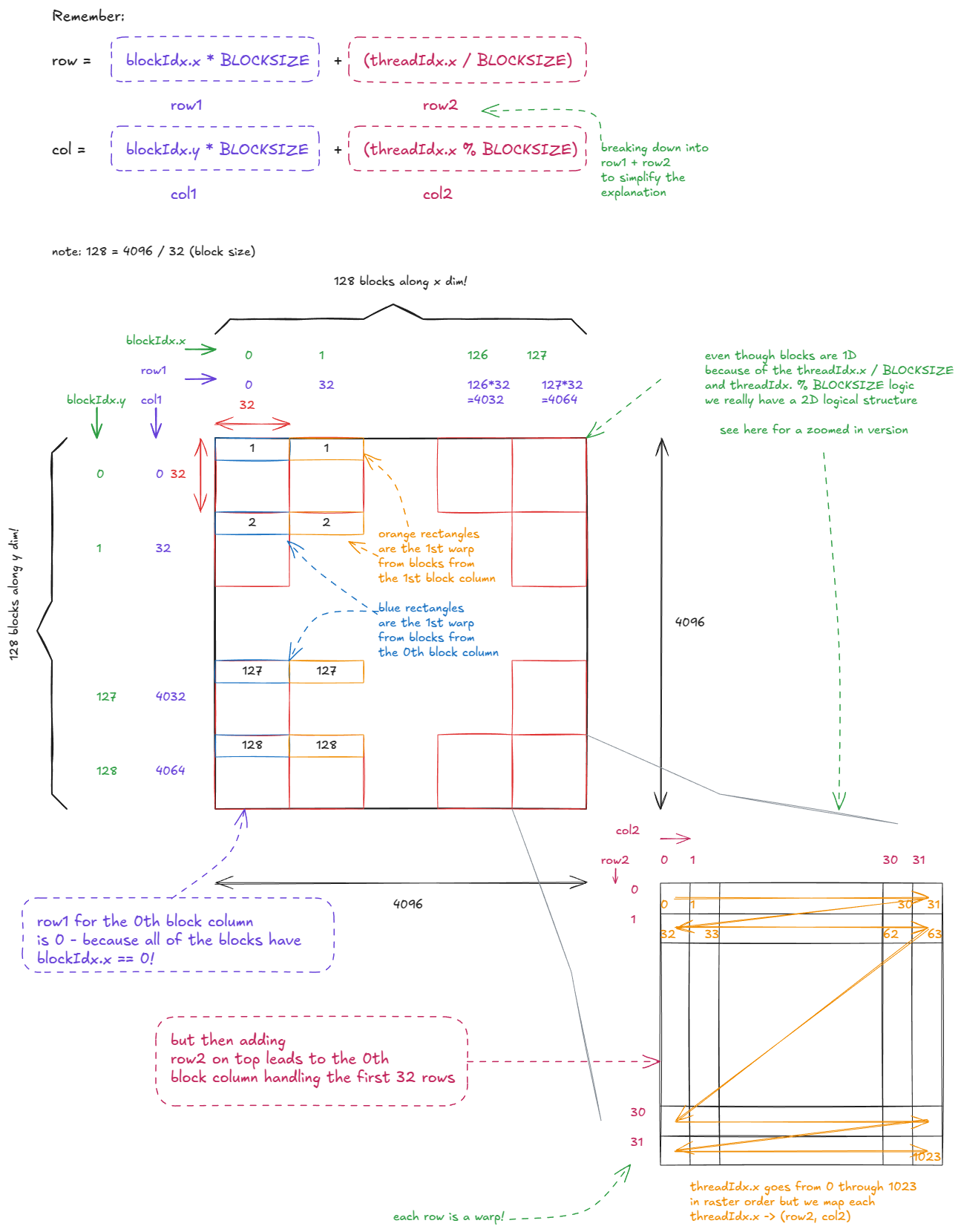
Figure 18: Thread organization in naive matmul kernel

图 18：朴素矩阵乘法内核中的线程组织

矩阵乘法逻辑本身如下所示：

Figure 19: Naive matmul kernel

图 19：朴素矩阵乘法内核

当我们的 GMEM 访问是合并的时，硬件中会自动发生一些有趣的优化：

（矩阵 A）对于一个 warp 从A读取，32 个每线程LDG.32指令（全部来自同一地址）合并为一个 warp 级别的LDG.32，其结果广播到 warp 中的所有线程。
（矩阵 B）对于一个 warp 从B读取，32 个连续的每线程LDG.32指令组合为一个 128B 的 warp 级别加载。这依赖于线程沿着连续维度读取。如果它们读取列（非连续），硬件将需要发出多个 warp 级别指令。

注意，我们总共启动了 (4096/32) * (4096/32) = 16,384 个线程块。然而，H100 PCIe（我使用的卡）只有 114 个 SM。

这引出了一个问题：每个 SM 上可以同时运行多少个块？

一般来说，三种资源限制并发性：

寄存器
共享内存（SMEM）
线程/warp

从 Nsight Compute 分析器（ncu --set full -o out.ncu-rep naive_kernel，也见下图），我们看到内核每个线程使用 32 个寄存器。每个块有 1024 个线程，那就是每个块 1024×32=32,768 个寄存器。由于每个 SM 有 65,536 个寄存器（你可以在 CUDA C 编程指南 [10] 中找到这些常量），这限制我们每个 SM 最多 2 个块。

📝注意：

提示。你也可以在编译时传递--ptxas-options=-v让编译器报告寄存器使用情况和其他资源计数。nvdisasm也是一个有用的小工具。

在 Hopper（计算能力 9.0）上，每个 SM 的最大线程数是 2048。每个块有 1024 个线程，这再次限制我们每个 SM 最多 2 个块。

回想硬件章节，即使内核没有显式使用 SMEM，每个块总是有 1024B 的系统级开销。在默认的 SMEM 分配为每个 SM 8192B（不将拨盘调到 228 KiB）的情况下，这将允许最多 8 个块。

综合起来：max blocks/SM = min(2,2,8) = 2。

所以，在任何给定时间，这个内核在 GPU 上最多可以有 114×2 = 228 个线程块驻留。

这意味着我们需要 16,384 / 228 = ~71.86 个所谓的waves来完成矩阵乘法操作。

📝占用率

在 CUDA 术语中，占用率通常指可以在 SM 上同时运行的块数。还有一个密切相关的定义：

占用率（warp）：活动 warp 与每个 SM 最大 warp 数的比率。

这里，“活动 warp”指线程块在启动时分配资源（寄存器、SMEM 等）后的 warp。

Figure 20: Nsight Compute: Occupancy, Waves info

图 20：Nsight Compute：占用率、Waves 信息

这里有一个优秀教程 [11] 关于使用 Nsight Compute 分析器。

值得在这里提到：就像tile quantization一样，也有一个wave quantization的概念。当 wave 数量较小时，这种效应尤其明显。

例如，假设我启动一个内核，有 114 个块（正好是我的 H100 PCIe 上的 SM 数）。并假设我们一次只能运行 1 个块/SM。每个 SM 只有一个块，内核在一个 wave 中完成。现在想象我将启动增加到 115 个块。突然，执行时间几乎翻倍——因为我们需要两个 wave——但第二个 wave 中的大部分资源闲置，只有一个块运行：

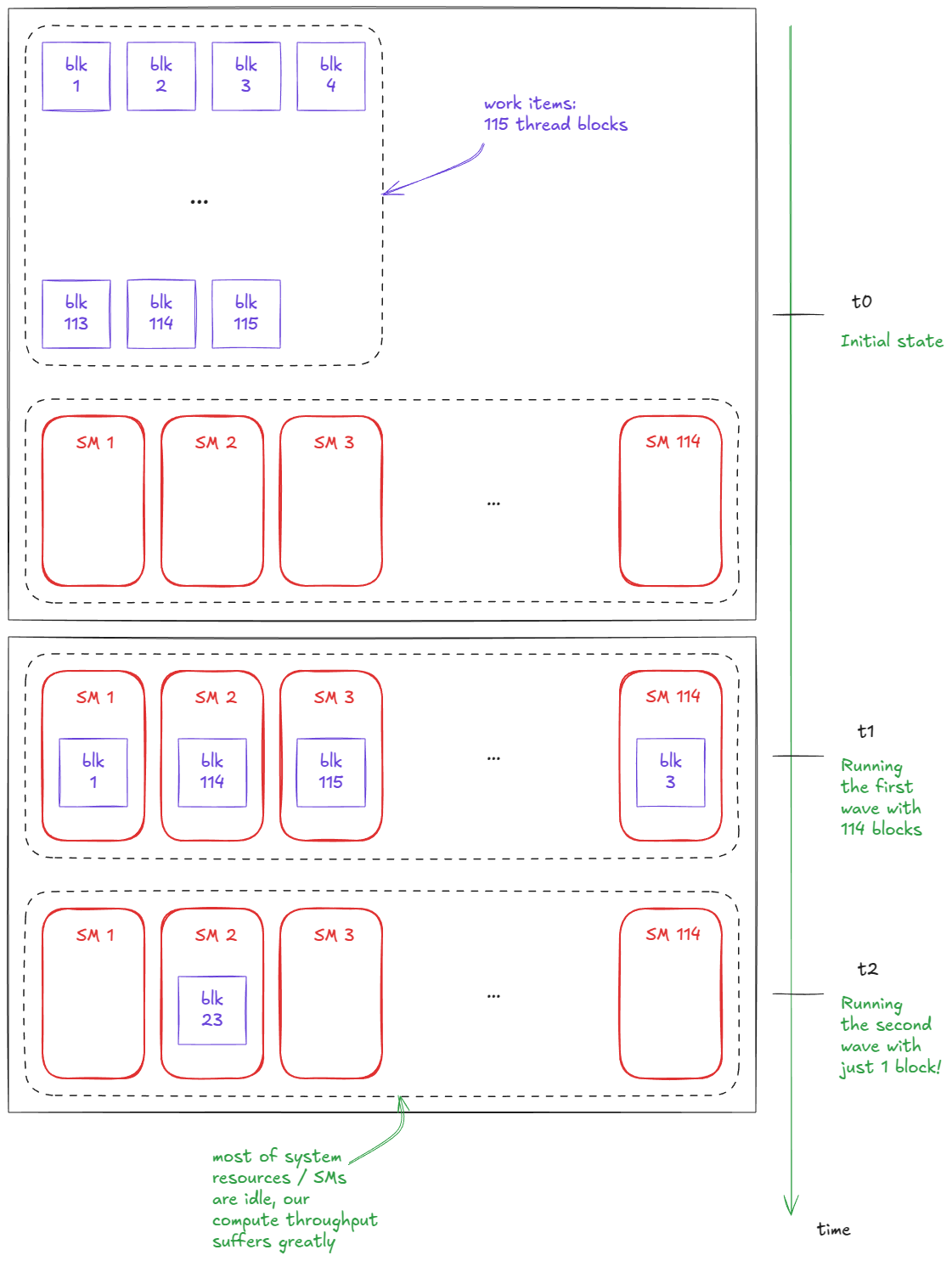
Figure 21: Wave quantization

图 21：Wave quantization

有了对朴素矩阵乘法内核的基本分析，现在让我们转向 PTX/SASS 视图。以下是我使用的编译设置（Godbolt）：

compilation settings:
nvcc 12.5.1

-O3  # the most aggressive standard-compliant optimization level, add loop unrolling, etc.
-DNDEBUG  # turn assert() into noop, doesn't matter for our simple kernel
--generate-code=arch=compute_90,code=[compute_90,sm_90a]  # embed PTX/SASS for H100
--ptxas-options=-v  # makes ptxas print per-kernel resource usage during compilation
-std=c++17  # compile the code according to the ISO C++17 standard, doesn't matter
# --fast-math  # not using, less important for this kernel

compilation settings:
nvcc 12.5.1

-O3  # the most aggressive standard-compliant optimization level, add loop unrolling, etc.
-DNDEBUG  # turn assert() into noop, doesn't matter for our simple kernel
--generate-code=arch=compute_90,code=[compute_90,sm_90a]  # embed PTX/SASS for H100
--ptxas-options=-v  # makes ptxas print per-kernel resource usage during compilation
-std=c++17  # compile the code according to the ISO C++17 standard, doesn't matter
# --fast-math  # not using, less important for this kernel

另一个重要设置是--use_fast_math。它用速度换取数值精度，主要影响 fp32 操作。例如，它将标准数学函数替换为快速、近似的内部函数（例如sinf

__sinf），启用对非规格化数（低于最小“规格化”可表示幅度的极小浮点数）的归零（ftz）等。

以下是上面展示的 CUDA C++内核的带注释 PTX。我手动解码它以更好地内化 ISA。请随意放大并花点时间消化结构（或者直接跳到图表后阅读我的摘要，然后返回图表）：

Figure 22: PTX code corresponding to naive matmul CUDA kernel

图 22：对应朴素矩阵乘法 CUDA 内核的 PTX 代码

总结一下，以下是 PTX 代码的高级流程：

计算row和col变量。有趣的是，编译器使用bfi（位域插入）指令来计算col，而不是简单地将寄存器r2和r3相加。这可能是通过将工作路由到利用率较低单元来平衡执行流水线的尝试——但请注意，bfi本身并不比加法指令快。
如果此线程超出C的有效范围，则提前退出（保护逻辑）。
如果K < 1，直接跳转到存储到C（tmp将为 0.0）。
如果K <= 3，跳转到尾部循环。
否则，如果K > 3：在进入主循环前计算A和B的基础偏移。
主循环（展开×4）。每次迭代执行 4 个 FMA 步骤，与加载和地址算术交错进行。
尾部循环（<= 3次迭代）。执行剩余的向量点积步骤，不展开。
尾声：加载C的输出值，应用 GEMM 更新（alpha * A @ B + beta * C），并使用st.global.f32将结果写回全局内存。

这里可以看到一些编译器优化：提前退出、循环展开、分割为主循环和尾部循环，以及看起来像流水线负载平衡（假设我的bfi假设正确）。

展开尤其重要，因为它暴露了 ILP（指令级并行性）。warp 不需要那么快被换出，因为它仍有独立指令可发出——这有助于隐藏延迟。

什么是 ILP（指令级并行性）？

指令级并行性（ILP）是单个 warp 通过连续发出独立指令能同时保持“在飞行中”的工作量。高 ILP 让 warp 调度器能在每个周期发出新指令，而较早的指令仍在等待其延迟。

考虑这两个指令流（假设 FMA 需要 4 个周期）：

1) 低 ILP（完全依赖链）

y = a * b + 1.0;     // uses a,b
z = y * c + 1.0;     // depends on y
w = z * c + 1.0;     // depends on z

y = a * b + 1.0;     // uses a,b
z = y * c + 1.0;     // depends on y
w = z * c + 1.0;     // depends on z

每个 FMA 依赖于前一个结果 => 无法并行调度 => 总延迟 = 12（3*4）个周期。

2) 高 ILP（独立操作）

c0 = a0 * b0 + 1.0;
c1 = a1 * b1 + 1.0;
c2 = a2 * b2 + 1.0;

c0 = a0 * b0 + 1.0;
c1 = a1 * b1 + 1.0;
c2 = a2 * b2 + 1.0;

三个独立 FMA => 调度器可以在连续周期发出它们。在周期 0、1、2 发出，结果在 4、5、6 就绪 => 总延迟 = 6 个周期。

这就是为什么循环展开/ILP 很重要。

对于调试，您可能想禁用循环展开以使 PTX/SASS 分析更容易。只需添加：#pragma unroll 1。

展开还减少了分支（bra）指令的数量，使程序更简洁/高效。

我还观察到一些编译器低效之处，例如：

不必要地将变量初始化为 0。
过于复杂地计算A的地址。
冗余的部分偏移计算，其中两个指令本可合并为一个。

有趣！现在让我们看看对应的 SASS 代码：

Figure 23: SASS code corresponding to naive matmul CUDA kernel

图 23：对应朴素矩阵乘法 CUDA 内核的 SASS 代码

我只强调与 PTX 代码的差异：

循环现在展开×16！
LDG 指令移到循环顶部，将计算与数据加载重叠。FMA 大多聚集在每个展开块的末尾。
有 2 个尾部循环：一个展开 8 倍，一个展开 4 倍，最终循环覆盖最后 3 次迭代。

我在 SASS 中也发现了有趣的编译器怪癖和低效之处：

程序计数器（R1寄存器）被加载但从未使用。原因不明？
冗余的零初始化仍然存在。
一个谓词是空操作：它总是为真，所以跳转到标签L_x_2（4 倍展开循环）从未执行。
4 倍展开循环包含一个多余的BRA指令——它永远不会迭代超过一次。
在最终EXIT之后，代码陷入无限 while 循环。是虚假的实现细节还是故障？
最后（不是故障），代码用NOPs填充以实现内存对齐。

有趣！我们感受到了编译器在幕后做了什么。

现在，有了所有这些背景知识，让我们换个档，深入一些 SOTA（最先进）内核。

📝下一章的补充阅读：

我强烈推荐 Simon 的优秀博客文章。它是我最初深入内核的灵感来源。在本章中，我将使用他的内核 10 [12] 代码作为参考。虽然代码本身似乎是基于 CUTLASS 的（参见这个 [13] 和这个 [14] 例如），但我首先分析了 Simon 的版本——所以这里我将遵循那个版本。

设计接近 SOTA 的同步矩阵乘法内核¶

在本章中，我们将分解一个在以下约束下接近 SOTA 的 fp32 内核：

无 TMA（张量内存加速器）
无异步内存指令
无张量核心
仅 fp32（无 bf16）

换句话说，这是在 Volta 前 GPU 模型下的 SOTA（在 Volta/Ampere 上接近 SOTA）：

Volta 引入了张量核心
Ampere 引入了异步内存指令
Hopper 引入了 TMA

我们将研究的技术称为warp-tiling（warp 平铺）。

在深入之前，让我们用一个小修改重新审视之前的内核，看看会发生什么。具体来说，我们将改变row和col变量的计算方式。

原始版本：

const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);
const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);

const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);
const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);

修改版本：

const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);
const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);

const int row = blockIdx.x * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);
const int col = blockIdx.y * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);

换句话说，我们只是交换了%和/运算符。

交换row2和col2是与之前示例相比逻辑结构中的唯一变化：

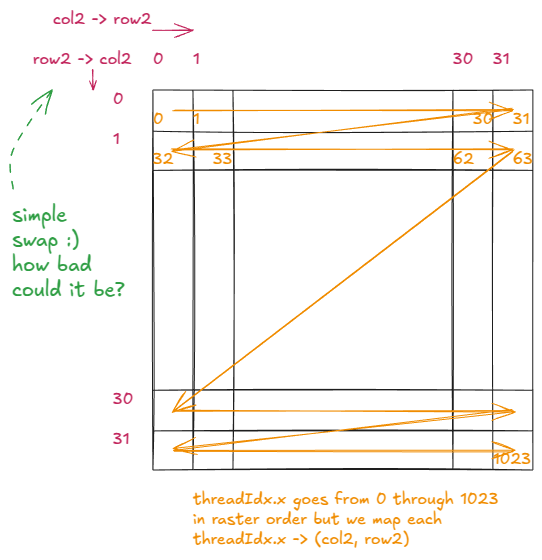
Figure 24: New logical organization of row2 and col2 variables

图 24：row2 和 col2 变量的新逻辑组织

这是修改后内核现在所做的：

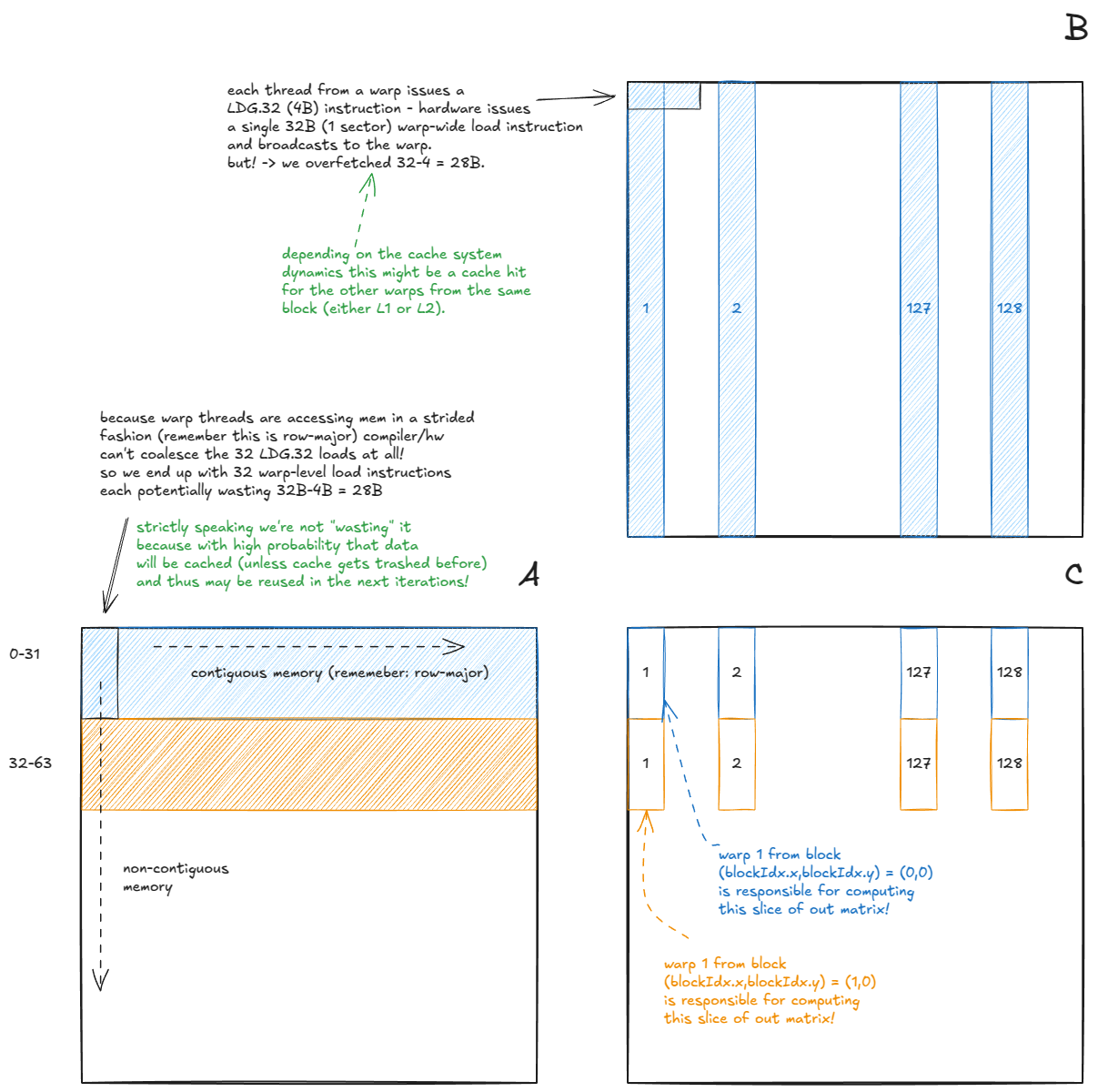
Figure 25: Naive kernel with uncoalesced GMEM access

图 25：具有非合并 GMEM 访问的朴素内核

这个看似无害的调整使我们的 GMEM 访问非合并。

在我的 H100 PCIe 卡上，性能从 3171 GFLOP/s 下降到仅 243 GFLOP/s——13 倍的减速。这正是我们在 GMEM 部分（Stephen Jones 的步进式 GMEM 访问实验）中看到的惩罚类型。

从外部看，这似乎只是两个运算符之间的简单交换。但如果你没有硬件的心理模型，你绝不会预料到如此戏剧性的效果。

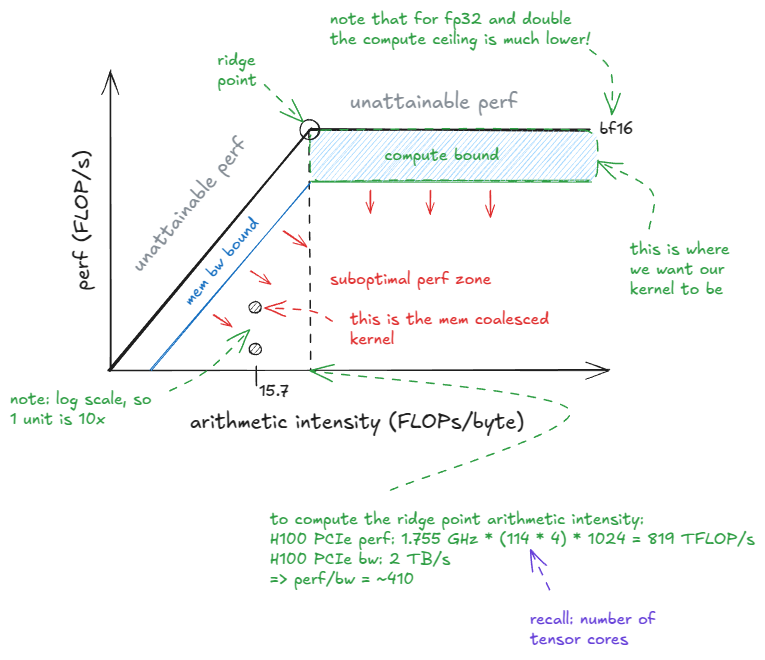
图 26：屋顶线模型

图 26：屋顶线模型

查看屋顶线模型，你可以看到我们的内核位于图中内存带宽受限区域的深处。我们为计算支付 NVIDIA 大笔费用，所以不妨瞄准计算受限区域。

📝屋顶线模型

屋顶线模型绘制性能（FLOP/s）在 y 轴上，对应算术强度（AI）在 x 轴上。

算术强度定义为每个从设备内存/GMEM（默认）加载的字节执行的 FLOP 数量。

“脊点”出现在：peak perf / GMEM bw。对于我的 H100 PCIe，这大约是 ~410。只有当 AI 超过此值时，内核才能进入计算受限状态。

在继续之前，让我们重新审视顺序矩阵乘法代码。作为参考：

for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n++) {
        float tmp = 0.0f;  // accumulator for dot product
        for (int k = 0; k < K; k++) {
            tmp += A[m][k] * B[k][n];
        }
        C[m][n] = tmp;
    }
}

for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n++) {
        float tmp = 0.0f;  // accumulator for dot product
        for (int k = 0; k < K; k++) {
            tmp += A[m][k] * B[k][n];
        }
        C[m][n] = tmp;
    }
}

这里我想强调的关键点是，语义对循环顺序是不变的。换句话说，我们可以以 3! = 6 种方式中的任意一种排列三个嵌套循环，结果仍将是正确的矩阵乘法。

在这六种排列中，最有趣的是以K作为最外层循环的排列。（m 和 n 的相对顺序不太重要，所以让我们假设“规范”的m-n顺序）：

for (int k = 0; k < K; k++) {
    for (int m = 0; m < M; m++) {
        float a = A[m][k];  // reuse this load across N (think GMEM access minimization)
        for (int n = 0; n < N; n++) {
            C[m][n] += a * B[k][n];
        }
    }
}

for (int k = 0; k < K; k++) {
    for (int m = 0; m < M; m++) {
        float a = A[m][k];  // reuse this load across N (think GMEM access minimization)
        for (int n = 0; n < N; n++) {
            C[m][n] += a * B[k][n];
        }
    }
}

如果这些加载来自 GMEM，我们通过将A的加载次数从N^3减少到N^2，大约节省了 2 倍的带宽。

但更重要的见解是算法性的：这个版本将矩阵乘法计算为外积的部分和。这个视角对于理解接下来要深入探讨的 warp-tiling 方法至关重要：

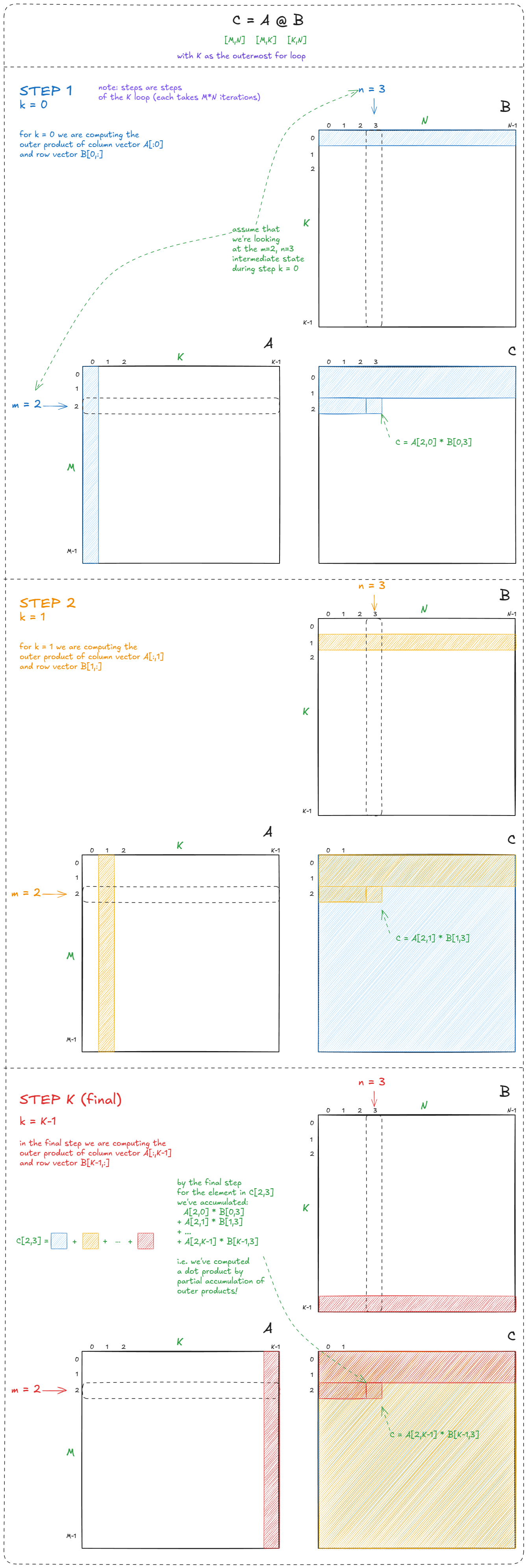
图 27：矩阵乘法作为部分外积的和

图 27：矩阵乘法作为部分外积的和

这可能显而易见，但值得强调：点积等价于部分点积的和：

图 28：点积等价于部分点积的和

图 28：点积等价于部分点积的和

这很重要，因为它让我们将计算分解为一系列块矩阵乘法（每个产生部分点积）。通过在执行计算前将这些块移动到 SMEM，我们可以减少 GMEM 流量并显著加速。

如果不分块，我们不可能将其放入 SMEM。

还要回想，我们的初始内核具有非常低的算术强度——它们每加载的字节做的工作很少。为了改进它，我们需要：

每个线程计算多个输出元素。
使输出瓦片尽可能接近正方形。

这里有一个直观的解释为什么这很重要：

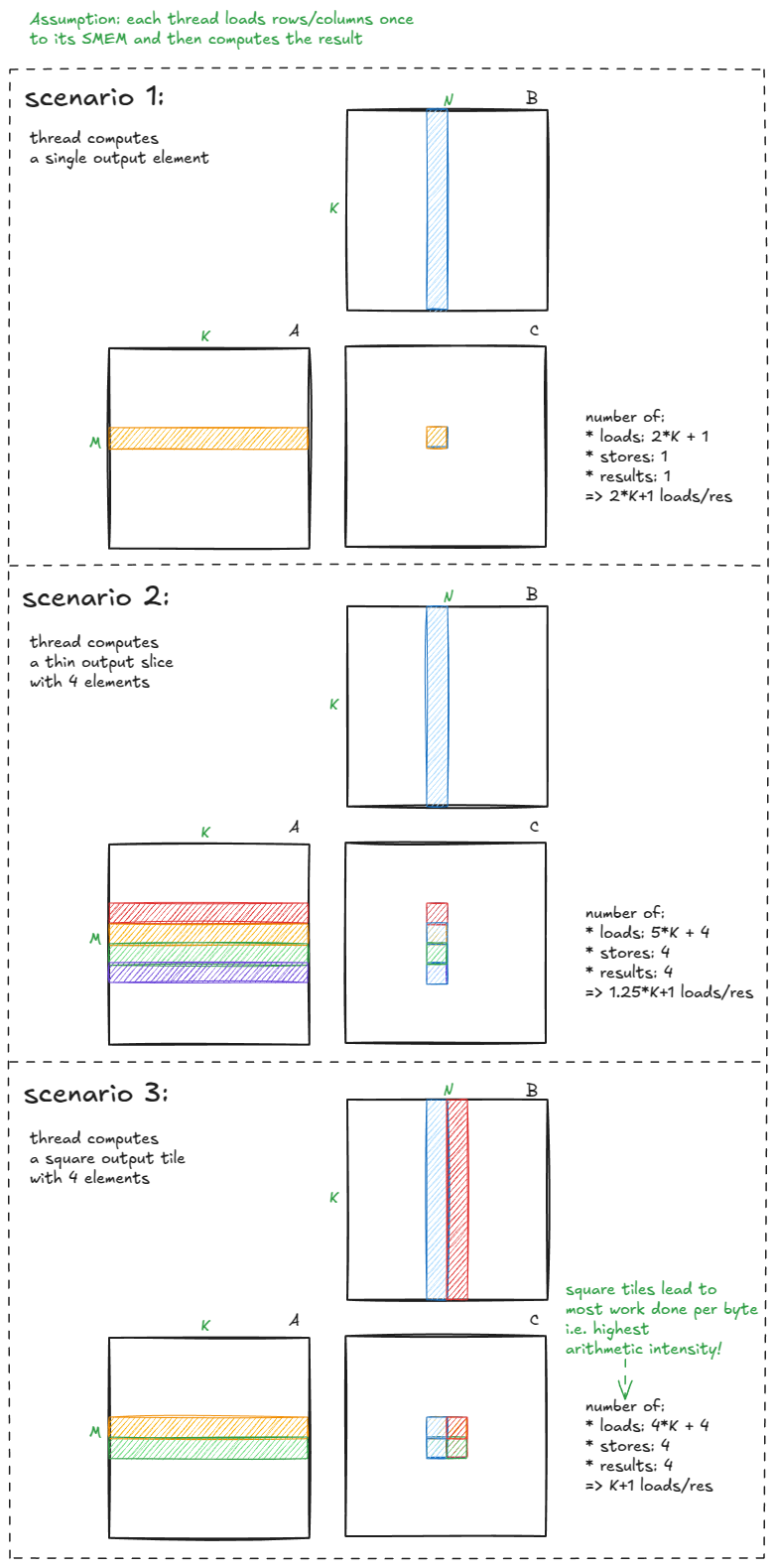
图 29：当每个线程计算多个输出且瓦片接近正方形时，算术强度提高

此时，我们已经收集了理解 warp-tiling 所需的大部分部分。让我们将它们组合起来。

我们知道两个关键点：

输出瓦片应该是正方形的（以最大化算术强度）。
计算应该分解为子步骤，以便中间块可以放入 SMEM。

考虑到这一点，算法的高级结构如下：

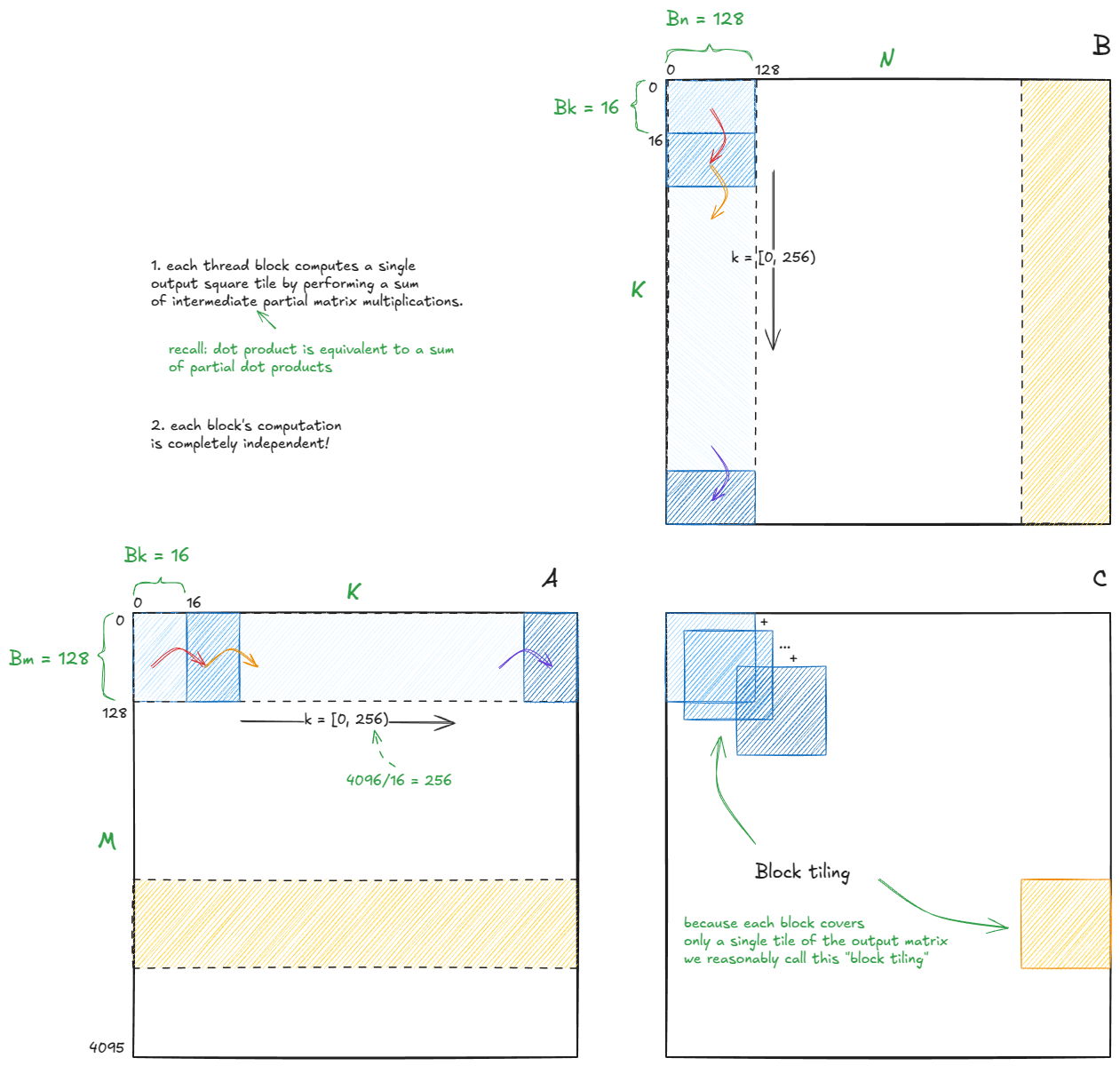
图 30：warp-tiling 算法的高级结构，也称为块瓦片化。

图 30：warp-tiling 算法的高级结构，也称为块瓦片化。

参考代码在这里。我建议从我的图表开始，然后打开代码以连接所有点。

📝注意：

我将使用与 Simon 博客文章中相同的瓦片大小（未针对我的 H100 自动调优）：

Bm = Bn = 128, Bk = 16

由于每个块的计算是独立的——并且我们已经确信部分点积累积为完整点积——我们只需要关注单个块的单个步骤。其余部分（其他 1023 个块，4096/128 * 4096/128 = 32 * 32 = 1024 总计）将遵循相同的逻辑。

📝自我提醒

出于某种原因，我很难忽略其他块。所以，是时候念咒语了：“其他一切都是正确的；我只需要专注于下一步。局部正确性导致全局正确性。” :)

带着这种心态，让我们放大到蓝色块的第一个步骤（红色箭头转换前的计算），对应于输出瓦片C[0,0]（注意 - 瓦片 - 不是元素）。

块维度是Bm × Bk对于矩阵A和Bk × Bn对于矩阵B。这些被加载到 SMEM 缓冲区As和Bs。

加载/存储B到Bs是直接的，因为Bs没有转置。4 个 warps 中的每一个从 GMEM 获取一行B，每个线程发出向量化加载（LDG.128）后跟向量化存储（STS.128）。每个 warp 循环 4 次，步长为 4 行。

对应代码（我添加了注释并移除了 Simon 的注释代码）：

for (uint offset = 0; offset + rowStrideB <= BK; offset += rowStrideB) {
    // we need reinterpret_cast to force LDG.128 instructions (128b = 4 4B floats)
    reinterpret_cast<float4 *>(
        &Bs[(innerRowB + offset) * BN + innerColB * 4])[0] =
        reinterpret_cast<const float4 *>(
            &B[(innerRowB + offset) * N + innerColB * 4])[0];
  }

for (uint offset = 0; offset + rowStrideB <= BK; offset += rowStrideB) {
    // we need reinterpret_cast to force LDG.128 instructions (128b = 4 4B floats)
    reinterpret_cast<float4 *>(
        &Bs[(innerRowB + offset) * BN + innerColB * 4])[0] =
        reinterpret_cast<const float4 *>(
            &B[(innerRowB + offset) * N + innerColB * 4])[0];
  }

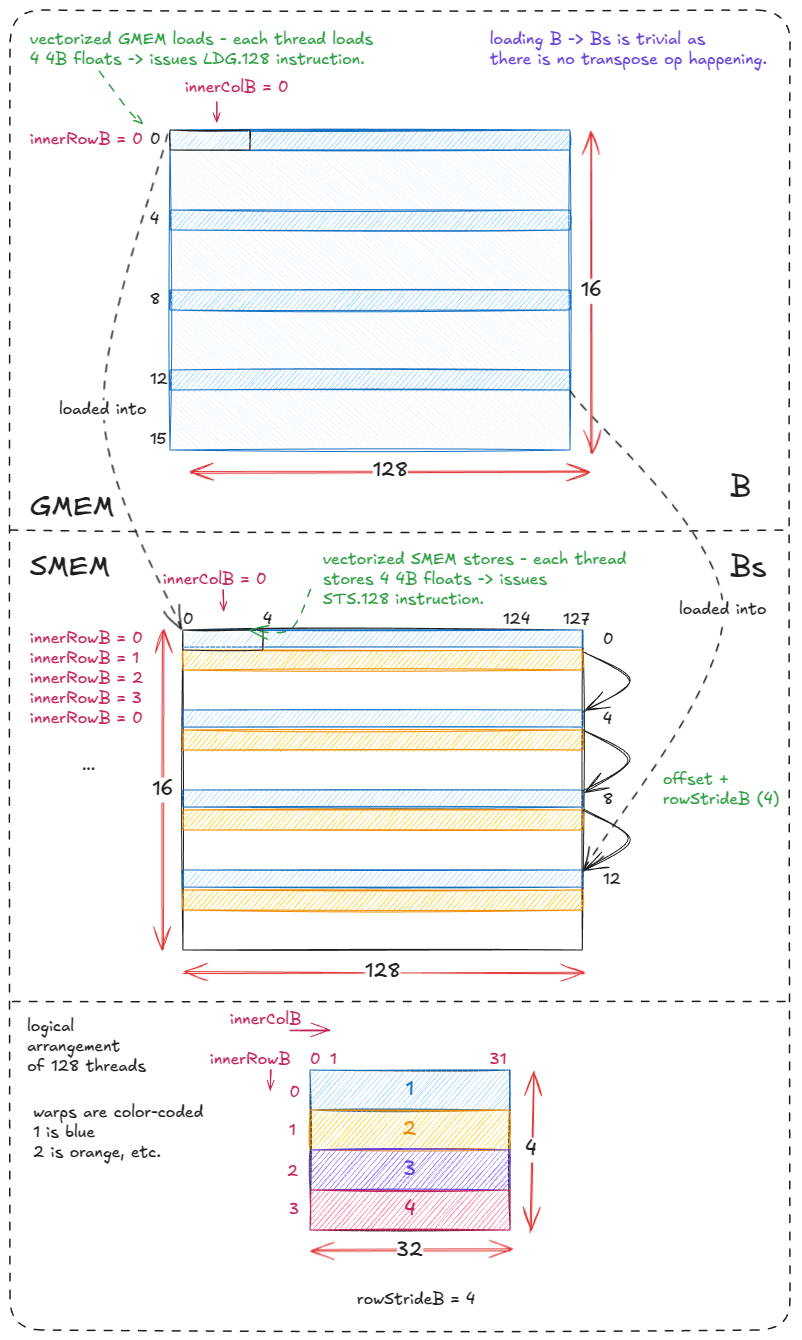
图 31：将 B 的块（GMEM）加载到 Bs（SMEM）

图 31：将 B 的块（GMEM）加载到 Bs（SMEM）

加载A→As。这一步更棘手，因为As是转置的。转置的原因是在计算阶段启用向量化加载（LDS.128）。

权衡是存储不能向量化：从一行A获取的 4 个浮点数现在必须分散到一列As中，这映射到相同的内存库。这是可以接受的，因为我们优先考虑快速加载——As的每个元素在计算期间将被多次访问，而存储只发生一次。

图中的innerRowX和innerColX注释精确显示了每个线程负责的工作。

对应代码：

for (uint offset = 0; offset + rowStrideA <= BM; offset += rowStrideA) {
  // we need reinterpret_cast to force LDG.128 instructions
  const float4 tmp = reinterpret_cast<const float4 *>(
      &A[(innerRowA + offset) * K + innerColA * 4])[0];
  As[(innerColA * 4 + 0) * BM + innerRowA + offset] = tmp.x;
  As[(innerColA * 4 + 1) * BM + innerRowA + offset] = tmp.y;
  As[(innerColA * 4 + 2) * BM + innerRowA + offset] = tmp.z;
  As[(innerColA * 4 + 3) * BM + innerRowA + offset] = tmp.w;
}

for (uint offset = 0; offset + rowStrideA <= BM; offset += rowStrideA) {
  // we need reinterpret_cast to force LDG.128 instructions
  const float4 tmp = reinterpret_cast<const float4 *>(
      &A[(innerRowA + offset) * K + innerColA * 4])[0];
  As[(innerColA * 4 + 0) * BM + innerRowA + offset] = tmp.x;
  As[(innerColA * 4 + 1) * BM + innerRowA + offset] = tmp.y;
  As[(innerColA * 4 + 2) * BM + innerRowA + offset] = tmp.z;
  As[(innerColA * 4 + 3) * BM + innerRowA + offset] = tmp.w;
}

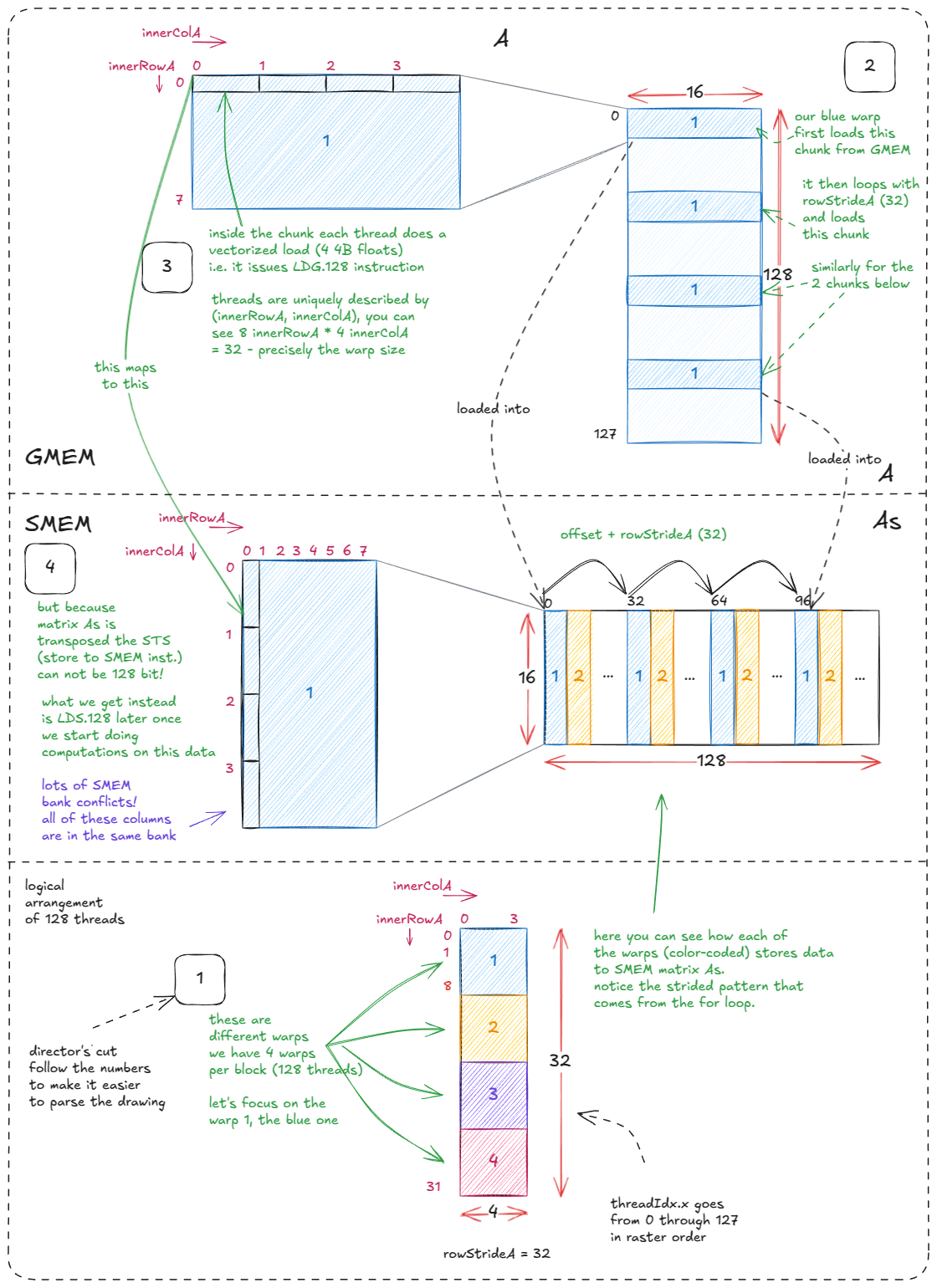
图 32：将 A 的块（GMEM）加载到 As（SMEM）

图 32：将 A 的块（GMEM）加载到 As（SMEM）

加载后，我们同步线程块（__syncthreads()）以确保所有数据在As和Bs中可用。

现在是计算阶段。

对应代码（我建议略读它并查看带有几次传递的绘图：））：

for (uint dotIdx = 0; dotIdx < BK; ++dotIdx) {  // dotIdx is the outer most loop
  // WM = 64, that's why As is broken into 2x64 parts
  // TM = 8, that's why thread processes 8 rows from As
  // WMITER = 1, that's why only single slice in As (2 in the appendix of the drawing)
  for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
    // load from As into register regM
    for (uint i = 0; i < TM; ++i) {
      regM[wSubRowIdx * TM + i] =
          As[(dotIdx * BM) + warpRow * WM + wSubRowIdx * WSUBM +
              threadRowInWarp * TM + i];
    }
  }
  // WN = 64, that's why Bs is broken into 2x64 parts
  // TN = 4, that's why 4 columns per slice of Bs
  // WNITER = 4, that's why four slices in Bs
  // WSUBN = WN/WNITER = 16 (used to iterate over slices)
  for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
    for (uint i = 0; i < TN; ++i) {
      // load from Bs into register regN
      regN[wSubColIdx * TN + i] =
          Bs[(dotIdx * BN) + warpCol * WN + wSubColIdx * WSUBN +
              threadColInWarp * TN + i];
    }
  }

  // execute warptile matmul via a sum of partial outer products
  for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
    for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
      for (uint resIdxM = 0; resIdxM < TM; ++resIdxM) {
        for (uint resIdxN = 0; resIdxN < TN; ++resIdxN) {
          threadResults[(wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                        (wSubColIdx * TN) + resIdxN] +=
              regM[wSubRowIdx * TM + resIdxM] *
              regN[wSubColIdx * TN + resIdxN];
        }
      }
    }
  }
}

for (uint dotIdx = 0; dotIdx < BK; ++dotIdx) {  // dotIdx is the outer most loop
  // WM = 64, that's why As is broken into 2x64 parts
  // TM = 8, that's why thread processes 8 rows from As
  // WMITER = 1, that's why only single slice in As (2 in the appendix of the drawing)
  for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
    // load from As into register regM
    for (uint i = 0; i < TM; ++i) {
      regM[wSubRowIdx * TM + i] =
          As[(dotIdx * BM) + warpRow * WM + wSubRowIdx * WSUBM +
              threadRowInWarp * TM + i];
    }
  }
  // WN = 64, that's why Bs is broken into 2x64 parts
  // TN = 4, that's why 4 columns per slice of Bs
  // WNITER = 4, that's why four slices in Bs
  // WSUBN = WN/WNITER = 16 (used to iterate over slices)
  for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
    for (uint i = 0; i < TN; ++i) {
      // load from Bs into register regN
      regN[wSubColIdx * TN + i] =
          Bs[(dotIdx * BN) + warpCol * WN + wSubColIdx * WSUBN +
              threadColInWarp * TN + i];
    }
  }

  // execute warptile matmul via a sum of partial outer products
  for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
    for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
      for (uint resIdxM = 0; resIdxM < TM; ++resIdxM) {
        for (uint resIdxN = 0; resIdxN < TN; ++resIdxN) {
          threadResults[(wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                        (wSubColIdx * TN) + resIdxN] +=
              regM[wSubRowIdx * TM + resIdxM] *
              regN[wSubColIdx * TN + resIdxN];
        }
      }
    }
  }
}

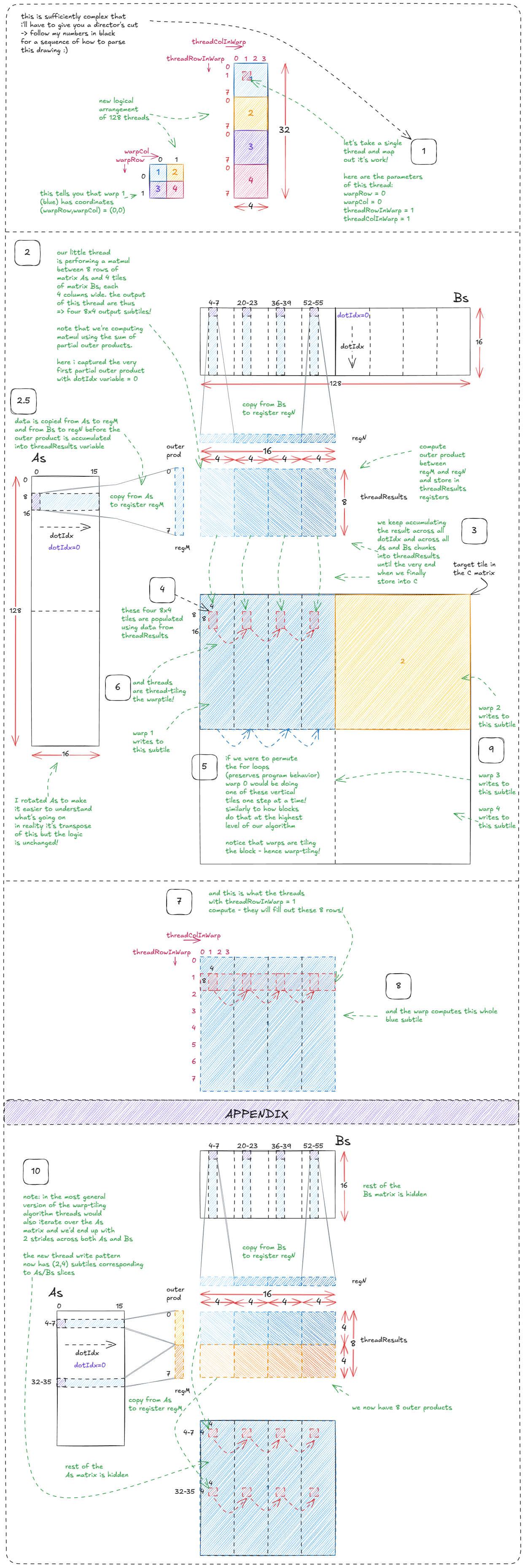
图 33：在 As 和 Bs 之间执行矩阵乘法作为一系列线程级外积（warp-tiling + thread-tiling）。

图 33：在 As 和 Bs 之间执行矩阵乘法作为一系列线程级外积（warp-tiling + thread-tiling）。

一旦块被处理，我们再次同步。这防止了竞争条件——如果没有它，一些线程可能开始将下一个块写入As和Bs，而其他线程仍在处理当前块。

同步后，我们将A和B的指针前进Bk，算法重复直到所有块都被处理。

A += BK;     // move BK columns to right
B += BK * N; // move BK rows down

A += BK;     // move BK columns to right
B += BK * N; // move BK rows down

最后，一旦循环完成，128 个线程将其私有threadResults寄存器刷新到矩阵C的相应输出瓦片中（现在包含完整的点积！）。

在实践中，您会为特定 GPU 自动调整此算法的参数。但如前所述，这种内核风格不再是首选方法——现代 GPU 具有异步内存机制和张量核心（tensor cores），将性能推远超出仅 warp-tiling 所能提供的水平。

接下来，让我们转向 Hopper 上的真正 SOTA（state-of-the-art）。

📝下一章的补充阅读：

我强烈推荐 Pranjal 的优秀博客文章（blog post） [15]，它读起来更像工作日志。在本章中，我将遵循他工作日志中的内核。与 Simon 的工作类似，大部分代码似乎受 CUTLASS 启发（例如，参见这些帖子：CUTLASSping pong kernel [16] 和 efficient GEMM）。

值得注意的是，细节决定成败，Pranjal 成功超越了 cuBLAS SOTA——在几个目标矩阵维度上达到约 107%的 cuBLAS 性能。

在 Hopper 上设计 SOTA 异步矩阵乘法内核¶

现在是时候利用所有硬件特性，在 Hopper 上达到真正 SOTA。我们将使用：

TMA 同步加载/存储操作（TMA sync load/store operations）
张量核心（Tensor Cores）
bf16 精度（bf16 precision）

这些硬件特性既显著简化了 warp-tiling 方法，又将性能提升了近一个数量级——Pranjal 报告从 32 TFLOP/s 增加到 317 TFLOP/s，提升了 10 倍。

📝参考代码：

我将以 kernel 2 [17] 作为这里的参考（另见我的 PR）。注意符号已从 Simon 的略有变化：As→sA和Bs→sB。

这种简化可行的原因是 TMA 和张量核心抽象了我们之前处理的许多手动复杂性。

作为迈向 Hopper SOTA 的第一步，让我们修改 warp-tiling 基线。

我们保持完全相同的程序结构，除了：

我们现在每个线程块只需要 128 个线程（4 个 warps）。
瓦片大小设置为BM = BN = BK = 64。

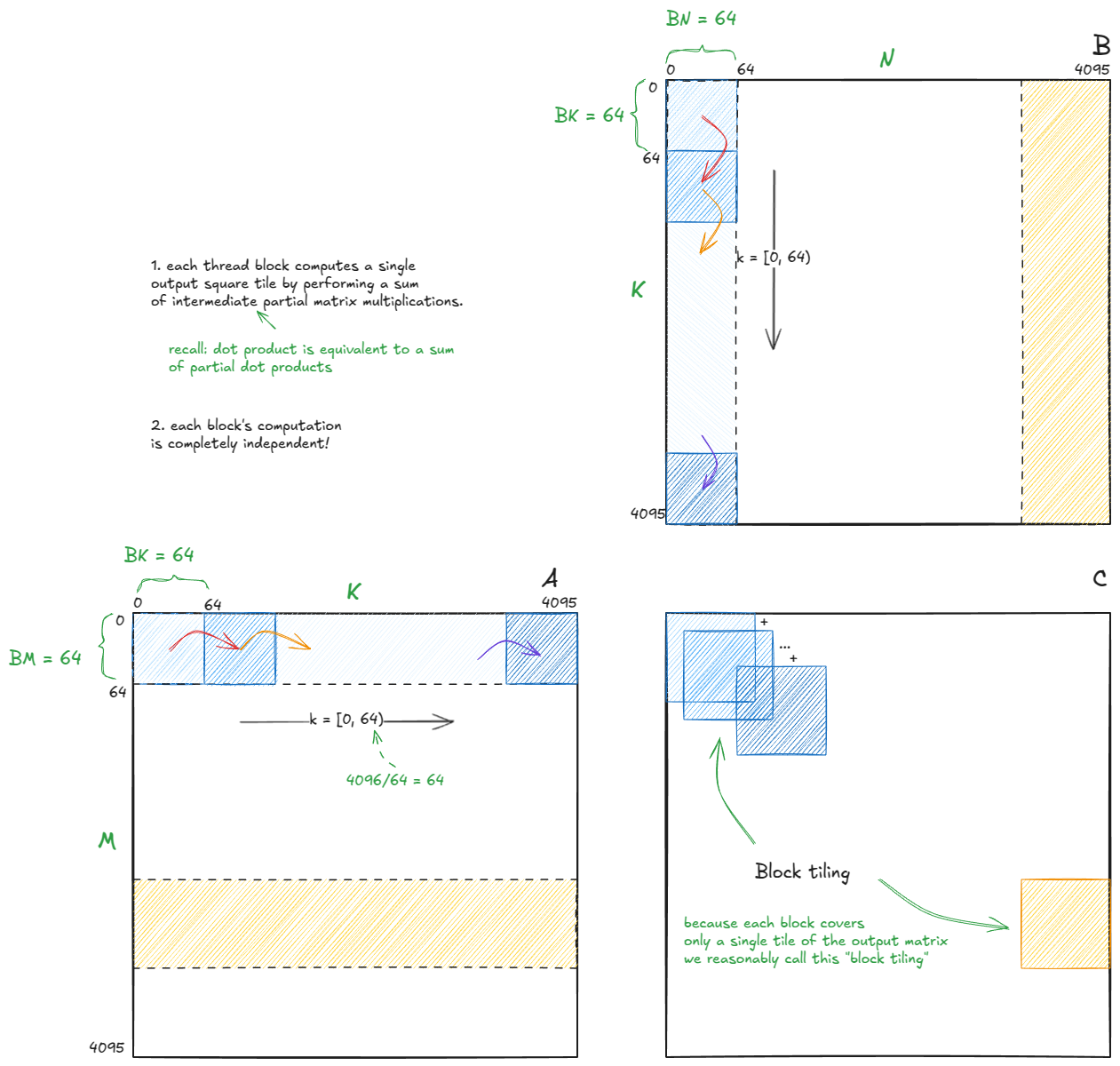
图 34：我们保持 warp-tiling 算法（block-tiling）相同的高级结构。

图 34：我们保持 warp-tiling 算法（block-tiling）相同的高级结构。

💡矩阵格式更改：

重要：A 仍为行主序（row-major），但 B 现在为列主序（column-major）格式。

通过 TMA 异步加载到 SMEM¶

对于第二阶段——将数据加载到 SMEM——TMA 用更简单的东西替换了复杂的 warp 级加载模式。我们只需要：

为A和B构建张量映射（tensor maps）。
触发 TMA 操作（由块中的单个线程完成）。
使用共享内存屏障（shared-memory barriers）同步。

TMA 不仅移动数据，还自动应用 swizzling，这解决了我们之前在 warp-tiling 中看到的存储体冲突（bank conflicts）。（我将在后面的专门部分详细讨论 swizzling。）

要形成张量映射，我们使用cuTensorMapEncodeTiled（参见 docs）。此函数编码了将A和B的块从 GMEM 传输到 SMEM 所需的所有元数据。我们需要每个A和B一个张量映射，但结构上它们相同。对于A，我们指定：

数据类型：bf16
秩：2（矩阵）
指针：A
形状：(K,M)（最快步长维度优先）
行步长：K * sizeof(bf16)
sA的形状：(BK, BM)
Swizzle 模式：加载到sA

时使用 128B 模式

__shared__ barrier barA;  // SMEM barriers for A and B
__shared__ barrier barB;
 
if (threadIdx.x == 0) {
    // initialize with all 128 threads
    init(&barA, blockDim.x);
    init(&barB, blockDim.x);
    // make initialized barrier visible to async proxy
    cde::fence_proxy_async_shared_cta();
}
__syncthreads();  // ensure barriers are visible to all threads

__shared__ barrier barA;  // SMEM barriers for A and B
__shared__ barrier barB;
 
if (threadIdx.x == 0) {
    // initialize with all 128 threads
    init(&barA, blockDim.x);
    init(&barB, blockDim.x);
    // make initialized barrier visible to async proxy
    cde::fence_proxy_async_shared_cta();
}
__syncthreads();  // ensure barriers are visible to all threads

接下来：sA这里我们初始化 SMEM 屏障，用于同步写入sB和

。屏障用所有 128 个线程初始化，因为我们期望块中的每个线程在屏障切换到“就绪”状态前到达。cde::fence_proxy_async_shared_cta()调用

是 Hopper 代理内存模型的一部分。它在 CTA（块）范围内排序“异步代理”（TMA）和“通用代理”（正常线程 ld/st）之间的可见性。这里我们在初始化后立即发出它，以便异步引擎看到屏障的初始化状态。（异步复制的完成将由 mbarrier 本身发出信号。）

完全披露：我也不声称完全理解所有内存一致性细节——官方文档也没有确切帮助。这可能值得单独写一篇后续文章。如果有人有关于此主题的好资源——请联系我！K在外部

for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter) {
    if (threadIdx.x == 0) {  // only one thread launches TMA
        // Offsets into GMEM for this CTA's tile:
        //   A: (block_k_iter * BK, num_block_m * BM)
        cde::cp_async_bulk_tensor_2d_global_to_shared(
            &sA[0], tensorMapA, block_k_iter*BK, num_block_m*BM, barA);
        // update barrier with the number of bytes it has to wait before flipping:
        // sizeof(sA)
        tokenA = cuda::device::barrier_arrive_tx(barA, 1, sizeof(sA));
        //   B: (block_k_iter * BK, num_block_n * BN)
        cde::cp_async_bulk_tensor_2d_global_to_shared(
            &sB[0], tensorMapB, block_k_iter*BK, num_block_n*BN, barB);
        tokenB = cuda::device::barrier_arrive_tx(barB, 1, sizeof(sB));
    } else {
        tokenA = barA.arrive();  // threads-only arrival (no byte tracking)
        tokenB = barB.arrive();
    }
    barA.wait(std::move(tokenA));  // blocks until: all threads arrived AND TMA finished
    barB.wait(std::move(tokenB));

for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter) {
    if (threadIdx.x == 0) {  // only one thread launches TMA
        // Offsets into GMEM for this CTA's tile:
        //   A: (block_k_iter * BK, num_block_m * BM)
        cde::cp_async_bulk_tensor_2d_global_to_shared(
            &sA[0], tensorMapA, block_k_iter*BK, num_block_m*BM, barA);
        // update barrier with the number of bytes it has to wait before flipping:
        // sizeof(sA)
        tokenA = cuda::device::barrier_arrive_tx(barA, 1, sizeof(sA));
        //   B: (block_k_iter * BK, num_block_n * BN)
        cde::cp_async_bulk_tensor_2d_global_to_shared(
            &sB[0], tensorMapB, block_k_iter*BK, num_block_n*BN, barB);
        tokenB = cuda::device::barrier_arrive_tx(barB, 1, sizeof(sB));
    } else {
        tokenA = barA.arrive();  // threads-only arrival (no byte tracking)
        tokenB = barB.arrive();
    }
    barA.wait(std::move(tokenA));  // blocks until: all threads arrived AND TMA finished
    barB.wait(std::move(tokenB));

循环中：A逐步发生了什么（对于B和

）：cp_async_bulk _tensor_2d_global_to_shared(...)线程 0 启动 TMA，使用sA，指定 SMEM 目标（sB/
）、张量映射，以及 GMEM 偏移指定源 GMEM 块。barrier_arrive_tx(bar, 1, sizeof(sX))它立即调用
- ，该函数：
- 计数线程到达数（这里为 1，来自线程 0），并且用预期字节数bar.arrive()武装屏障，以便它知道异步复制何时完成。所有其他线程调用
，贡献它们的到达数（无字节）。bar.wait(token)然后每个线程调用
- 。此等待仅在两个条件都为真时完成：
- 所有 128 个线程都已到达，并且sizeof(sX)异步引擎已将全部

字节写入共享内存。

此加载模式是标准的 Hopper 惯用语——您会在现代内核中到处看到它。在异步复制期间，TMA 还使用128B swizzle 格式

对数据进行了 swizzling。

Swizzling¶

让我们从一个激励性示例开始：

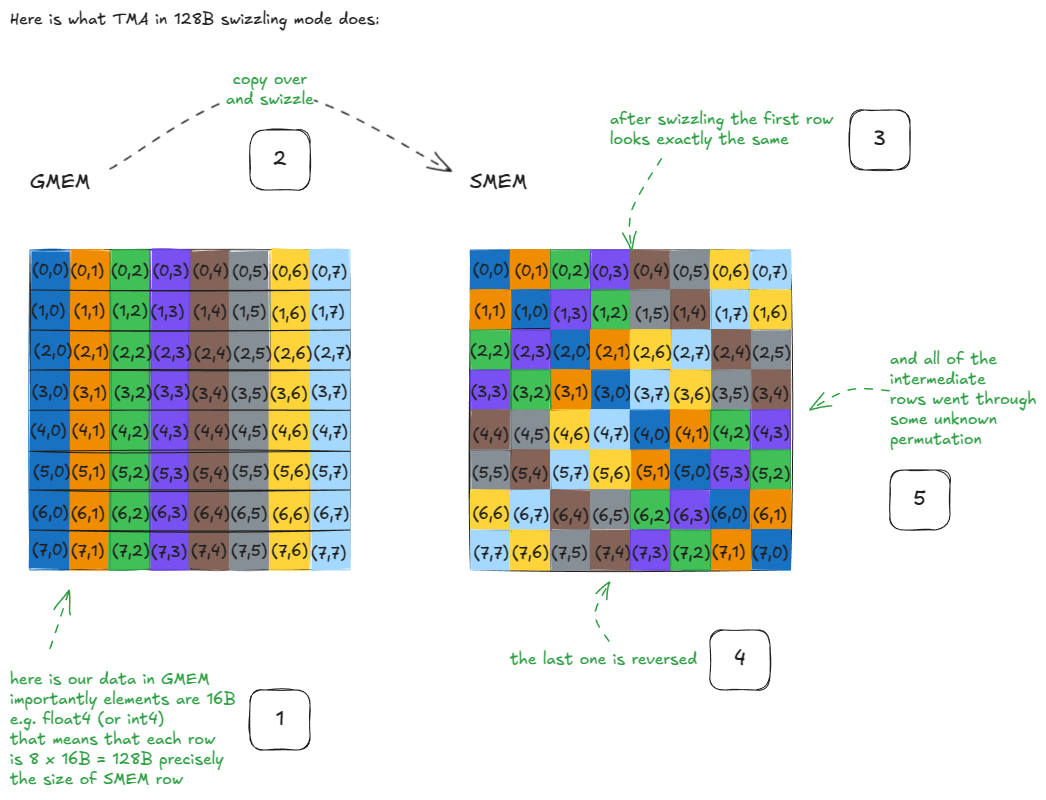
图 35：Swizzling 示例

图 35：Swizzling 示例

这里发生了什么？

假设我们想从原始 GMEM 矩阵的第一行加载所有元素。Swizzling 后，这仍然很简单：只需从 SMEM 矩阵读取第一行。那里没有什么特别的。

现在，假设我们想要原始 GMEM 矩阵的第一列。注意这些元素现在位于 SMEM 的对角线上。这意味着我们可以在单个周期内加载它们，因为没有两个线程访问同一个存储体——零存储体冲突。

如果不进行交织（swizzling），这个访问会将所有列元素映射到同一个存储体但不同地址，产生 8 路存储体冲突，并将吞吐量降低 8 倍。

同样的属性适用于任何行或列：经过交织后，它们都可以在单个周期内被服务！

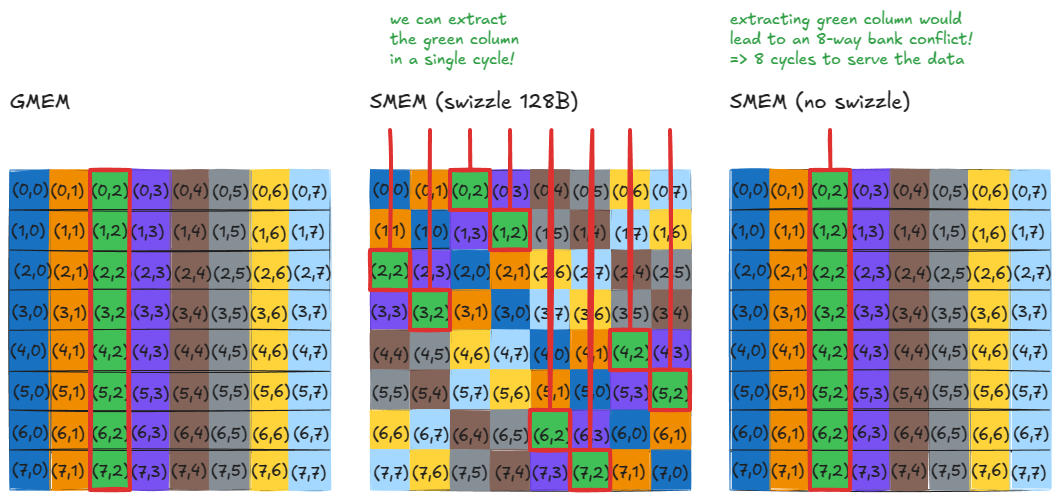
图 36：加载行或列时无存储体冲突

图 36：加载行或列时无存储体冲突

同样的属性适用于存储操作。例如，如果你想在 SMEM 中转置一个矩阵，朴素的方法是：加载一行，然后将其写回为一列。如果不进行交织，这会导致 8 路存储体冲突。

启用交织后，我们避免了这个问题，但你必须小心索引。

📝注意

TMA 在将数据从 SMEM 移回 GMEM 时会自动取消交织（unswizzles）。

既然动机已经清楚，让我们提出以下问题：TMA 实际上如何生成交织模式？

事实证明答案很简单：与特定掩码模式进行 XOR 运算。

快速回顾 XOR，这是真值表：

0, 0 映射到 0
0, 1 映射到 1
1, 0 映射到 1
1, 1 映射到 0

值得注意的是：当其中一个位为 1 时，XOR 会翻转另一个位。

通常，我们可以在 CUTLASS 中找到答案。另一位 Simon（不是之前那位）也很好地解释了掩码模式是如何生成 [18] 的——尽管没有完全说明该模式如何导致我们刚刚看到的特定交织布局。

因此，两个大问题仍然存在：

XOR 掩码是如何生成的？
掩码实际上如何应用以产生交织模式？

生成 XOR 掩码¶

NVIDIA 将每个交织模式与特定的“交织函数”关联：

128B 交织模式与Swizzle<3,4,3>
64B 交织模式与Swizzle<2,4,3>
32B 交织模式与Swizzle<1,4,3>

让我们解析Swizzle<3,4,3>。然后我将分享其他模式的 XOR 掩码。

// To improve readability, I'll group bits in 8s with underscores.

// Swizzle<3, 4, 3>
// -> BBits = 3
// -> MBase = 4
// -> SShift = 3

// Given the decoded arguments from above here are the steps that the swizzling function does:

// Step 1. Compute bit_msk = (1 << BBits) - 1
bit_msk = (0b00000000_00000001 << 3) - 1 = 0b00000000_00000111  // keep 16 bit resolution

// Step 2. Compute yyy_msk = bit_msk << (MBase + max(0, SShift))
yyy_msk = 0b00000000_00000111 << 7 = 0b00000011_10000000

// Step 3. Mask the input number (annotated bits A-P for clarity)
input_number = 0bABCDEFGH_IJKLMNOP

masked = input_number & yyy_mask
  = 0bABCDEFGH_IJKLMNOP & 0b00000011_10000000 = 0b000000GH_I0000000

// Step 4. Shift right by SShift (masked >> SShift)
shifted = masked >> 3
  = 0b000000GH_I0000000 >> 3 = 0b00000000_0GHI0000

// Step 5. XOR with the original input
output = input_number ^ shifted
  = 0bABCDEFGH_IJKLMNOP ^ 0b00000000_0GHI0000 = 0bABCDEFGH_IwyzMNOP

// Replace unchanged bits with x for legibility.
// I'll also uppercase "wyz" to make it stand out and keep GHI around as they have an impact on wyz:
output = 0bxxxxxxGH_IWYZxxxx

// where WYZ = GHI ^ JKL (XOR)

// To improve readability, I'll group bits in 8s with underscores.

// Swizzle<3, 4, 3>
// -> BBits = 3
// -> MBase = 4
// -> SShift = 3

// Given the decoded arguments from above here are the steps that the swizzling function does:

// Step 1. Compute bit_msk = (1 << BBits) - 1
bit_msk = (0b00000000_00000001 << 3) - 1 = 0b00000000_00000111  // keep 16 bit resolution

// Step 2. Compute yyy_msk = bit_msk << (MBase + max(0, SShift))
yyy_msk = 0b00000000_00000111 << 7 = 0b00000011_10000000

// Step 3. Mask the input number (annotated bits A-P for clarity)
input_number = 0bABCDEFGH_IJKLMNOP

masked = input_number & yyy_mask
  = 0bABCDEFGH_IJKLMNOP & 0b00000011_10000000 = 0b000000GH_I0000000

// Step 4. Shift right by SShift (masked >> SShift)
shifted = masked >> 3
  = 0b000000GH_I0000000 >> 3 = 0b00000000_0GHI0000

// Step 5. XOR with the original input
output = input_number ^ shifted
  = 0bABCDEFGH_IJKLMNOP ^ 0b00000000_0GHI0000 = 0bABCDEFGH_IwyzMNOP

// Replace unchanged bits with x for legibility.
// I'll also uppercase "wyz" to make it stand out and keep GHI around as they have an impact on wyz:
output = 0bxxxxxxGH_IWYZxxxx

// where WYZ = GHI ^ JKL (XOR)

用简单语言描述：交织函数查看位GHI（位置 9、8、7，零索引）。如果其中任何一位为 1，它会翻转相应的位JKL（位置 6、5、4）以得到WYZ。所有其他位保持不变。

让我们建立一些关于交织函数行为的直觉：

图 37：交织函数直觉

图 37：交织函数直觉

对于 32B 和 64B 交织模式，交织函数是0bxxxxxxxx_IxxZxxxx和0bxxxxxxxH_IxYZxxxx。

这些遵循相同的 XOR-with-mask 思想，只是使用不同的控制位来驱动哪些低位被翻转。

这一切如何与我们开始的动机示例联系起来？

这是链接：

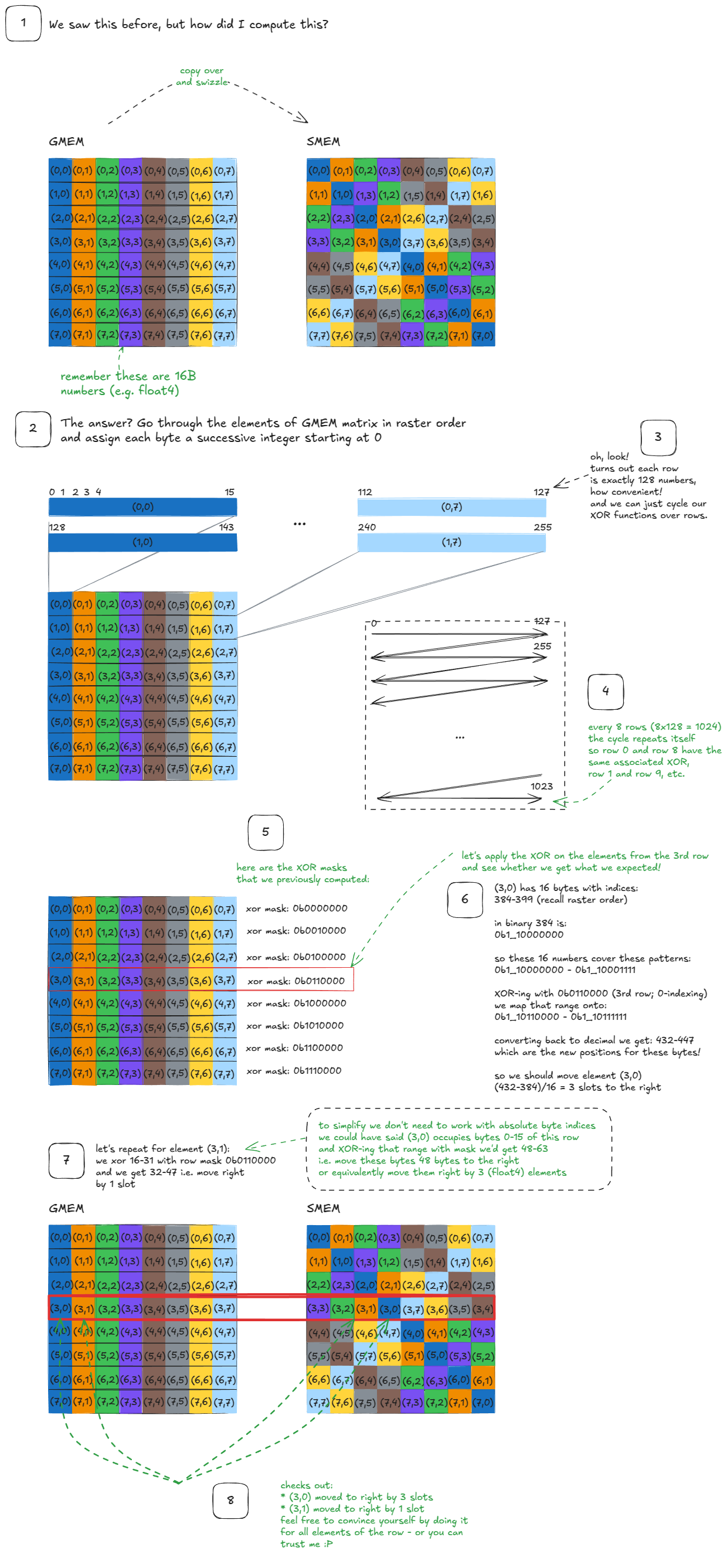
图 38：将交织函数连接到矩阵交织示例

图 38：将交织函数连接到矩阵交织示例

这就是交织的 WHY 和 HOW。 :)

Tensor Cores¶

回到张量核心（Tensor Cores）。此时，我们已经将A和B的块从 GMEM 拉入 SMEM 中的sA和sB。它们已经交织，并准备好供张量核心使用。

NVIDIA 公开了几种矩阵乘加（MMA）指令：

wmma——warp 协作、同步（旧世代）。
mma.sync——warp 协作、同步（Ampere）。
wgmma.mma_async——warp 组协作、异步（Hopper）。

📝注意：

一个warp 组 = 4 个 warps = CUDA 中的 128 个线程。

我们将专注于wgmma.mma_async（文档 [19]），因为它随 Hopper 引入，是目前最强大的。它是异步的，并利用 4 个协作的 warps 一起计算矩阵乘法；这正是我们选择块大小=128 的原因。

对于 bf16 操作数，wgmma支持形状为m64nNk16的形式，其中N ∈ {8, 16, 24, …, 256}。在我们当前的示例中，我们将使用m64n64k16，但一般来说，更大的N值性能更高（只要你有足够的寄存器和 SMEM 来支持它们）。

📝注意：

m64n64k16意味着张量核心一次性计算一个64×16 × 16×64的矩阵乘法。

以下是操作数放置规则：sA可以驻留在寄存器或 SMEM 中，sB必须驻留在 SMEM 中，而累加器（BM x BN）始终在寄存器中。

由于这对单个线程来说寄存器太多，累加器在 warp 组的线程之间分区。

在我们的参考内核中，你会看到它像这样初始化：

float d[WGMMA_N/16][8];  // d is the accumulator; GEMM: D = A @ B + D
memset(d, 0, sizeof(d));  // init to all 0s

float d[WGMMA_N/16][8];  // d is the accumulator; GEMM: D = A @ B + D
memset(d, 0, sizeof(d));  // init to all 0s

我们设置WGMMA_M = WGMMA_N = BM = BN = 64。这给出：

warp 组中的 128 个线程
每个线程持有WGMMA_N/16 × 8个寄存器
总计：128 × (64/16) × 8 = 64 × 64 个寄存器

…这正好匹配累加器大小（BM × BN = 64 × 64），只是在组中分布。

这是我们将分解的相应张量核心代码片段：

asm volatile("wgmma.fence.sync.aligned;" ::: "memory");
wgmma64<1, 1, 1, 0, 0>(d, &sA[0], &sB[0]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[WGMMA_K], &sB[WGMMA_K]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[2*WGMMA_K], &sB[2*WGMMA_K]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[3*WGMMA_K], &sB[3*WGMMA_K]);
asm volatile("wgmma.commit_group.sync.aligned;" ::: "memory");
asm volatile("wgmma.wait_group.sync.aligned %0;" ::"n"(0) : "memory");

asm volatile("wgmma.fence.sync.aligned;" ::: "memory");
wgmma64<1, 1, 1, 0, 0>(d, &sA[0], &sB[0]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[WGMMA_K], &sB[WGMMA_K]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[2*WGMMA_K], &sB[2*WGMMA_K]);
wgmma64<1, 1, 1, 0, 0>(d, &sA[3*WGMMA_K], &sB[3*WGMMA_K]);
asm volatile("wgmma.commit_group.sync.aligned;" ::: "memory");
asm volatile("wgmma.wait_group.sync.aligned %0;" ::"n"(0) : "memory");

📝注意：

一些 Hopper 指令在 CUDA C++中未公开，因此我们使用asm(...);进入内联 PTX。
::: "memory"是一个内存破坏器，它防止 asm 语句周围的任何内存优化，它是给编译器的“不要将周围的内存访问移过此点”的提示；禁止编译器围绕此语句重新排列内存操作。
volatile告诉编译器 asm 块*必须不*被删除或提升，即使它看起来冗余（参见文档）[20]。

让我们首先解析围绕实际矩阵乘法调用的边界指令（wgmma.fence、commit_group、wait_group）。

wgmma.fence.sync.aligned;——文档解释得很好：“wgmma.fence 在先前对任何 warpgroup 寄存器的访问与后续由 wgmma.mma_async 指令对相同寄存器的访问之间建立顺序。”

在实践中，warp 组的所有四个 warps 必须在第一个wgmma.mma_async之前执行此 fence。

之后，我们就可以开始了。即使累加器寄存器在那些四个 wgmma 调用中被更新，我们之间不需要更多的 fences——对于相同形状并累加到相同寄存器的连续 MMAs 有一个特殊例外。这正是我们这里的情况。

这真的只是样板代码。事实上，如果你注释掉它，编译器会悄悄地为你重新插入。

wgmma.commit_group——另一个样板操作：来自文档的“将所有先前未提交的 wgmma.mma_async 操作提交到一个 wgmma-group”。它关闭了我们刚刚启动的所有wgmma.mma_async（上面的四个调用）到一个单一的“组”中。

wgmma.wait_group 0 - 含义：在此点之前的所有组完成之前不要继续。由于我们只启动了一个组，这里只是说“等待那四个 MMA 完成且结果实际驻留在累加器寄存器中”。

所以标准节奏是：fence → 启动一批异步 MMA → 提交它们 → 等待它们完成。

现在转到 wgmma 本身。wgmma64函数是内联 PTX 调用的包装器：

wgmma.mma_async.sync.aligned.m64n64k16.f32.bf16.bf16

wgmma.mma_async.sync.aligned.m64n64k16.f32.bf16.bf16

操作码的结构使其含义相当透明：f32 是累加器数据类型，bf16 是输入矩阵的数据类型。sA和sB矩阵。

语义是通常的融合乘加：D = A @ B+D即，GEMM 累加到现有的 fp32 瓦片中。（有一个标志可以将其转换为D=A @ B，我们稍后会使用它。）

我故意跳过如何形成和传递sA和sB的 SMEM 描述符的细节。这些描述符编码 SMEM 基地址、交换模式（在我们的情况下为 128B），以及LBO/SBO（前导/步长维度字节偏移）值，以便张量核心能正确导航布局。在此覆盖描述符构造会偏离本已冗长的帖子；它可能值得单独写一篇专注的文章。只需知道存在这个额外的元数据层，其解释我暂时省略了。

这里解释了为什么我们需要 4 次 wgmma 调用：

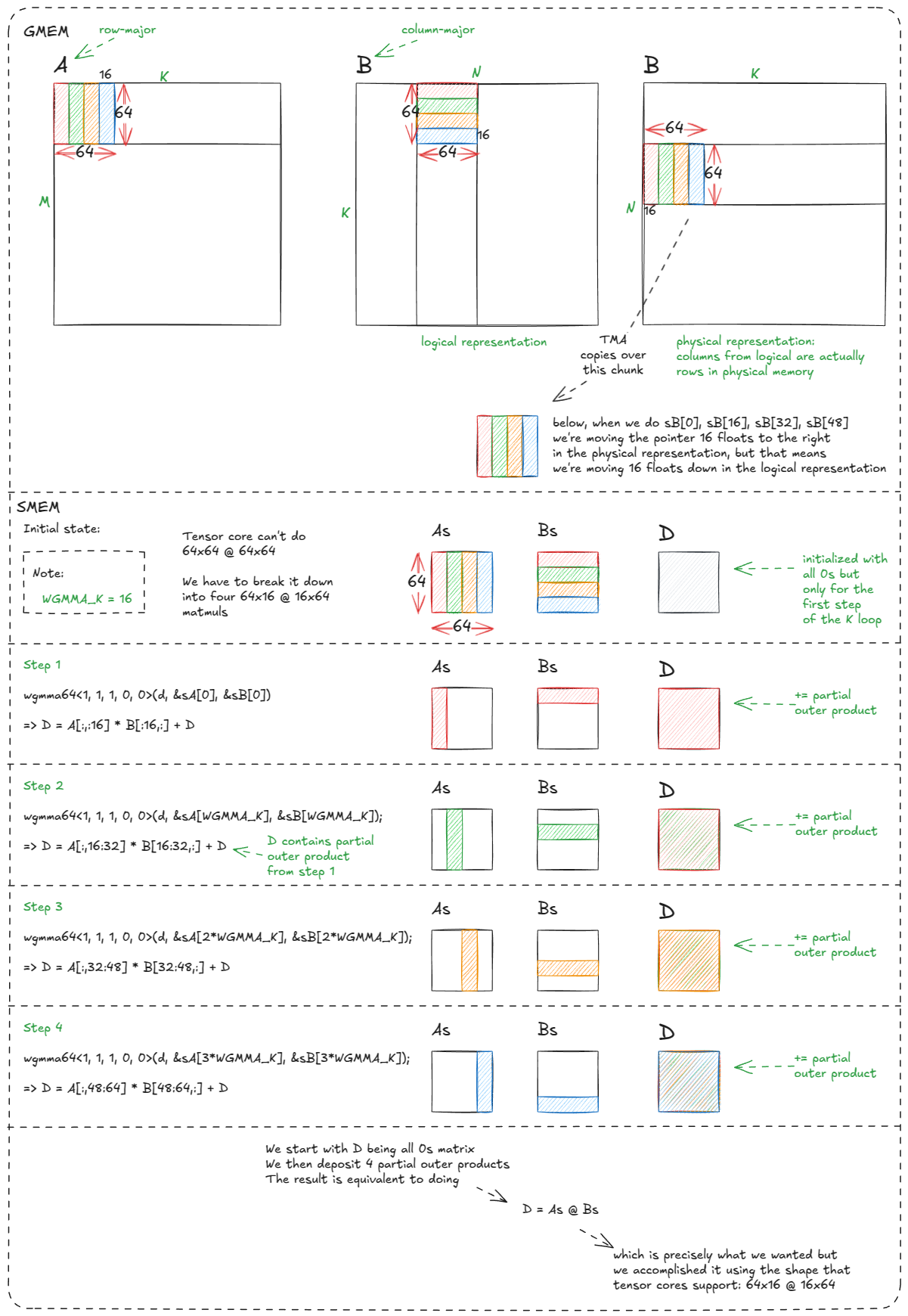
图 39：为什么进行四次 64x16 @ 16x64 wgmma 调用等同于进行 64x64 @ 64x64 矩阵乘法

图 39：为什么进行四次 64x16 @ 16x64 wgmma 调用等同于进行 64x64 @ 64x64 矩阵乘法

这里稍微令人费解的部分是列主表示：如何sB[0] … sB[48]最终映射到正确的逻辑位置/切片。

但关键要点是，我们之前处理的许多 warp-tiling 和 thread-tiling 复杂性现在在硬件中被抽象化了。过去需要跨 warp 精心编排的内容已简化为少量样板指令和一些声明性的 wgmma 调用。

尽管如此，这只是起点。我们仍在浪费 TMA 和张量核心周期：

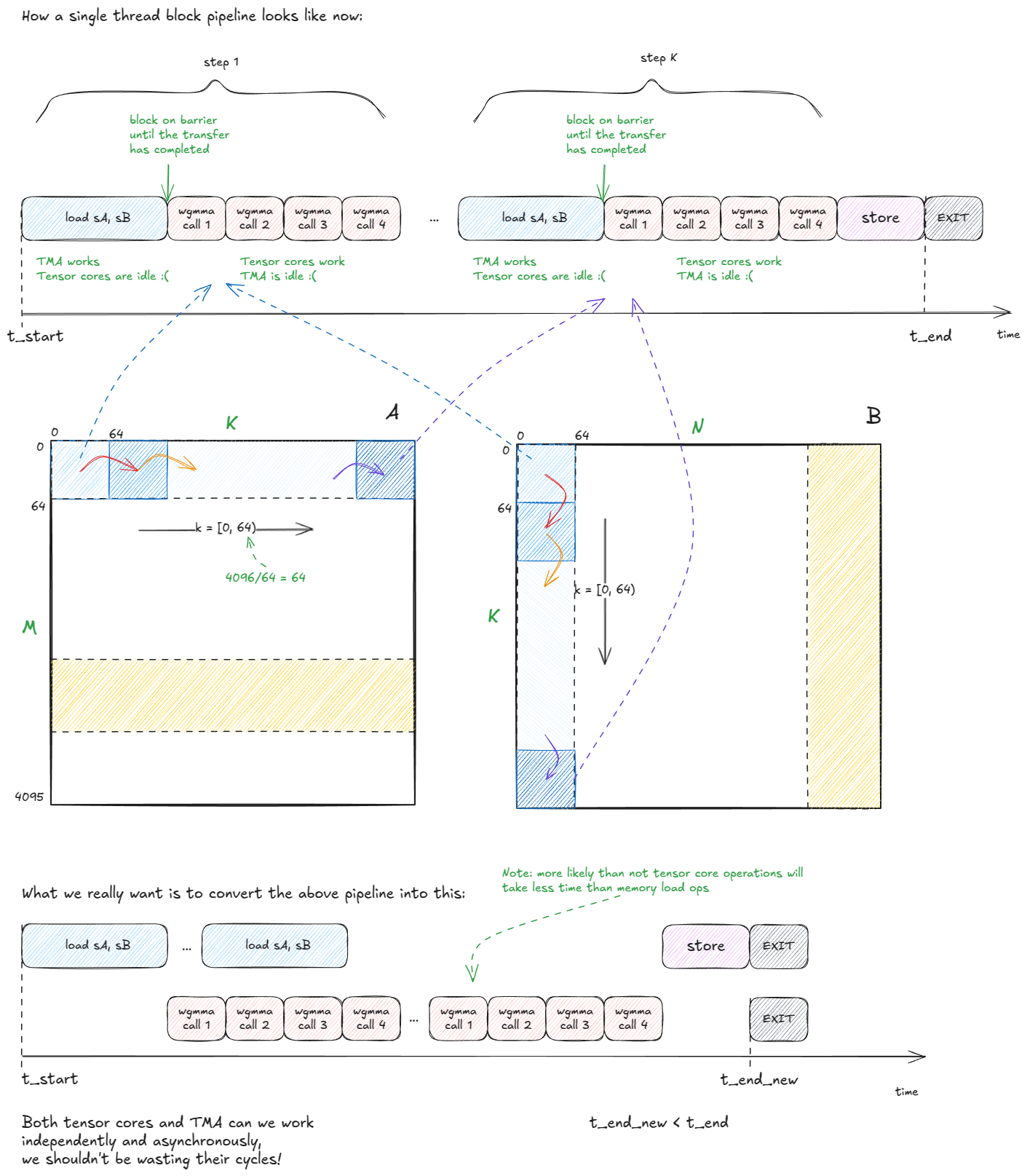
图 40：我们正在浪费 TMA 和 TC 周期 - 我们可以做得更好

图 40：我们正在浪费 TMA 和 TC 周期 - 我们可以做得更好

我们解决浪费周期的方法是通过流水线化计算和数据移动。具体来说，我们将sA和sB（驻留在 SMEM 中的瓦片）转换为一个块队列——比如长度为 5。

然后我们将工作拆分到两个 warp-group：

一个 warp-group 充当producer，负责通过将新的A和B块流式传输到队列中来保持 TMA 忙碌。
另一个 warp-group 充当consumer，从队列中提取以保持张量核心饱和。

自然，这需要协调。我们使用的机制是一个 SMEM 屏障队列，每个队列槽有一个full[i]/empty[i]对来同步生产者和消费者。

参考：kernel 4 代码。

这是设置：

// queue of barriers
__shared__ barrier full[QSIZE], empty[QSIZE];
// use the largest MMA shape available
constexpr int WGMMA_M = 64, WGMMA_K = 16, WGMMA_N=BN;

// queue of barriers
__shared__ barrier full[QSIZE], empty[QSIZE];
// use the largest MMA shape available
constexpr int WGMMA_M = 64, WGMMA_K = 16, WGMMA_N=BN;

初始化与之前类似：

if (threadIdx.x == 0) {
  for (int i = 0; i < QSIZE; ++i) {
      // num_consumers == 1 in this example;
      // 128 threads from consumer wg + 1 producer thread
      init(&full[i], num_consumers * 128 + 1);
      init(&empty[i], num_consumers * 128 + 1);
  }
  cde::fence_proxy_async_shared_cta();  // same as before
}
__syncthreads();  // same as before

if (threadIdx.x == 0) {
  for (int i = 0; i < QSIZE; ++i) {
      // num_consumers == 1 in this example;
      // 128 threads from consumer wg + 1 producer thread
      init(&full[i], num_consumers * 128 + 1);
      init(&empty[i], num_consumers * 128 + 1);
  }
  cde::fence_proxy_async_shared_cta();  // same as before
}
__syncthreads();  // same as before

需要注意两点：

我们已升级到更大的张量核心 MMA（从m64n64k16到m64nBNk16），因为经验上它有助于最大化计算吞吐量。
由于队列是多槽的，屏障初始化必须循环所有条目。

这是主要逻辑：

在生产者（wg_idx = 0）中，一个线程协调 TMA 复制到队列。它使用empty[qidx].wait()来阻塞直到缓冲区槽空闲，然后为cp_async_bulk_tensor _2d_global_to_shared和sA发出sB。最后，它用barrier_arrive_tx发出完成信号，将屏障与复制的字节数绑定。
在消费者（wg_idx > 0）中，所有线程首先将每个队列槽标记为“空”（准备填充）。然后，对于每个K步骤，它们等待full[qidx]，在该缓冲区上运行张量核心 MMA，完成后再次将槽标记为空。

// Producer
if (wg_idx == 0) {  // wg_idx = threadIdx.x / 128
    if (tid == 0) {  // only thread 0 issues TMA calls
        int qidx = 0;  // index into the circular buffer
        for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter, ++qidx) {
            if (qidx == QSIZE) qidx = 0;  // wrap around
            // wait until this buffer is marked empty (ready to be written into)
            empty[qidx].wait(empty[qidx].arrive());
            // copy over chunks from A and B
            cde::cp_async_bulk_tensor_2d_global_to_shared(
                &sA[qidx*BK*BM], tensorMapA, block_k_iter*BK, num_block_m*BM, full[qidx]);
            cde::cp_async_bulk_tensor_2d_global_to_shared(
                &sB[qidx*BK*BN], tensorMapB, block_k_iter*BK, num_block_n*BN, full[qidx]);
            // mark barrier with the expected byte count (non-blocking)
            barrier::arrival_token _ = cuda::device::barrier_arrive_tx(
              full[qidx], 1, (BK*BN+BK*BM)*sizeof(bf16));
        }
    }
} else {
    // Consumer warp-group
    for (int i = 0; i < QSIZE; ++i) {
        // i initially, all buffers are considered empty; ready for write
        // all 128 consumer threads arrive on each barrier
        barrier::arrival_token _ = empty[i].arrive();
    }
    // distributed accumulator registers, zero-initialized
    float d[BM/WGMMA_M][WGMMA_N/16][8];
    memset(d, 0, sizeof(d));
 
    int qidx = 0;
    for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter, ++qidx) {
        if (qidx == QSIZE) qidx = 0;  // wrap around
        // wait until TMA has finished filling this buffer
        full[qidx].wait(full[qidx].arrive());
 
        // core tensor core loop
        warpgroup_arrive();  // convenience wrapper around the PTX boilerplate
        #pragma unroll  // compiler hint (we saw this in PTX/SASS section)
        // submit as many tensor core ops as needed to compute sA @ sB (see drawing)
        for (int m_it = 0; m_it < BM/WGMMA_M; ++m_it) {
            bf16 *wgmma_sA = sA + qidx*BK*BM + BK*m_it*WGMMA_M;
            #pragma unroll
            for (int k_it = 0; k_it < BK/WGMMA_K; ++k_it) {
                wgmma<WGMMA_N, 1, 1, 1, 0, 0>(
                  d[m_it], &wgmma_sA[k_it*WGMMA_K], &sB[qidx*BK*BN + k_it*WGMMA_K]);
            }
        }
        warpgroup_commit_batch();
        warpgroup_wait<0>();
 
        // all 128 consumer threads mark buffer as consumed so producer can reuse it
        barrier::arrival_token _ = empty[qidx].arrive();
    }
 
    // finally: write accumulator d back to output matrix C
 
}

// Producer
if (wg_idx == 0) {  // wg_idx = threadIdx.x / 128
    if (tid == 0) {  // only thread 0 issues TMA calls
        int qidx = 0;  // index into the circular buffer
        for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter, ++qidx) {
            if (qidx == QSIZE) qidx = 0;  // wrap around
            // wait until this buffer is marked empty (ready to be written into)
            empty[qidx].wait(empty[qidx].arrive());
            // copy over chunks from A and B
            cde::cp_async_bulk_tensor_2d_global_to_shared(
                &sA[qidx*BK*BM], tensorMapA, block_k_iter*BK, num_block_m*BM, full[qidx]);
            cde::cp_async_bulk_tensor_2d_global_to_shared(
                &sB[qidx*BK*BN], tensorMapB, block_k_iter*BK, num_block_n*BN, full[qidx]);
            // mark barrier with the expected byte count (non-blocking)
            barrier::arrival_token _ = cuda::device::barrier_arrive_tx(
              full[qidx], 1, (BK*BN+BK*BM)*sizeof(bf16));
        }
    }
} else {
    // Consumer warp-group
    for (int i = 0; i < QSIZE; ++i) {
        // i initially, all buffers are considered empty; ready for write
        // all 128 consumer threads arrive on each barrier
        barrier::arrival_token _ = empty[i].arrive();
    }
    // distributed accumulator registers, zero-initialized
    float d[BM/WGMMA_M][WGMMA_N/16][8];
    memset(d, 0, sizeof(d));
 
    int qidx = 0;
    for (int block_k_iter = 0; block_k_iter < num_blocks_k; ++block_k_iter, ++qidx) {
        if (qidx == QSIZE) qidx = 0;  // wrap around
        // wait until TMA has finished filling this buffer
        full[qidx].wait(full[qidx].arrive());
 
        // core tensor core loop
        warpgroup_arrive();  // convenience wrapper around the PTX boilerplate
        #pragma unroll  // compiler hint (we saw this in PTX/SASS section)
        // submit as many tensor core ops as needed to compute sA @ sB (see drawing)
        for (int m_it = 0; m_it < BM/WGMMA_M; ++m_it) {
            bf16 *wgmma_sA = sA + qidx*BK*BM + BK*m_it*WGMMA_M;
            #pragma unroll
            for (int k_it = 0; k_it < BK/WGMMA_K; ++k_it) {
                wgmma<WGMMA_N, 1, 1, 1, 0, 0>(
                  d[m_it], &wgmma_sA[k_it*WGMMA_K], &sB[qidx*BK*BN + k_it*WGMMA_K]);
            }
        }
        warpgroup_commit_batch();
        warpgroup_wait<0>();
 
        // all 128 consumer threads mark buffer as consumed so producer can reuse it
        barrier::arrival_token _ = empty[qidx].arrive();
    }
 
    // finally: write accumulator d back to output matrix C
 
}

可视化应该使其更清晰：

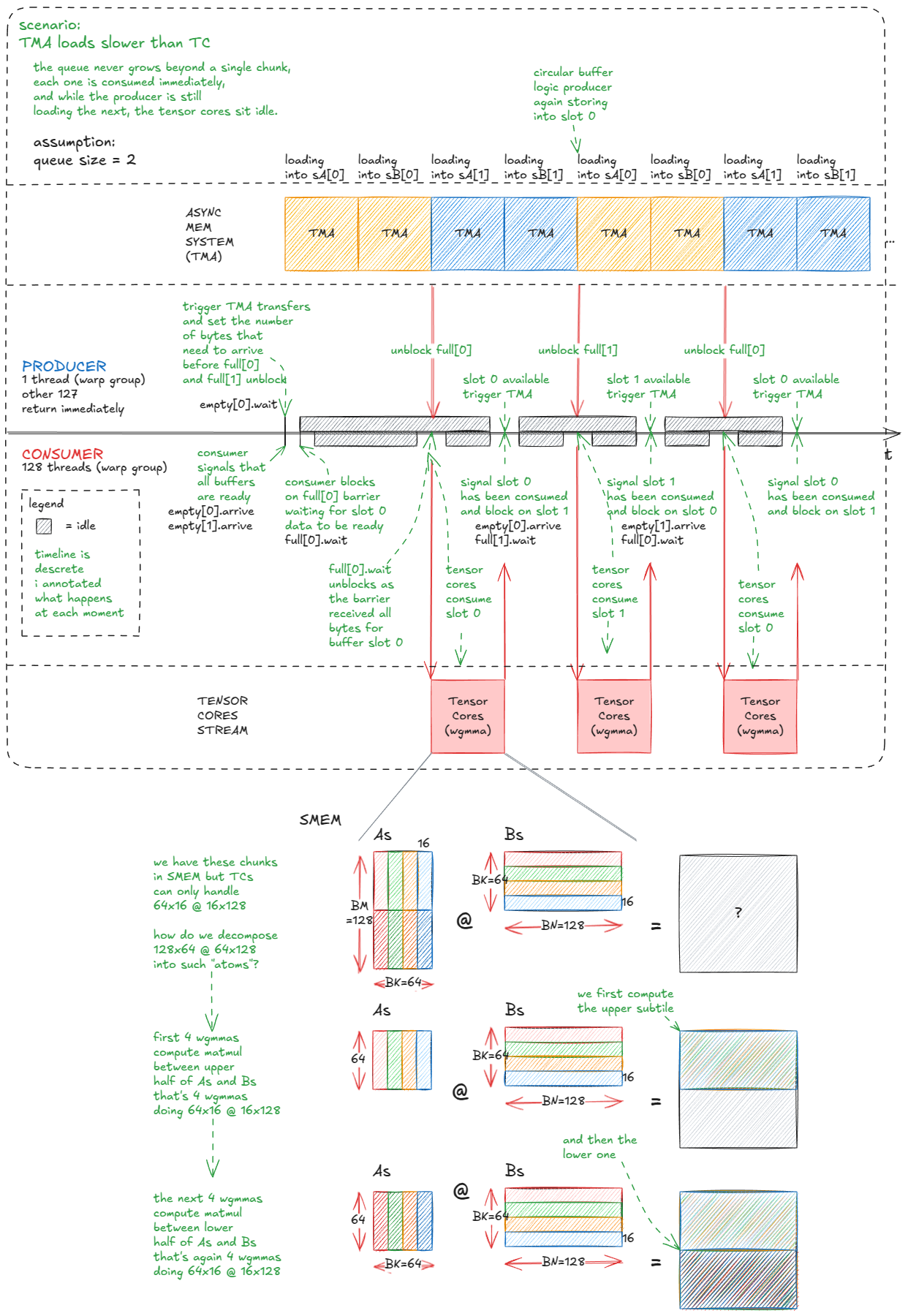
图 41：更高效的 TC/TMA 流水线：生产者 warp-group 将瓦片流式传输到循环缓冲区；消费者 warp-group 将瓦片排入张量核心。

一个自然的调整是将输出瓦片从 128×128 增长到 128×256。问题在于，在该大小下，单个消费者 warp-group 中每个线程的累加器分片变得太大——每个线程需要 256 个 fp32 寄存器仅用于累加器，这超出了每个线程的寄存器预算（并触发寄存器溢出到设备内存——这对性能非常不利）。

修复方法是添加另一个消费者 warp-group，以便累加器在两个组之间分片而不是一个。我们保持单个生产者（以驱动 TMA）并启动块/CTA 使用 3×128 = 384 个线程：

WG0：生产者（TMA）
WG1：消费者 A（计算 128×256 瓦片的上半部分）
WG2：消费者 B（计算下半部分）

每个消费者拥有输出的 64×256 半瓦片，因此每个线程的累加器占用减半，避免溢出。

这是现在如何执行矩阵乘法的：

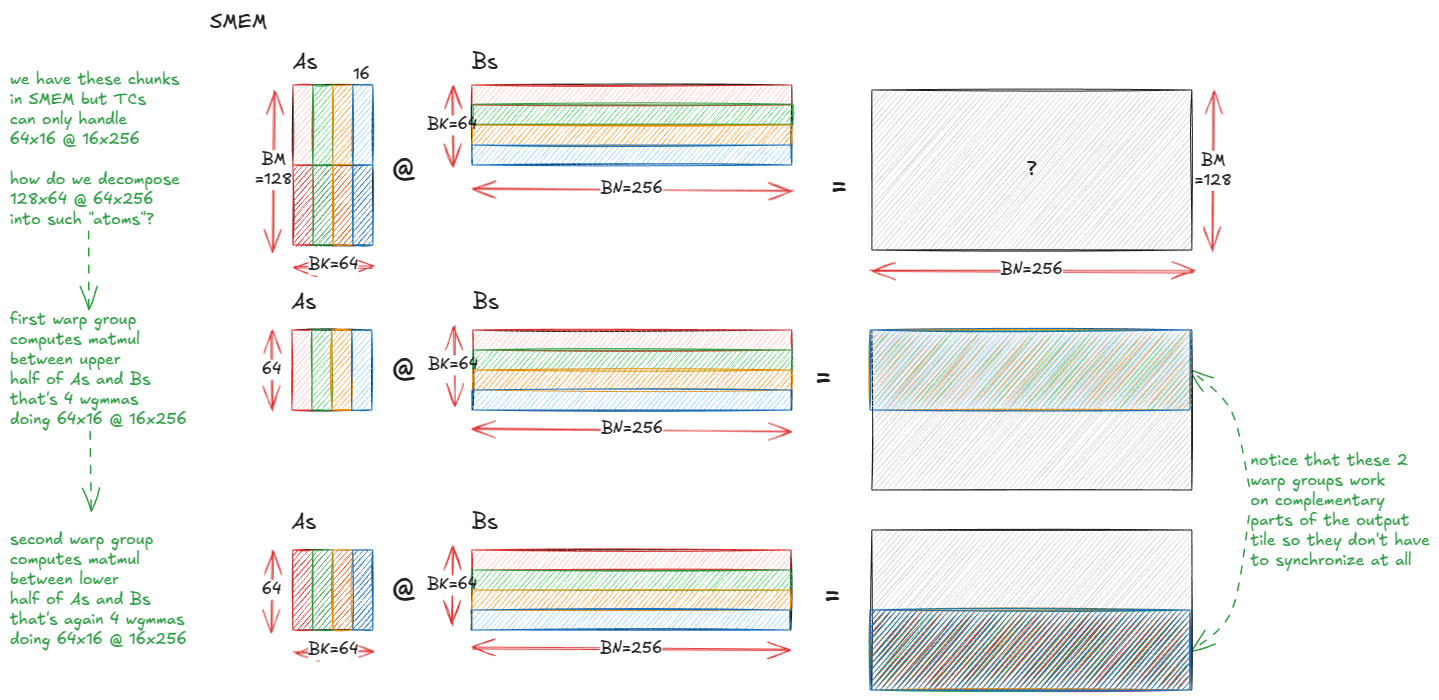
图 42：两个消费者 warp group 让我们可以将瓦片从 128x128 -> 128x256 增长而无需寄存器溢出

图 42：两个消费者 warp group 让我们可以将瓦片从 128x128 -> 128x256 增长而无需寄存器溢出

下一个大想法是，我们也可以隐藏写入输出瓦片的延迟：

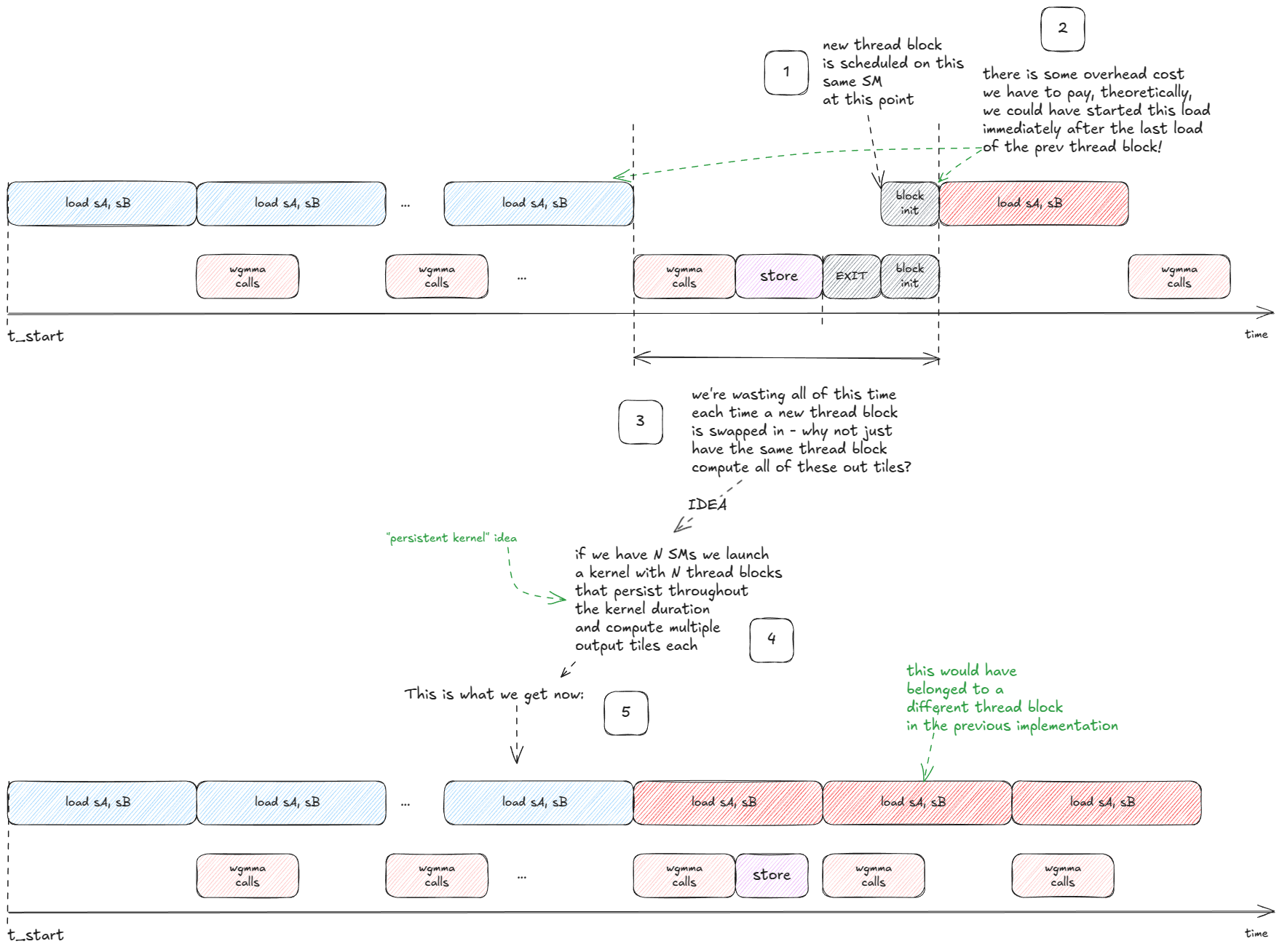
图 43：持久化内核：通过启动每个 SM 一个长存活的块来处理许多瓦片，将输出存储与传入加载重叠。

💡持久化内核

持久化内核启动少量固定数量的线程块（通常每个 SM 一个）并保持它们在整个工作负载期间存活。每个块运行一个内部循环，从队列中拉取新瓦片直到工作完成，而不是为每个瓦片启动一个块。

这引发了一个自然问题：每个 SM 应该处理哪个输出瓦片子集，以及以什么顺序？

这个调度策略看起来如何？

让我们从一个玩具设置开始来推理选项：

输出瓦片总数：64。
SM 数量：10。
所以每个 SM 平均必须处理约 6.4 个块。

第一次尝试可能看起来像这样：

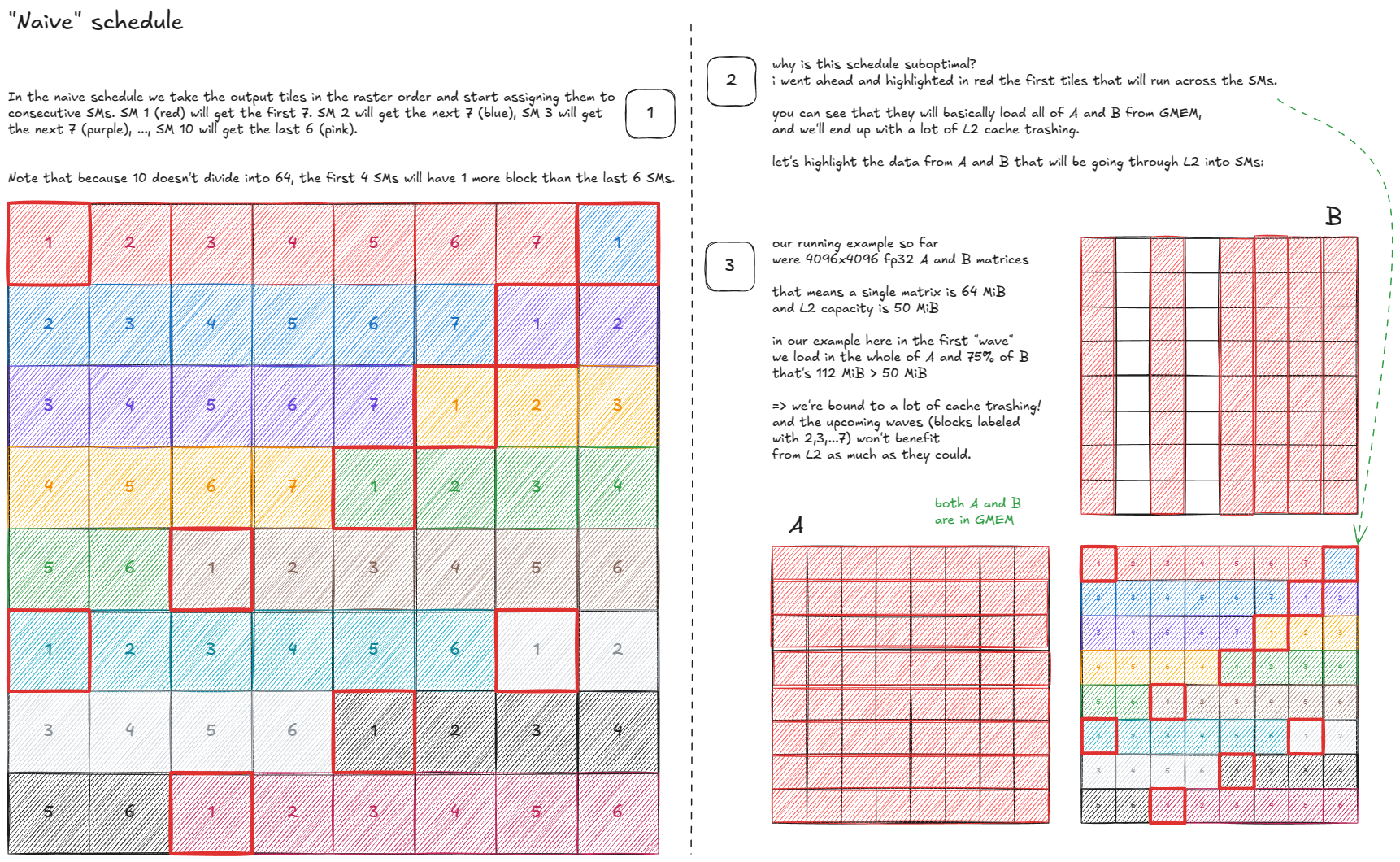
图 44：朴素调度

图 44：朴素调度

我们能做得更好吗？是的——通过使调度具有缓存感知性：

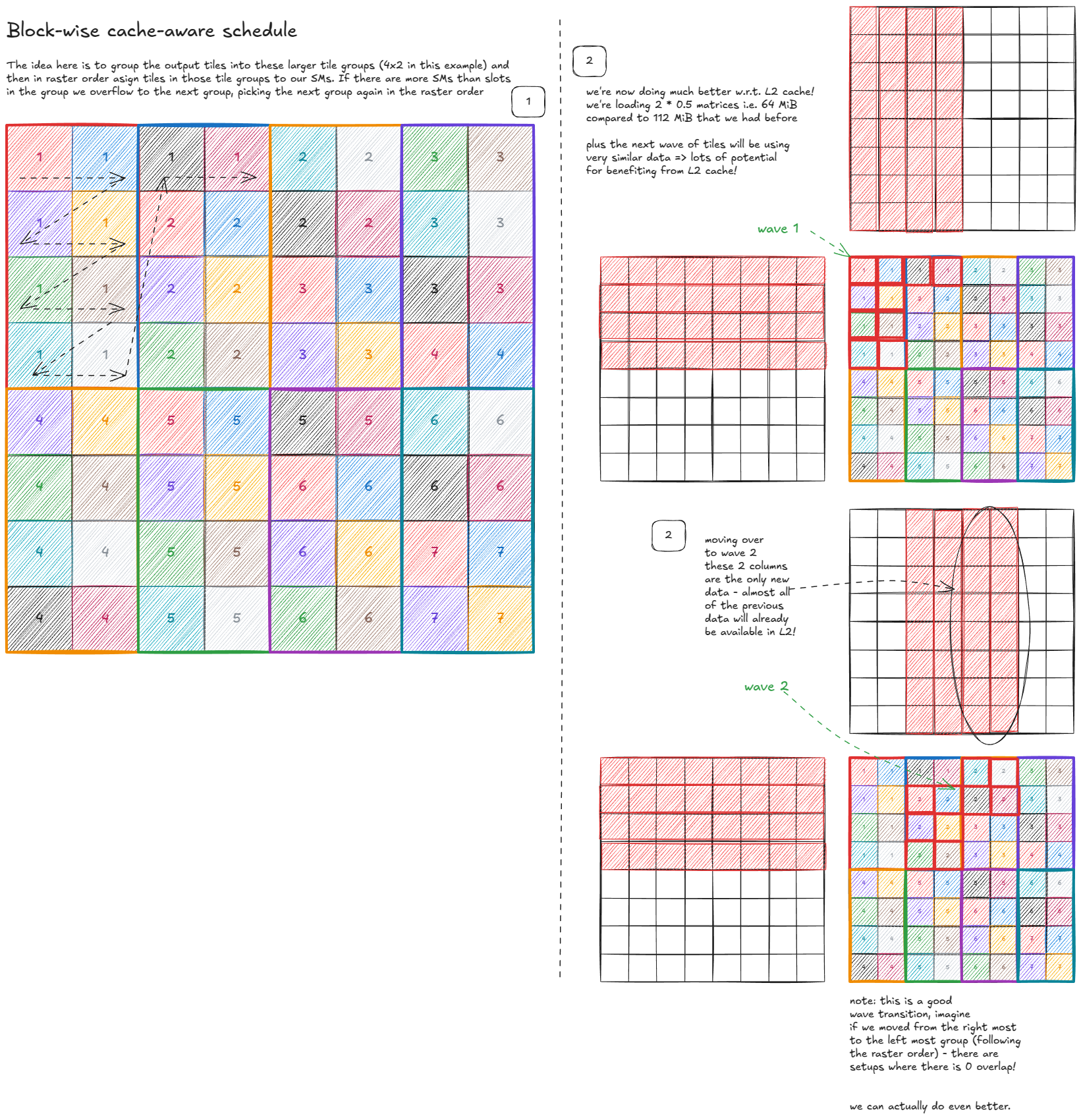
图 45：块级缓存感知调度

图 45：块级缓存感知调度

但我们能做得更好吗？令人惊讶的是，是的——通过使用空间填充曲线：

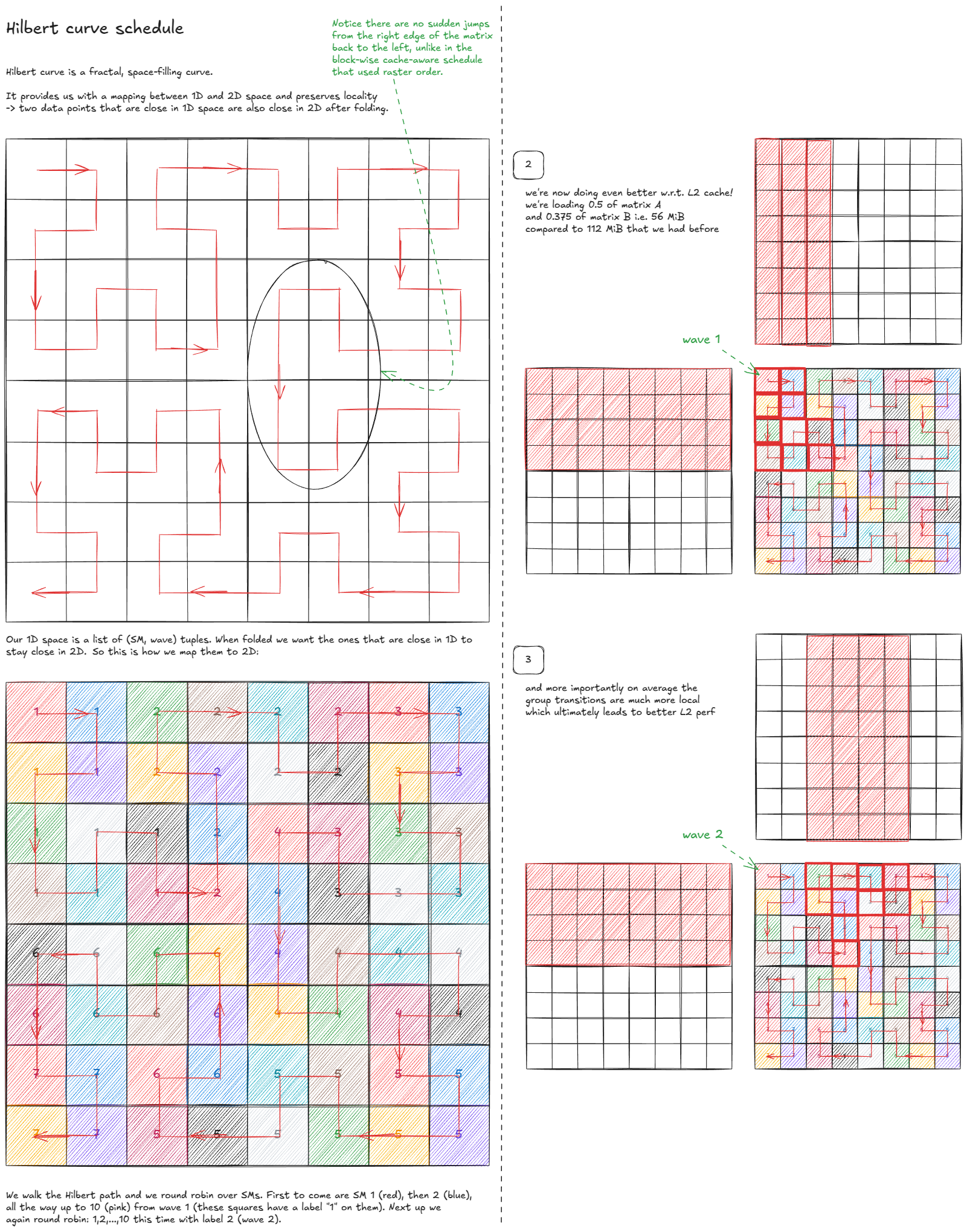
图 46：希尔伯特曲线调度

图 46：希尔伯特曲线调度

我将深入探讨的最后一个想法是利用 Hopper 新的集群级 CUDA 执行模型来减少 L2/GMEM 流量：

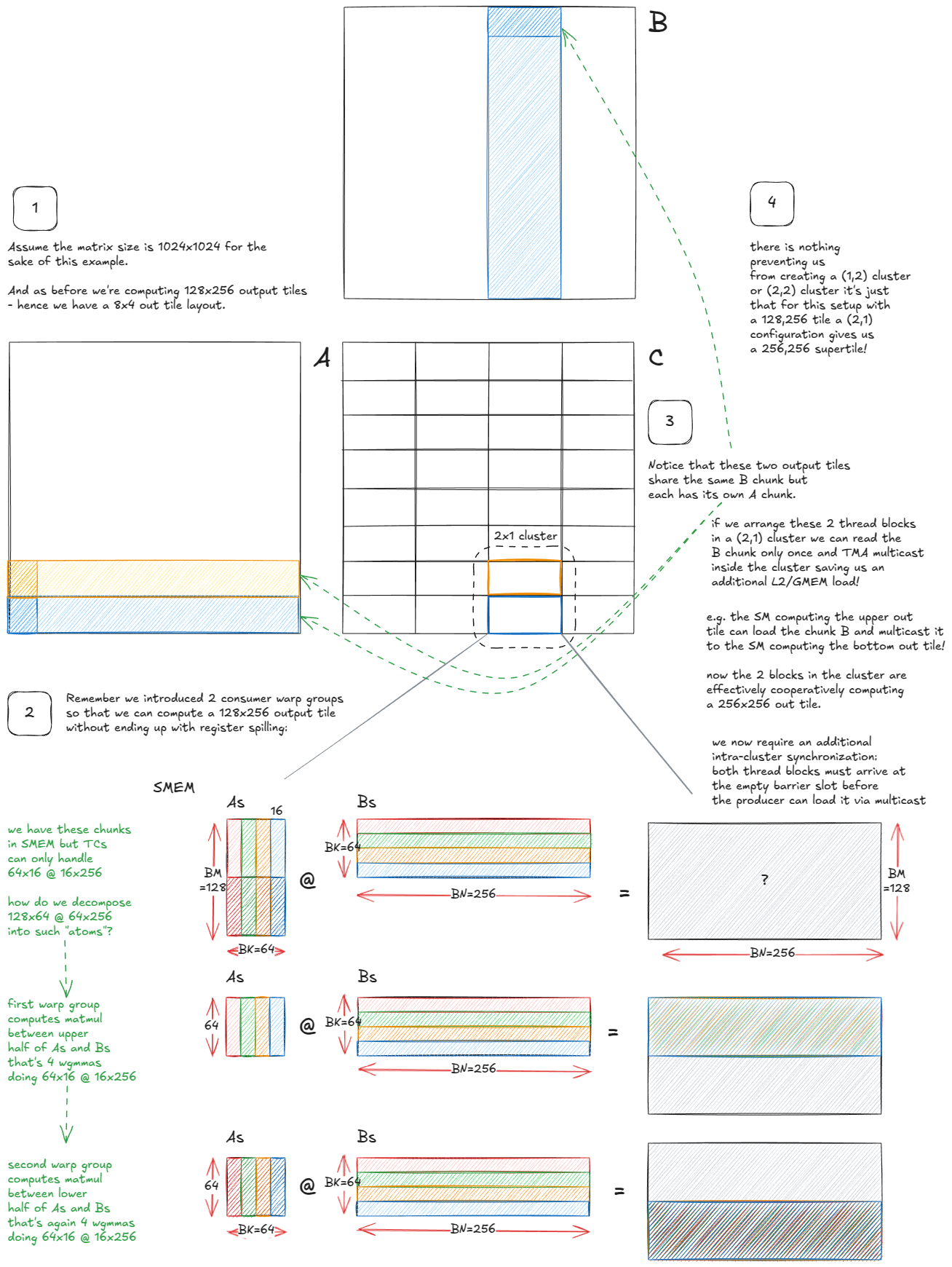
图 47：使用线程块集群减少 L2/GMEM 加载次数。

图 47：使用线程块集群减少 L2/GMEM 加载次数。

关键观察是，集群内的多个 SM 可以直接共享它们的 SMEM（通过 DSMEM），这让我们可以将集群视为一种“超级 SM”。

从调度角度看，没有根本性变化：不是每个 SM 处理自己独立的输出瓦片，而是整个集群协作处理一个更大的“超级瓦片”。算法的机制保持不变，但现在这些 SM 协调加载并重用彼此的数据。

由于希尔伯特曲线遍历已经设计为最大化局部性，超级 SM 可以遵循相同的遍历模式——只是粒度更粗。

最后，要超越 cuBLAS，我们必须收紧同步本身。到目前为止，我们在屏障上的到达/等待调用一直很浪费。

例如，消费者线程实际上不需要在full[qidx]上发出到达信号。唯一重要的条件是“所有字节都已到达”。丢弃这些冗余到达每次迭代节省 256 个令牌。类似地，对于empty[qidx]：一旦带有tid==0的消费者到达，生产者就可以安全地开始填充，因为消费者端（wgmma）在所有线程中同步执行。

一些额外的、低级别的技巧在实践中累积起来（本着 O(NR) 的精神）：

重新平衡寄存器：使用asm volatile("setmaxnreg.{inc,dec}.sync.aligned.u32 %0;\n" : : "n"(RegCount));将寄存器预算从生产者 warp 组（轻量级）转移到消费者 warp 组（wgmma 期间的重度用户）。
避免在输出时污染缓存。要么使用__stwt绕过 L1/L2，或者更好的是，进行异步存储：先溢出到 SMEM，然后让 TMA 异步复制到 GMEM。这将写回与计算重叠，就像我们在输入端所做的那样。
跳过冗余初始化：不是清零累加器寄存器，而是调整张量核心序列，使第一个 MMA 执行C = A @ B，后续 MMA 执行C = A @ B + C。

作为参考，以下是性能数字（来自 Pranjal 的博客），显示每个想法如何叠加在前一个之上：

优化	优化前性能（TFLOP/s）	优化后性能（TFLOP/s）
基线（warp-tiling） → 张量核心 + TMA	32	317
增加输出瓦片大小	317	423
流水线：重叠 TMA 加载与 TC 计算	423	498
瓦片增长：128×128 → 128×256（2 个消费者 warp 组）	498	610
持久化内核（隐藏存储延迟）	610	660
更快的 PTX 屏障	660	704
集群；TMA 多播	704	734
微优化	734	747
TMA 异步存储（寄存器 → SMEM → GMEM）	747	758
希尔伯特曲线调度	758	764