一种 TP-SP-EP 混合并行策略

发布于 2026-01-04 更新于 2026-04-07

3673 字

9 min read

标签： Sequence Parallel Distributed Parallel

在大模型训练中，单纯的张量并行（TP）或序列并行（SP）往往难以覆盖所有层的通信需求。对于稠密的 Attention 层，TP 可以高效地切分权重矩阵；而对于 MoE 层，专家并行（EP）才是降低通信开销的关键。本文梳理一种将 TP、SP、EP 融合的混合并行策略——重点剖析 Attention 层的两种 out_linear 方案，以及 MoE 层的 Dispatch / Combine 机制，帮助理解它们如何协同工作以最大化吞吐。

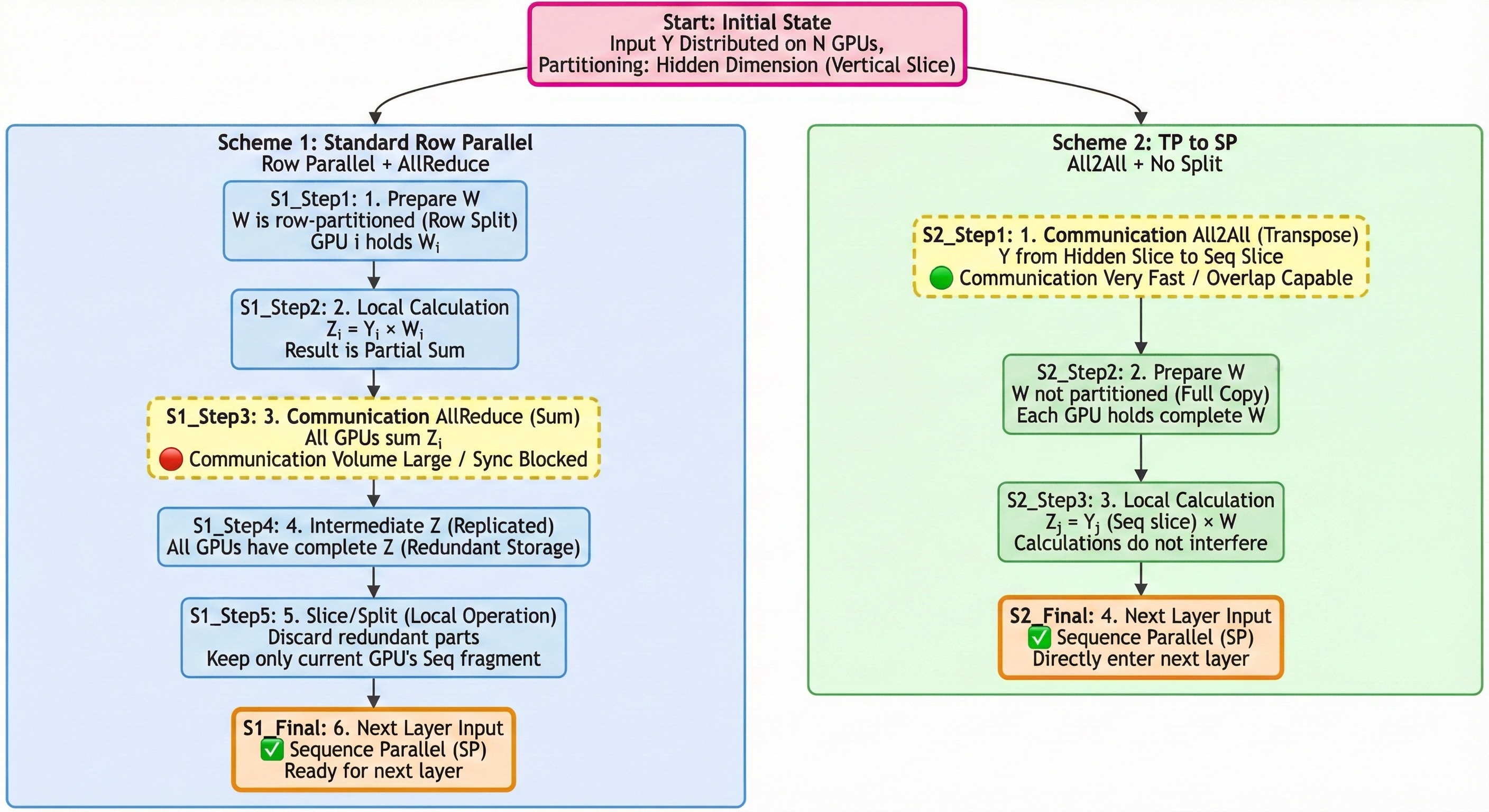
一、两种混合并行图示¶

非完整图示，不含后续 EP 并行 MoE 层。

上图展示了 Attention 层的两种 out_linear 实现路径。两条路径都从同一个列并行 qkv_linear 出发，区别在于如何处理输出投影：一种走行并行 + all_reduce，另一种走 all2all + 完整权重。后续的 MoE 层则统一以 SP 排布作为输入，借助两次 all2all 完成专家路由与聚合。

二、并行原理解析¶

两条方案的起点相同：列并行的 qkv_linear 将输出激活按隐藏层维度切分分布在各 GPU 上。从这一状态出发，两条路径以不同方式完成 out_linear 并进入序列并行段。

2.1 前提：`qkv_inear` (列切)¶

两种方案都始于一个列并行 (Column-Parallel) 的 qkv_inear 层。

我们有 $N$ 个 GPU。
输入 $X$ 是复制的 (replicated)。
第一个 qkv inear 层的权重 $A$ 被按列切分： $A = [A_1, A_2, \dots, A_N]$ 。
GPU $i$ 计算： $Y_i = \text{GeLU}(X A_i)$ 。
关键状态：计算完成后，中间激活 $Y = [Y_1, \dots, Y_N]$ 在 $N$ 个 GPU 上是按隐藏层维度（ $H_{\text{dim}}$ 维度，也常称为 $K$ 维度）切分的。

这里涉及到 Attention 的 TP 并行，原理可参考猛猿大佬文章 https://zhuanlan.zhihu.com/p/622212228，不再赘述。现在，我们要计算第二层 $Z = YW$ ，其中 $W$ 是 out_linear 的权重。

此时有两条路可走：继续保持 $H_{\text{dim}}$ 维度的切分（方案一），或提前通信将切分轴转到序列维度（方案二）。

2.2 方案一：`out_linear` (行切) + `all_reduce` + `Slice`¶

这个方案的核心思想是：保持 $H_{\text{dim}}$ 维度的切分。

数据排布：
- 输入 ( $Y$ )： $Y = [Y_1, \dots, Y_N]$ (按 $H_{\text{dim}}$ 切分)。
- 权重 ( $W$ )：out_linear 权重 $W$ 必须同样按 $H_{\text{dim}}$ 维度（即行）切分： $W = \begin{bmatrix} W_1 \\ W_2 \\ \vdots \\ W_N \end{bmatrix}$ 。
out_linear (局部计算)：
- GPU $i$ 拥有 $Y_i$ 和 $W_i$ 。
- 它只能计算它所拥有的那部分乘积： $Z_i = Y_i W_i$ 。
all_reduce (通信)：
- 根据矩阵乘法，最终结果是 $Z = YW = \sum_{i=1}^N Y_i W_i$ 。
- all_reduce 操作在所有 GPU 之间对 $Z_i$ 进行求和。
- $\text{AllReduce}(\{Z_1, \dots, Z_N\}) \to Z$ 。
完整的 $Z$ $Z$ ：
- $Z$ 在所有 GPU 上都是完整的、复制的 (replicated)。
每张 GPU 从 $Z$ 的行维度平均 Slice 出一部分，转为序列并行送到下一层。

优点：
- 节省内存：每个 GPU 只需要存储 $1/N$ 的 $W$ 权重。这在权重（如 $W_{\text{proj}}$ ）非常大时至关重要。
缺点：
- 通信瓶颈：必须在计算 $Z_i$ 之后执行一个 all_reduce。这是一个同步操作，通信量为 $Z$ 的大小，可能会阻塞流水线。

2.3 方案二：`all2all` + `out_linear` (不切分)¶

这是 “张量并行 (TP) 切换到序列并行 (SP)” 的策略。这个方案的核心思想是：通过通信改变数据的切分维度。

数据排布：
- 输入 ( $Y$ )： $Y = [Y_1, \dots, Y_N]$ (按 $H_{\text{dim}}$ 切分)。
- 权重 ( $W$ )：out_linear 权重 $W$ 不切分 (replicated)。每个 GPU 都有完整的 $W$ 。
all2all (通信)：
- 这一步的目标是将 $Y$ 的数据排布从“按 $H_{\text{dim}}$ 切分”转置为“按序列 (Sequence) 维度切分”。
- 之前：GPU $i$ 拥有 $Y_i$ （形状 $S \times (H_{\text{dim}}/N)$ ）。
- 操作：
  - GPU $i$ 将它的 $Y_i$ 沿着 $S$ 维度切成 $N$ 块： $Y_i = [Y_i^{(1)T}, \dots, Y_i^{(N)T}]^T$ 。
  - GPU $i$ 将 $Y_i^{(j)}$ 发送给 GPU $j$ 。
  - GPU $j$ 收到来自所有 $N$ 个 GPU 的 $\{Y_1^{(j)}, \dots, Y_N^{(j)}\}$ 。
- 之后：GPU $j$ 将收到的块沿着 $H_{\text{dim}}$ 维度拼接起来（⚠️：这里会有一个 transpose 操作），得到 $\hat{Y}_j = [Y_1^{(j)}, \dots, Y_N^{(j)}]$ （形状 $(S/N) \times H_{\text{dim}}$ ）。
- 结果： $Y$ 的排布从 $N$ 个 $S \times (K/N)$ 的块（TP）转换成了 $N$ 个 $(S/N) \times K$ 的块（SP）。
out_linear (局部计算)：
- GPU $j$ 拥有 $\hat{Y}_j$ (形状 $(S/N) \times H_{\text{dim}}$ ) 和完整的 $W$ (形状 $H_{\text{dim}} \times H_{\text{dim}}$ )。
- 它计算 $Z_j = \hat{Y}_j W$ 。
最终结果：
- $Z_j$ 的形状是 $(S/N) \times H_{\text{dim}}$ 。
- 最终输出 $Z$ 在 $N$ 个 GPU 上是按序列 (Sequence) 维度切分的。

在工程实现上，它们是两种完全不同的并行范式，有着根本的取舍：

特性	方案一 (out_linear [行切] + all_reduce)	方案二 (all2all + out_linear [不切分])
策略	标准行并行 (Row-Parallelism)	张量并行 (TP) $\to$ 序列并行 (SP) 转换
`out_linear` 权重 $W$	按行切分 (节省 $N-1/N$ 内存)	不切分/复制 (需要 $N$ 倍内存)
通信操作	`all_reduce` (在计算之后)	`all2all` (在计算之前)
通信内容	输出 $Z$ (形状 $S \times H_{\text{dim}}$ )	激活 $Y$ (形状 $S \times H_{\text{dim}}$ )
输出 $Z$ 的排布	复制的 (Replicated)	按序列切分 (Sequence-Parallel)

结论：方案二牺牲了 $W$ 的内存（现在需要 $N$ 份 $W$ ），来换取将并行维度从 $H_{\text{dim}}$ (TP) 切换到 $S$ (SP)，其主要手段是用 all2all 替代 all_reduce，并利用通信-计算重叠来提升流水线效率。

三、通信量对比分析¶

通信量是决定这两种方案性能的关键因素。我们来详细分析一下，假设：

$N$ = GPU 数量 (TP 规模)
$H_{\text{dim}}$ = 隐藏层维度
$d$ = 数据类型大小 (例如 bfloat16 为 2 字节)

3.1 方案一：`out_linear` (行切) + `all_reduce`¶

目标：计算 $Z = \sum Z_i$ 并将 $Z$ 分发回所有 GPU。
通信对象：张量 $Z_i$ ，其大小为 $S \times H_{\text{dim}} \times d$ 。
通信量分析：
- 在标准的 ring-allreduce 中，每个 GPU 在 $N-1$ 步中发送数据，在 $N-1$ 步中接收数据。
- 为了完成求和与分发，每个 GPU 最终发送的总数据量约为 $\frac{N-1}{N} \times (S \times H_{\text{dim}} \times d)$ ，接收的总数据量也约为 $\frac{N-1}{N} \times (S \times H_{\text{dim}} \times d)$ 。
- 每 GPU 的总通信量 (发送+接收)： $V_1 = 2 \times \frac{N-1}{N} \times (S \times H_{\text{dim}} \times d)$

3.2 方案二：`all2all` + `out_linear` (不切分)¶

目标：将 $Y$ 的切分方式从 $H_{\text{dim}}$ 维度 (TP) 转换为 $S$ 维度 (SP)。
通信对象：张量 $Y_i$ ，其大小为 $S \times (H_{\text{dim}}/N) \times d$ 。
通信量分析：
- all2all 操作中，每个 GPU $i$ 将其本地的 $Y_i$ (形状 $S \times (H_{\text{dim}}/N)$ ) 切分为 $N$ 块，每块 $Y_i^{(j)}$ (形状 $(S/N) \times (H_{\text{dim}}/N)$ )。
- GPU $i$ 将 $N-1$ 块发送给其他 $N-1$ 个 GPU。
- GPU $i$ 发送的总数据量为： $(N-1) \times \text{size}(Y_i^{(j)}) = (N-1) \times (\frac{S}{N} \times \frac{H_{\text{dim}}}{N}) \times d$ 。
- 同理，它也接收 $N-1$ 块。
- 每 GPU 的总通信量 (发送+接收)：
  
  $V_2 = 2 \times (N-1) \times (\frac{S \times H_{\text{dim}}}{N^2}) \times d = \frac{2(N-1)}{N^2} \times (S \times H_{\text{dim}} \times d)$

对比¶

方案	通信操作	每 GPU 总通信量 ( V )
方案一	`all_reduce`	$V_1 = \frac{2(N-1)}{N} \times (S \cdot H_{\text{dim}} \cdot d)$
方案二	`all2all`	$V_2 = \frac{2(N-1)}{N^2} \times (S \cdot H_{\text{dim}} \cdot d)$

得出： $V_2 = \frac{1}{N} \times V_1$ 。因此，方案二 (**all2all**) 在通信总量上具有明显优势。

除此之外，选择方案二还有其他的原因：

通信模式：all_reduce 包含计算（Sum），而 all2all 只是数据交换（Transpose）。在某些硬件拓扑（如 NVLink Switch）上，all2all 几乎可以达到线速，效率极高。
通信重叠：方案二的 all2all 作用于 $Y$ ，它可以在 $Y$ 被计算时重叠 (Overlap) 进行。方案一的 all_reduce 必须等待 out_linear 计算 $Z_i$ 完成后才能开始。
内存代价：方案二的优势是有代价的。它需要每个 GPU 都存储完整的 out_linear 权重 $W$ ，而方案一只需要 $1/N$ 的权重。
序列并行 (SP)：如果你的网络架构（例如 MoE EP 并行）被优化为在序列并行的输入上工作，那么方案二的输出（ $Z$ 按序列切分）可以直接喂给下一层，完全消除了后续对 $Z$ 进行 all_reduce 或 allgather 的需求。

四、EP 并行的 MoE 层¶

无论选择方案一还是方案二，进入 MoE 层时激活都已处于序列并行（SP）的排布——每张 GPU 持有全局序列的 $1/P$ 片段，形状为 $\frac{S}{P} \times H_{\text{dim}}$ 。EP 的核心思想是将专家参数分片到各 GPU，同时通过两次 all2all 完成 token 的路由与聚合，以此避免所有 GPU 都冗余存储全量专家权重。

4.1 假设一些参数：¶

输入： $X \in \mathbb{R}^{S \times H_{\text{dim}}}$
Router：为每个 token 选 $k$ $k$ 个专家（Top-k），得到
- 专家索引： $\text{eid} \in \{0,\dots,E-1\}^{S \times k}$
- 权重： $w \in \mathbb{R}^{S \times k}$
专家集合：共有 $E$ 个 experts
EP 规模： $P$ $P$ （同一个 EP group 中有 $P$ $P$ 张 GPU）
- 每张 GPU 持有 $E/P$ 个 experts（参数分片）

两次 all2all****（Dispatch / Combine）：

EP 的本质是：按专家维度切参数，但按 token 路由把激活在卡间重排。因此每个 MoE 层固定两次集合通信。

Dispatch：把 token 送到“持有目标专家”的 GPU
Combine：把专家输出送回“token 所在的 GPU”，并按权重聚合

MoE 输入的 SP 排布：

全局 $S$ $S$ 个 tokens，被 $P$ $P$ 张 GPU 按序列维度均分
- GPU $i$ 拥有： $X_i \in \mathbb{R}^{\frac{S}{P} \times H_{\text{dim}}}$
每个 GPU 本地计算 Router：
- $\text{eid}_i \in \{0,\dots,E-1\}^{\frac{S}{P} \times k}$
- $w_i \in \mathbb{R}^{\frac{S}{P} \times k}$

4.2 Dispatch：`permute` + `all2all`（把 token 发到专家所在卡）¶

目标：将 token 从“按序列切分”的排布，变换为“按专家分桶并落在对应 GPU”的排布。

本地分桶（bucketize）/ 打包（pack）：

对 GPU $i$ 上的每个 token $t$ ，它会被路由到 $k$ 个专家： ${\text{eid}_i[t,1], \dots, \text{eid}_i[t,k]}$
定义专家到 GPU 的映射（静态）：
- $\text{owner}(e) \in \{0,\dots,P-1\}$
GPU $i$ $i$ 将其本地 token 复制出 $k$ $k$ 份“token-expert 关联样本”，并按 $\text{owner}(e)$ $owner (e)$ 分桶：
- 形成 $P$ 个发送缓冲区： $\text{sendbuf}_{i\to j}$
同时，GPU $i$ $i$ 记录两类索引用于还原：
- src_slot：这个样本来自本地第几个 token
- k_slot：这是 top-k 的第几路（用于乘权重）

第一次all2all：

所有 GPU 同时执行 all2all， $\text{recvbuf}_{j} = \bigcup_{i=0}^{P-1} \text{sendbuf}_{i\to j}$

Dispatch 后的数据排布：

GPU $j$ $j$ 得到按其本地 experts 分桶后的激活集合：
- $\hat{X}_j \in \mathbb{R}^{M_j \times H_{\text{dim}}}$
其中 $M_j$ 是路由到 GPU $j$ 的（token, expert）样本数（一般不均匀）。
同时携带对应的还原元信息（如 src_slot / k_slot、以及回传路由所需的 index）。

关键状态：Dispatch 后，激活不再保持原序列顺序，而是按专家分桶组织，便于专家侧批处理。

4.3 Experts：本地 `grouped_gemm`（只在持有的专家上算）¶

GPU $j$ 持有专家集合，每个专家是一个 FFN：

Expert $e$ 的参数： $W^{(e)}_1, W^{(e)}_2$
对属于该专家的子 batch： $\hat{X}^{(e)}_j$
局部计算：
- $H^{(e)} = \phi(\hat{X}^{(e)}_j W^{(e)}_1)$
- $O^{(e)} = H^{(e)} W^{(e)}_2$

将所有专家输出拼接为：

$\hat{O}_j \in \mathbb{R}^{M_j \times H_{\text{dim}}}$ （与 $\hat{X}_j$ 一一对应）

4.4 Combine：`all2all` + `unpermute` + `weighted_sum`（送回并聚合）¶

目标：把专家输出返回到 token 的原属 GPU，并将 top-k 多路输出按权重聚合为一个 token 输出。

按来源 GPU 反向打包（pack-back）：

Dispatch 时每个样本带有其“来源 GPU + 来源 token 位置（src_slot）+ k_slot”
GPU $j$ $j$ 将 $\hat{O}_j$ $\hat{O}_{j}$ 按来源 GPU 分桶：
- 形成 $\text{sendback}_{j\to i}$

第二次 all2all：

所有 GPU 同时执行 all2all，GPU $i$ 收到所有返回样本集合 $\text{recvback}_i$

本地还原与加权聚合：

GPU $i$ 对其本地每个 token $t$ ，收集来自 $k$ 路的返回输出 ${O_{t,1},\dots,O_{t,k}}$
按 router 权重聚合：
- $Y_i[t] = \sum_{r=1}^{k} w_i[t,r] \cdot O_{t,r}$

Combine 后的输出排布：

GPU $i$ $i$ 得到：
- $Y_i \in \mathbb{R}^{\frac{S}{P} \times H_{\text{dim}}}$
输出仍是按序列维度切分（SP），可直接送入下一层。

五、全局数据流回顾¶

将各阶段的排布变化串联起来，便能看清整条流水线的”数据拓扑”：

阶段	数据排布	通信
`qkv_linear` 输入	序列切分 (SP)， $(S/N) \times H$	—
`qkv_linear` 输出（列并行）	隐藏维切分 (TP)， $S \times (H/N)$	无（本地计算）
方案一 `out_linear`（行并行）输出	全量复制， $S \times H$	`all_reduce`
→ Slice 为 SP	序列切分， $(S/N) \times H$	本地切片
方案二 `all2all` 后	序列切分 (SP)， $(S/N) \times H$	`all2all`
→ `out_linear`（完整权重）输出	序列切分， $(S/N) \times H$	无
MoE Dispatch `all2all`	专家分桶， $M_j \times H$ （不均匀）	`all2all`
Expert `grouped_gemm`	专家分桶， $M_j \times H$	无（本地计算）
MoE Combine `all2all`	序列切分， $(S/P) \times H$	`all2all`

可以看到：两条路径都将 Attention 层的 TP 激活”归还”为 SP，从而 MoE 层可以无缝地以序列并行为接口完成 EP 路由，整个前向过程不需要任何额外的同步等待（在理想的通信-计算重叠实现下）。

六、总结¶

方案一（行并行 + all_reduce）：实现简单，权重内存占用低（ $1/N$ ），但 all_reduce 必须在 out_linear 完成后才能发起，难以与计算重叠。
方案二（all2all + 完整权重）：通信量降为方案一的 $1/N$ ，且 all2all 可与前一步计算重叠；代价是每张 GPU 需存储完整的 out_linear 权重。当 GPU 显存充裕、NVLink 带宽高、且下游对 SP 排布有明确需求时（如接 EP-MoE），方案二的优势更为突出。
EP 的 MoE 层：以 SP 排布为接口，两次 all2all 完成 Dispatch 与 Combine，实现专家参数的分片存储与正确的 token 路由，输出依然是 SP，可无缝接入下一 Transformer 层。