Writing Speed-of-Light Flash Attention for 5090 in CUDA C++

📝 转载 / 引用来源: 作者 Thien Tran · 查看原文
Writing Speed-of-Light Flash Attention for 5090 in CUDA C++¶
在这篇文章中,我将介绍如何在 CUDA C++ 中为 5090 实现 Flash Attention。主要目标是学习在 CUDA C++ 中编写注意力机制,因为许多特性在 Triton 中不可用,例如 sm120 的 MXFP8 / NVFP4 MMA。我还认为这是学习 matmul 内核后的自然下一步。最后,有很多优秀的博客文章 介绍如何编写快速 matmul 内核,但没有关于注意力机制的。所以我想借此机会写点好东西。
强烈建议读者熟悉 CUDA C++ 以及如何在 NVIDIA GPU 上使用 Tensor 核心。当然,你仍然可以继续阅读,并在过程中使用你最喜欢的 LLM 进行澄清。或者你可以查看 GPU-MODE 系列(幻灯片,YouTube)以获得基础的 CUDA C++ 知识,以及上面提到的优秀 matmul 博客文章,以快速上手。
你可以在这里找到本文讨论的完整实现:https://github.com/gau-nernst/learn-cuda/tree/e83c256/07_attention。对于 bs=1, num_heads=8, len_query=4096, len_kv = 8192,5090 @ 400W,使用 CUDA 12.9 编译,我获得了以下基准测试结果(5090 的理论极限为 209.5 TFLOPS,针对 BF16)
| Kernel | TFLOPS | % of SOL |
|---|---|---|
F.sdpa() (Flash Attention) | 186.73 | 89.13% |
F.sdpa() (CuDNN) | 203.61 | 97.19% |
flash-attn | 190.58 | 90.97% |
| v1 (basic) | 142.87 | 68.20% |
| v2 (shared memory swizzling) | 181.11 | 86.45% |
| v3 (2-stage pipelining) | 189.84 | 90.62% |
v4 (ldmatrix.x4 for K and V) | 194.33 | 92.76% |
| v5 (better pipelining) | 197.74 | 94.39% |
请注意,尽管我在这些实现中只使用了 Ampere 特性(sm120 支持 cp.async.bulk 即 TMA,但我在这里没有使用它),我的实现可能无法在早期一代的 GPU 上高效运行。由于新硬件的改进,你可能需要使用更多技巧才能在旧 GPU 上达到理论极限速度,例如流水线化 shared memory 到 register memory 的数据移动。
Flash Attention 算法¶
让我们从注意力机制的参考实现开始。
from torch import Tensor
def sdpa(q: Tensor, k: Tensor, v: Tensor):
# q: [B, Lq, DIM]
# k: [B, Lk, DIM]
# v: [B, Lk, DIM]
D = q.shape[-1]
scale = D ** -0.5
attn = (q @ k.transpose(-1, -2)) * scale # [B, Lq, Lk]
attn = attn.softmax(dim=-1)
out = attn @ v # [B, Lq, DIM]
return outfrom torch import Tensor
def sdpa(q: Tensor, k: Tensor, v: Tensor):
# q: [B, Lq, DIM]
# k: [B, Lk, DIM]
# v: [B, Lk, DIM]
D = q.shape[-1]
scale = D ** -0.5
attn = (q @ k.transpose(-1, -2)) * scale # [B, Lq, Lk]
attn = attn.softmax(dim=-1)
out = attn @ v # [B, Lq, DIM]
return out从技术上讲,如果输入是 BF16,某些计算应该保持在 FP32,特别是 softmax。但是,为了简洁起见,我们省略了它们。
我们正在实现 Flash Attention 2 论文 中概述的算法。每个 threadblock 负责 Q 的一个块,我们将沿着 KV 的序列长度进行迭代。算法的类 Python 概要如下所示(S 和 P 遵循 Flash Attention 符号)。
scale = DIM ** -0.5
for b_idx in range(B):
for tile_Q_idx in range(Lq // BLOCK_Q):
### start of each threadblock's kernel
tile_O = torch.zeros(BLOCK_Q, DIM)
tile_Q = load_Q(b_idx, tile_Q_idx) # [BLOCK_Q, DIM]
for tile_KV_idx in range(Lk // BLOCK_KV):
# first MMA: S = Q @ K.T
# (BLOCK_Q, DIM) x (BLOCK_KV, DIM).T -> (BLOCK_Q, BLOCK_KV)
tile_Q # (BLOCK_Q, DIM)
tile_K = load_K(b_idx, tile_KV_idx) # (BLOCK_KV, DIM)
tile_S = tile_Q @ tile_K.T # (BLOCK_Q, BLOCK_KV)
tile_S = tile_S * scale
# online softmax and rescale tile_O
...
# second MMA: O = P @ V
# (BLOCK_Q, BLOCK_KV) x (BLOCK_KV, DIM) -> (BLOCK_Q, DIM)
tile_P # (BLOCK_Q, BLOCK_KV)
tile_V = load_V(b_idx, tile_KV_idx) # (BLOCK_KV, DIM)
tile_O += tile_P @ tile_V # (BLOCK_Q, DIM)
# normalize output and write results
store_O(b_idx, tile_Q_idx)
### end of each threadblock's kernelscale = DIM ** -0.5
for b_idx in range(B):
for tile_Q_idx in range(Lq // BLOCK_Q):
### start of each threadblock's kernel
tile_O = torch.zeros(BLOCK_Q, DIM)
tile_Q = load_Q(b_idx, tile_Q_idx) # [BLOCK_Q, DIM]
for tile_KV_idx in range(Lk // BLOCK_KV):
# first MMA: S = Q @ K.T
# (BLOCK_Q, DIM) x (BLOCK_KV, DIM).T -> (BLOCK_Q, BLOCK_KV)
tile_Q # (BLOCK_Q, DIM)
tile_K = load_K(b_idx, tile_KV_idx) # (BLOCK_KV, DIM)
tile_S = tile_Q @ tile_K.T # (BLOCK_Q, BLOCK_KV)
tile_S = tile_S * scale
# online softmax and rescale tile_O
...
# second MMA: O = P @ V
# (BLOCK_Q, BLOCK_KV) x (BLOCK_KV, DIM) -> (BLOCK_Q, DIM)
tile_P # (BLOCK_Q, BLOCK_KV)
tile_V = load_V(b_idx, tile_KV_idx) # (BLOCK_KV, DIM)
tile_O += tile_P @ tile_V # (BLOCK_Q, DIM)
# normalize output and write results
store_O(b_idx, tile_Q_idx)
### end of each threadblock's kernel这里隐含的意思是 DIM 很小,这样我们可以在整个内核执行期间将 tile_Q 保持在 register memory 中。这就是为什么现在几乎所有模型都使用 head_dim=128。当然也有例外,比如 MLA,它对 Q 和 K 使用 head_dim=576,对 V 使用 head_dim=512。说到这个,我哪天应该研究一下 FlashMLA。
在线 softmax 的解释相当复杂,所以让我们推迟这部分的解释。在高层次上,你只需要知道在线 softmax 会将 tile_S 转换为 tile_P,并且还会重新缩放 tile_O。
版本 1 - 基础实现¶
我们将遵循典型的 MMA 流程
- 使用 cp.async 从 global memory 加载二维 tile 数据到 shared memory。这需要 Ampere(sm80 及更新版本)。
- 使用 ldmatrix 从 shared memory 加载数据到 register memory。
- 调用 mma.m16n8k16 进行 BF16 矩阵乘法(并累加)。
我想首先专注于正确实现算法,因此我省略了更复杂的技巧,如 shared memory swizzling 和流水线化。这减少了出错的可能性,我们稍后会在性能优化时重新讨论它们。
Global 到 Shared memory 的数据传输¶
以下模板函数执行从 global memory 到 shared memory 的二维 tile 复制。
- 二维 tile 的形状通过
HEIGHT和WIDTH指定。 dst是 shared memory 地址,src是 global memory 地址。- Global memory
src是行优先的,因此src_stride指定移动到下一行需要移动多少。 - Shared memory
dst也是行优先的,并将作为连续块存储 ->dst_stride = WIDTH。
#include <cuda_bf16.h>
template <int HEIGHT, int WIDTH, int TB_SIZE>
__device__ inline
void global_to_shared(uint32_t dst, const nv_bfloat16 *src, int src_stride, int tid) {
constexpr int num_elems = 16 / sizeof(nv_bfloat16);
constexpr int num_iters = HEIGHT * WIDTH / (TB_SIZE * num_elems);
for (int iter = 0; iter < num_iters; iter++) {
const int idx = (iter * TB_SIZE + tid) * num_elems;
const int row = idx / WIDTH;
const int col = idx % WIDTH;
const uint32_t dst_addr = dst + (row * WIDTH + col) * sizeof(nv_bfloat16);
const nv_bfloat16 *src_addr = src + (row * src_stride + col);
asm volatile("cp.async.cg.shared.global [%0], [%1], 16;" :: "r"(dst_addr), "l"(src_addr));
}
}#include <cuda_bf16.h>
template <int HEIGHT, int WIDTH, int TB_SIZE>
__device__ inline
void global_to_shared(uint32_t dst, const nv_bfloat16 *src, int src_stride, int tid) {
constexpr int num_elems = 16 / sizeof(nv_bfloat16);
constexpr int num_iters = HEIGHT * WIDTH / (TB_SIZE * num_elems);
for (int iter = 0; iter < num_iters; iter++) {
const int idx = (iter * TB_SIZE + tid) * num_elems;
const int row = idx / WIDTH;
const int col = idx % WIDTH;
const uint32_t dst_addr = dst + (row * WIDTH + col) * sizeof(nv_bfloat16);
const nv_bfloat16 *src_addr = src + (row * src_stride + col);
asm volatile("cp.async.cg.shared.global [%0], [%1], 16;" :: "r"(dst_addr), "l"(src_addr));
}
}从 Global memory 到 Shared memory 的二维 tile 复制。
我们将使用内联汇编来编写 cp.async.cg.shared.global。这个 PTX 指令为每个 CUDA 线程执行 16 字节传输,即 8 个 BF16 元素(num_elems = 16 / sizeof(nv_bfloat16))。为了确保合并内存访问,连续的线程将负责连续的 8xBF16 组。
连续的线程负责连续的 8xBF16 组。
注意:
- 循环
for (int iter = 0; iter < num_iters; iter++)这样写是为了让编译器(nvcc)可以完全展开循环。num_iters在编译时已知(由constexpr保证)。如果我们在循环中混入tid,对编译器来说它是一个”动态”变量,即使我们知道变量的某些约束(即tid < TB_SIZE),循环也无法展开。 - shared memory 指针
dst的数据类型是uint32_t。这是有意为之的。几乎所有 PTX 指令都期望 shared memory 地址位于 shared state space 中。我们可以使用static_cast<uint32_t>(__cvta_generic_to_shared(ptr))将 C++ 指针(通用地址)转换为 shared state space 地址。这是在global_to_shared()外部完成的。
要完成 cp.async 的使用,我们还需要添加以下内容:
cp.async.commit_group(PTX):将之前发出的所有cp.async指令提交到一个cp.async组。这个组将成为同步的单位。cp.async.wait_all(PTX):等待所有已提交的组完成。__syncthreads():确保(threadblock 中的)所有线程在读取 shared memory 中加载的数据之前都到达这里(因为一个线程可能读取另一个线程加载的数据)。更重要的是,这会将新数据的可见性广播给 threadblock 中的所有线程。没有__syncthreads(),编译器可以自由地优化掉内存访问。
一如既往,请参考 PTX 文档 获取有关指令的更多信息。基本上,我们发出多个 cp.async 并在之后立即等待它们完成。commit_group 和 wait_group 为我们提供了一种机制来稍后实现流水线化。但现在,只需知道我们必须这样写才能使用 cp.async。
我们的代码片段看起来像这样。
// nv_bfloat16 *Q;
// uint32_t Q_smem;
// const int tid = blockIdx.x;
// constexpr int TB_SIZE = 32 * 4;
// constexpr int DIM = 128;
global_to_shared<BLOCK_Q, DIM, TB_SIZE>(Q_smem, Q, DIM, tid);
asm volatile("cp.async.commit_group;");
asm volatile("cp.async.wait_all;");
__syncthreads();// nv_bfloat16 *Q;
// uint32_t Q_smem;
// const int tid = blockIdx.x;
// constexpr int TB_SIZE = 32 * 4;
// constexpr int DIM = 128;
global_to_shared<BLOCK_Q, DIM, TB_SIZE>(Q_smem, Q, DIM, tid);
asm volatile("cp.async.commit_group;");
asm volatile("cp.async.wait_all;");
__syncthreads();Shared memory 到 Register memory 的数据传输¶
在进行全局到共享内存的数据传输时,我们以 threadblock tile 和单个 CUDA 线程为单位来思考。对于共享内存到寄存器的数据传输,由于这是为了服务后续的 MMA 指令,我们以 warp tile/MMA tile 和 warp 为单位来思考。遵循 Flash Attention 2(第 3.3 节),我们让线程块中的每个 warp 处理一部分 tile_Q,沿着 Q 序列长度维度进行分割。这意味着不同的 warp 将索引到 tile_Q 的不同块,但它们都索引到相同的 tile_K 和 tile_V 块在 KV 序列长度循环中。
Flash Attention 2 中的 warp 分区。
由于我们使用 mma.m16n8k16 指令,每个 MMA 16x8 输出 tile(m16n8)需要一个 16x16 的 A tile(m16k16)和一个 8x16 的 B tile(n8k16)。ldmatrix 可以加载一个、两个或四个 8x8 tile 的 16 位元素。因此,
- A tile
m16k16需要四个 8x8 tile ->ldmatrix.x4 - B tile
n8k16需要两个 8x8 tile ->ldmatrix.x2
只有 Q 在 MMA 中充当 A。K 和 V 都在各自的 MMA 中充当 B,尽管 K 需要转置的 ldmatrix 以获得正确的布局(所有张量在全局和共享内存中使用行优先布局)。
要使用 ldmatrix,每个线程提供一行的地址。线程 0-7 选择第一个 8x8 tile,线程 8-15 选择第二个 8x8 tile,依此类推。A 的布局 在官方的 PTX 文档中可能看起来令人困惑。但更容易(至少对我来说)专注于 MMA tile 内 8x8 tile 的顺序。
mma.m16n8k16 中 ldmatrix tile 的顺序。
通过上面的可视化,我希望以下代码片段有意义
constexpr int MMA_M = 16;
constexpr int MMA_N = 8;
constexpr int MMA_K = 16;
uint32_t Q_smem;
uint32_t Q_rmem[WARP_Q / MMA_M][DIM / MMA_K][4];
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
const int row = (warp_id * WARP_Q) + (mma_id_q * MMA_M) + (lane_id % 16);
const int col = (mma_id_d * MMA_K) + (lane_id / 16 * 8);
const uint32_t addr = Q_smem + (row * DIM + col) * sizeof(nv_bfloat16);
ldmatrix_x4(Q_rmem[mma_id_q][mma_id_d], addr);
}constexpr int MMA_M = 16;
constexpr int MMA_N = 8;
constexpr int MMA_K = 16;
uint32_t Q_smem;
uint32_t Q_rmem[WARP_Q / MMA_M][DIM / MMA_K][4];
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
const int row = (warp_id * WARP_Q) + (mma_id_q * MMA_M) + (lane_id % 16);
const int col = (mma_id_d * MMA_K) + (lane_id / 16 * 8);
const uint32_t addr = Q_smem + (row * DIM + col) * sizeof(nv_bfloat16);
ldmatrix_x4(Q_rmem[mma_id_q][mma_id_d], addr);
}- 两个嵌套循环将
[MMA_M, MMA_K](即[16, 16])在共享内存中 tile 化[WARP_Q, DIM]。 (warp_id * WARP_Q)选择 warp tile。我们不需要为 K 和 V 这样做。(mma_id_q * MMA_M)在row和(mma_id_d * MMA_K)在col中选择 MMA tile。(lane_id % 16)在row和(lane_id / 16 * 8)在col中为每个线程选择正确的行地址,遵循所需的 Multiplicand A 布局(见上图)。
ldmatrix_x4() 是 ldmatrix.sync.aligned.m8n8.x4.b16 PTX 的一个小包装,为了方便。你可以参考 common.h 获取更多细节。
K 和 V 可以类似地从共享内存加载到寄存器内存。需要注意的一点是使用 ldmatrix 时的行优先/列优先布局。无论是否使用 .trans 修饰符,每个线程仍然提供 8x8 tile 中每行的行地址。.trans 只改变结果的寄存器布局 ldmatrix。
对 V 使用转置版本的 ldmatrix。
一个判断是否使用转置版本的技巧是查看 K 维度或归约维度。第一个 MMA 的 K 维度沿着 ldmatrix 维度,而第二个 MMA 的 K 维度沿着 DIM 维度。BLOCK_KV。
草稿版本¶
我们有了高层级的基于 tile 的设计,并知道如何为 MMA 加载数据。调用 MMA 很简单——只需在我们的代码中插入 mma.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32 PTX。我们的草稿版本看起来像这样。
constexpr int BLOCK_Q = 128;
constexpr int BLOCK_KV = 64;
constexpr int DIM = 128;
constexpr int NUM_WARPS = 4;
constexpr int TB_SIZE = NUM_WARPS * 32;
// mma.m16n8k16
constexpr int MMA_M = 16;
constexpr int MMA_N = 8;
constexpr int MMA_K = 16;
__global__
void attention_v1_kernel(
const nv_bfloat16 *Q, // [bs, len_q, DIM]
const nv_bfloat16 *K, // [bs, len_kv, DIM]
const nv_bfloat16 *V, // [bs, len_kv, DIM]
nv_bfloat16 *O, // [bs, len_q, DIM]
int bs,
int len_q,
int len_kv) {
// basic setup
const int tid = threadIdx.x;
const int warp_id = tid / 32;
const int lane_id = tid % 32;
// increment Q, K, V, O based on blockIdx.x
...
// set up shared memory
// Q_smem is overlapped with (K_smem + V_smem), since we only use Q_smem once
extern __shared__ uint8_t smem[];
const uint32_t Q_smem = __cvta_generic_to_shared(smem);
const uint32_t K_smem = Q_smem;
const uint32_t V_smem = K_smem + BLOCK_KV * DIM * sizeof(nv_bfloat16);
// FA2: shard BLOCK_Q among warps
constexpr int WARP_Q = BLOCK_Q / NUM_WARPS;
// set up register memory
uint32_t Q_rmem[WARP_Q / MMA_M][DIM / MMA_K][4]; // act as A in MMA
uint32_t K_rmem[BLOCK_KV / MMA_N][DIM / MMA_K][2]; // act as B in MMA
uint32_t P_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_K][4]; // act as A in MMA
uint32_t V_rmem[BLOCK_KV / MMA_K][DIM / MMA_N][2]; // act as B in MMA
float O_rmem[WARP_Q / MMA_M][DIM / MMA_N][4]; // act as C/D in MMA
// Q global->shared [BLOCK_Q, DIM]
global_to_shared<BLOCK_Q, DIM, TB_SIZE>(Q_smem, Q, DIM, tid);
asm volatile("cp.async.commit_group;");
asm volatile("cp.async.wait_all;");
__syncthreads();
// Q shared->register. select the correct warp tile
// Q stays in registers throughout the kernel's lifetime
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
const int row = warp_id * WARP_Q + mma_id_q * MMA_M + (lane_id % 16);
const int col = mma_id_d * MMA_K + (lane_id / 16 * 8);
const uint32_t addr = Q_smem + (row * DIM + col) * sizeof(nv_bfloat16);
ldmatrix_x4(Q_rmem[mma_id_q][mma_id_d], addr);
}
__syncthreads();
// main loop
const int num_kv_iters = len_kv / BLOCK_KV;
for (int kv_idx = 0; kv_idx < num_kv_iters; kv_idx++) {
// accumulator for the 1st MMA. reset to zeros
float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4] = {}; // act as C/D in MMA
// load K global->shared->registers [BLOCK_KV, DIM]
// similar to loading Q, except we use ldmatrix_x2()
...
// 1st MMA: S = Q @ K.T
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++)
mma_m16n8k16(Q_rmem[mma_id_q][mma_id_d],
K_rmem[mma_id_kv][mma_id_d],
S_rmem[mma_id_q][mma_id_kv]);
// online softmax. we will touch on this later
// also pack S_rmem to P_rmem for the 2nd MMA
...
// load V global->shared->registers [BLOCK_KV, DIM]
// similar to loading K, except we use ldmatrix_x2_trans()
...
// 2nd MMA: O += P @ V
// similar to the 1st MMA
...
// increment pointer to the next KV block
K += BLOCK_KV * DIM;
V += BLOCK_KV * DIM;
}
// write output
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_N; mma_id_d++) {
const int row = warp_id * WARP_Q + mma_id_q * MMA_M + (lane_id / 4);
const int col = mma_id_d * MMA_N + (lane_id % 4) * 2;
float *regs = O_rmem[mma_id_q][mma_id_d];
reinterpret_cast<nv_bfloat162 *>(O + (row + 0) * DIM + col)[0] = __float22bfloat162_rn({regs[0], regs[1]});
reinterpret_cast<nv_bfloat162 *>(O + (row + 8) * DIM + col)[0] = __float22bfloat162_rn({regs[2], regs[3]});
}
}
// kernel launcher
void attention_v1(
const nv_bfloat16 *Q, // [bs, len_q, DIM]
const nv_bfloat16 *K, // [bs, len_kv, DIM]
const nv_bfloat16 *V, // [bs, len_kv, DIM]
nv_bfloat16 *O, // [bs, len_q, DIM]
int bs,
int len_q,
int len_kv) {
// 1 threadblock for each BLOCK_Q
const int num_blocks = bs * cdiv(len_q, BLOCK_Q);
// Q overlap with K+V.
const int smem_size = max(BLOCK_Q, BLOCK_KV * 2) * DIM * sizeof(nv_bfloat16);
// use dynamic shared memory so we can allocate more than 48kb if needed.
if (smem_size > 48'000)
CUDA_CHECK(cudaFuncSetAttribute(kernel, cudaFuncAttributeMaxDynamicSharedMemorySize, smem_size));
attention_v1_kernel<<<num_blocks, TB_SIZE, smem_size>>>(Q, K, V, O, bs, len_q, len_kv);
CUDA_CHECK(cudaGetLastError());
}constexpr int BLOCK_Q = 128;
constexpr int BLOCK_KV = 64;
constexpr int DIM = 128;
constexpr int NUM_WARPS = 4;
constexpr int TB_SIZE = NUM_WARPS * 32;
// mma.m16n8k16
constexpr int MMA_M = 16;
constexpr int MMA_N = 8;
constexpr int MMA_K = 16;
__global__
void attention_v1_kernel(
const nv_bfloat16 *Q, // [bs, len_q, DIM]
const nv_bfloat16 *K, // [bs, len_kv, DIM]
const nv_bfloat16 *V, // [bs, len_kv, DIM]
nv_bfloat16 *O, // [bs, len_q, DIM]
int bs,
int len_q,
int len_kv) {
// basic setup
const int tid = threadIdx.x;
const int warp_id = tid / 32;
const int lane_id = tid % 32;
// increment Q, K, V, O based on blockIdx.x
...
// set up shared memory
// Q_smem is overlapped with (K_smem + V_smem), since we only use Q_smem once
extern __shared__ uint8_t smem[];
const uint32_t Q_smem = __cvta_generic_to_shared(smem);
const uint32_t K_smem = Q_smem;
const uint32_t V_smem = K_smem + BLOCK_KV * DIM * sizeof(nv_bfloat16);
// FA2: shard BLOCK_Q among warps
constexpr int WARP_Q = BLOCK_Q / NUM_WARPS;
// set up register memory
uint32_t Q_rmem[WARP_Q / MMA_M][DIM / MMA_K][4]; // act as A in MMA
uint32_t K_rmem[BLOCK_KV / MMA_N][DIM / MMA_K][2]; // act as B in MMA
uint32_t P_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_K][4]; // act as A in MMA
uint32_t V_rmem[BLOCK_KV / MMA_K][DIM / MMA_N][2]; // act as B in MMA
float O_rmem[WARP_Q / MMA_M][DIM / MMA_N][4]; // act as C/D in MMA
// Q global->shared [BLOCK_Q, DIM]
global_to_shared<BLOCK_Q, DIM, TB_SIZE>(Q_smem, Q, DIM, tid);
asm volatile("cp.async.commit_group;");
asm volatile("cp.async.wait_all;");
__syncthreads();
// Q shared->register. select the correct warp tile
// Q stays in registers throughout the kernel's lifetime
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
const int row = warp_id * WARP_Q + mma_id_q * MMA_M + (lane_id % 16);
const int col = mma_id_d * MMA_K + (lane_id / 16 * 8);
const uint32_t addr = Q_smem + (row * DIM + col) * sizeof(nv_bfloat16);
ldmatrix_x4(Q_rmem[mma_id_q][mma_id_d], addr);
}
__syncthreads();
// main loop
const int num_kv_iters = len_kv / BLOCK_KV;
for (int kv_idx = 0; kv_idx < num_kv_iters; kv_idx++) {
// accumulator for the 1st MMA. reset to zeros
float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4] = {}; // act as C/D in MMA
// load K global->shared->registers [BLOCK_KV, DIM]
// similar to loading Q, except we use ldmatrix_x2()
...
// 1st MMA: S = Q @ K.T
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++)
mma_m16n8k16(Q_rmem[mma_id_q][mma_id_d],
K_rmem[mma_id_kv][mma_id_d],
S_rmem[mma_id_q][mma_id_kv]);
// online softmax. we will touch on this later
// also pack S_rmem to P_rmem for the 2nd MMA
...
// load V global->shared->registers [BLOCK_KV, DIM]
// similar to loading K, except we use ldmatrix_x2_trans()
...
// 2nd MMA: O += P @ V
// similar to the 1st MMA
...
// increment pointer to the next KV block
K += BLOCK_KV * DIM;
V += BLOCK_KV * DIM;
}
// write output
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_N; mma_id_d++) {
const int row = warp_id * WARP_Q + mma_id_q * MMA_M + (lane_id / 4);
const int col = mma_id_d * MMA_N + (lane_id % 4) * 2;
float *regs = O_rmem[mma_id_q][mma_id_d];
reinterpret_cast<nv_bfloat162 *>(O + (row + 0) * DIM + col)[0] = __float22bfloat162_rn({regs[0], regs[1]});
reinterpret_cast<nv_bfloat162 *>(O + (row + 8) * DIM + col)[0] = __float22bfloat162_rn({regs[2], regs[3]});
}
}
// kernel launcher
void attention_v1(
const nv_bfloat16 *Q, // [bs, len_q, DIM]
const nv_bfloat16 *K, // [bs, len_kv, DIM]
const nv_bfloat16 *V, // [bs, len_kv, DIM]
nv_bfloat16 *O, // [bs, len_q, DIM]
int bs,
int len_q,
int len_kv) {
// 1 threadblock for each BLOCK_Q
const int num_blocks = bs * cdiv(len_q, BLOCK_Q);
// Q overlap with K+V.
const int smem_size = max(BLOCK_Q, BLOCK_KV * 2) * DIM * sizeof(nv_bfloat16);
// use dynamic shared memory so we can allocate more than 48kb if needed.
if (smem_size > 48'000)
CUDA_CHECK(cudaFuncSetAttribute(kernel, cudaFuncAttributeMaxDynamicSharedMemorySize, smem_size));
attention_v1_kernel<<<num_blocks, TB_SIZE, smem_size>>>(Q, K, V, O, bs, len_q, len_kv);
CUDA_CHECK(cudaGetLastError());
}现在,让我们处理在线 softmax。
在线 softmax - 理论¶
对于原始解释,你可以参考softmax 的在线归一化器计算 和 Flash Attention 2 论文。
我们有 softmax 的以下数学定义。对于每行长度为
是最大减法以提高数值稳定性( 如果其输入很大,很容易爆炸)。让我们提取分母归一化器并将整行写成一个向量。
在我们的第二个矩阵乘法 O += P @ V 中,P(softmax 输出)的每一行与 V 的相应列进行点积。
额外的点积是塞翁失马——我们不再需要一行中的单个元素来获得最终结果。这使得 Flash Attention 能够一次性计算注意力。为了更清楚地看到这一点,让我们考虑在线计算期间添加新元素的迭代过程。
我在这里滥用了符号,但我希望传达这个想法。当我们添加一个新元素
查看归一化器(分母)
这个方程意味着我们只需要 在添加 之前。 相同的逻辑可以应用于与 V 的点积(未归一化输出)。这是在线 softmax 和 Flash Attention 的关键思想。
定义注意力状态
其中 是迄今为止看到的元素的最大值, 是未归一化的输出, 是归一化器。我们需要 来计算如上所示的重新缩放因子。
你可以说服自己,更新注意力状态是一个结合性操作——元素用于更新注意力状态的顺序无关紧要。
这种结合性属性使得诸如Flash Decoding(注意力的 split-K 版本)成为可能。
在线 softmax - 实现¶
我们现在可以在我们的高层级 Python 实现中填补在线 softmax 的空白。
# attention state
m = torch.zeros(BLOCK_Q)
tile_O = torch.zeros(BLOCK_Q, DIM)
sumexp = torch.zeros(BLOCK_Q)
for _ in range(Lk // BLOCK_KV):
# 1st MMA
tile_S = tile_Q @ tile_K.T # [BLOCK_Q, BLOCK_KV]
tile_S = tile_S * scale
# online softmax
tile_max = tile_S.amax(dim=-1) # [BLOCK_Q]
new_m = torch.maximum(m, tile_max)
tile_P = torch.exp(tile_S - new_m.unsqueeze(-1))
# rescale
scale = torch.exp(m - new_m)
tile_O *= scale.unsqueeze(-1)
sumexp = sumexp * scale + tile_P.sum(dim=-1)
m = new_m # save new max
# 2nd MMA
tile_O += tile_P @ tile_V # [BLOCK_Q, DIM]
# apply normalization
tile_O /= sumexp.unsqueeze(-1)# attention state
m = torch.zeros(BLOCK_Q)
tile_O = torch.zeros(BLOCK_Q, DIM)
sumexp = torch.zeros(BLOCK_Q)
for _ in range(Lk // BLOCK_KV):
# 1st MMA
tile_S = tile_Q @ tile_K.T # [BLOCK_Q, BLOCK_KV]
tile_S = tile_S * scale
# online softmax
tile_max = tile_S.amax(dim=-1) # [BLOCK_Q]
new_m = torch.maximum(m, tile_max)
tile_P = torch.exp(tile_S - new_m.unsqueeze(-1))
# rescale
scale = torch.exp(m - new_m)
tile_O *= scale.unsqueeze(-1)
sumexp = sumexp * scale + tile_P.sum(dim=-1)
m = new_m # save new max
# 2nd MMA
tile_O += tile_P @ tile_V # [BLOCK_Q, DIM]
# apply normalization
tile_O /= sumexp.unsqueeze(-1)行最大值¶
当将其转换为 CUDA C++ 时,最棘手的部分是理解 MMA 布局。让我们从 tile_S 开始。
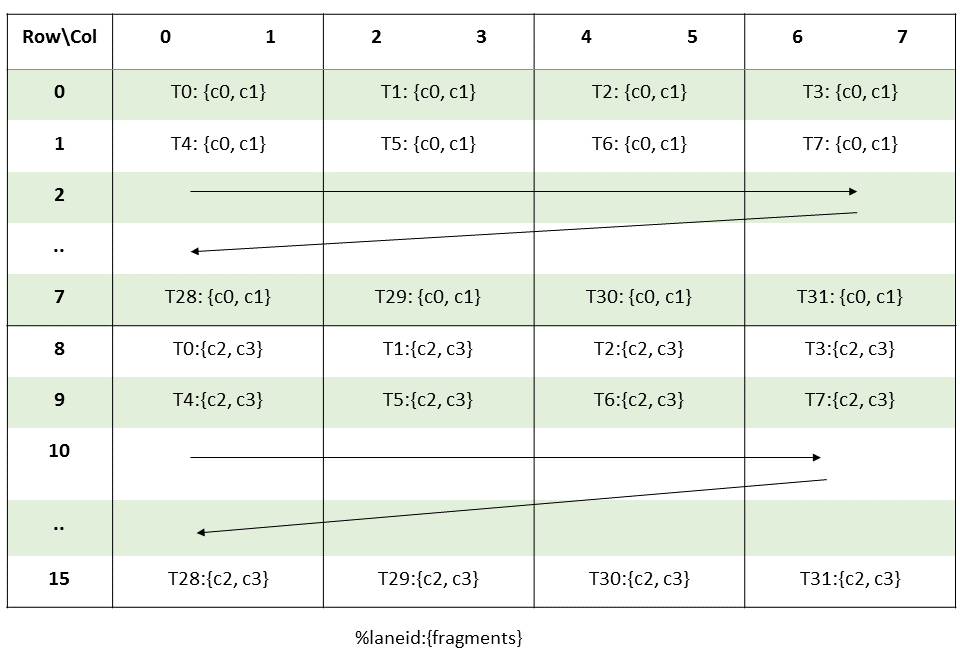
MMA m16n8k16 输出的线程和寄存器布局。来源:NVIDIA PTX 文档。
Softmax 缩放对所有元素应用相同的缩放,所以这很简单。接下来,我们需要计算当前 tile 的行最大值。记住我们为 tile_S 这样分配寄存器。
float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4];float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4];4 意味着 c0,c1,c2,c3 在上图中,即每个线程持有来自 2 行的 2 个连续元素。要在行内(MMA 输出 tile)进行归约,我们对线程持有的 2 个连续元素进行归约,然后在 4 个线程的组内进行归约,即 T0-T3、T4-T7 等等。然而,行归约实际上是在整个 tile_S 内进行的,因此我们还需要循环 BLOCK_KV / MMA_N 的 S_rmem。这可以与线程级归约结合,在 4 线程归约之前进行。
在 MMA 输出上执行行归约。
// initial attention state
float rowmax[WARP_Q / MMA_M][2];
float rowsumexp[WARP_Q / MMA_M][2] = {};
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++) {
rowmax[mma_id_q][0] = -FLT_MAX;
rowmax[mma_id_q][1] = -FLT_MAX;
}
// main loop
const int num_kv_iters = len_kv / BLOCK_KV;
for (int kv_idx = 0; kv_idx < num_kv_iters; kv_idx++) {
// tile_S = tile_Q @ tile_K.T
S_rmem[][] = ...
// loop over rows
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++) {
// apply softmax scale
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int reg_id = 0; reg_id < 4; reg_id++)
S_rmem[mma_id_q][mma_id_kv][reg_id] *= softmax_scale;
// rowmax
float this_rowmax[2] = {-FLT_MAX, -FLT_MAX};
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++) {
float *regs = S_rmem[mma_id_q][mma_id_kv];
this_rowmax[0] = max(this_rowmax[0], max(regs[0], regs[1])); // c0 and c1
this_rowmax[1] = max(this_rowmax[1], max(regs[2], regs[3])); // c2 and c3
}
// butterfly reduction within 4 threads
this_rowmax[0] = max(this_rowmax[0], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[0], 1));
this_rowmax[0] = max(this_rowmax[0], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[0], 2));
this_rowmax[1] = max(this_rowmax[1], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[1], 1));
this_rowmax[1] = max(this_rowmax[1], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[1], 2));
}
...
}// initial attention state
float rowmax[WARP_Q / MMA_M][2];
float rowsumexp[WARP_Q / MMA_M][2] = {};
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++) {
rowmax[mma_id_q][0] = -FLT_MAX;
rowmax[mma_id_q][1] = -FLT_MAX;
}
// main loop
const int num_kv_iters = len_kv / BLOCK_KV;
for (int kv_idx = 0; kv_idx < num_kv_iters; kv_idx++) {
// tile_S = tile_Q @ tile_K.T
S_rmem[][] = ...
// loop over rows
for (int mma_id_q = 0; mma_id_q < WARP_Q / MMA_M; mma_id_q++) {
// apply softmax scale
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int reg_id = 0; reg_id < 4; reg_id++)
S_rmem[mma_id_q][mma_id_kv][reg_id] *= softmax_scale;
// rowmax
float this_rowmax[2] = {-FLT_MAX, -FLT_MAX};
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++) {
float *regs = S_rmem[mma_id_q][mma_id_kv];
this_rowmax[0] = max(this_rowmax[0], max(regs[0], regs[1])); // c0 and c1
this_rowmax[1] = max(this_rowmax[1], max(regs[2], regs[3])); // c2 and c3
}
// butterfly reduction within 4 threads
this_rowmax[0] = max(this_rowmax[0], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[0], 1));
this_rowmax[0] = max(this_rowmax[0], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[0], 2));
this_rowmax[1] = max(this_rowmax[1], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[1], 1));
this_rowmax[1] = max(this_rowmax[1], __shfl_xor_sync(0xFFFF'FFFF, this_rowmax[1], 2));
}
...
}在典型的归约内核中,当只剩下 32 个活动线程时,我们可以使用 warp shuffle __shfl_down_sync() 将数据从较高通道复制到较低通道,最终结果存储在线程 0 中。在这种情况下,由于我们需要最大值在组内的 4 个线程之间共享(用于后续的最大减法),我们可以使用 __shfl_xor_sync() 以避免额外的广播步骤。
使用__shfl_xor_sync() 在 4 个线程内进行蝶形归约。
重新缩放¶
有了新 tile 的行最大值,我们可以计算(未归一化)输出的重新缩放因子以及归一化器(每行的 sumexp)。
// new rowmax
this_rowmax[0] = max(this_rowmax[0], rowmax[mma_id_q][0]);
this_rowmax[1] = max(this_rowmax[1], rowmax[mma_id_q][1]);
// rescale for previous O
float rescale[2];
rescale[0] = __expf(rowmax[mma_id_q][0] - this_rowmax[0]);
rescale[1] = __expf(rowmax[mma_id_q][1] - this_rowmax[1]);
for (int mma_id_d = 0; mma_id_d < DIM / MMA_N; mma_id_d++) {
O_rmem[mma_id_q][mma_id_d][0] *= rescale[0];
O_rmem[mma_id_q][mma_id_d][1] *= rescale[0];
O_rmem[mma_id_q][mma_id_d][2] *= rescale[1];
O_rmem[mma_id_q][mma_id_d][3] *= rescale[1];
}
// save new rowmax
rowmax[mma_id_q][0] = this_rowmax[0];
rowmax[mma_id_q][1] = this_rowmax[1];// new rowmax
this_rowmax[0] = max(this_rowmax[0], rowmax[mma_id_q][0]);
this_rowmax[1] = max(this_rowmax[1], rowmax[mma_id_q][1]);
// rescale for previous O
float rescale[2];
rescale[0] = __expf(rowmax[mma_id_q][0] - this_rowmax[0]);
rescale[1] = __expf(rowmax[mma_id_q][1] - this_rowmax[1]);
for (int mma_id_d = 0; mma_id_d < DIM / MMA_N; mma_id_d++) {
O_rmem[mma_id_q][mma_id_d][0] *= rescale[0];
O_rmem[mma_id_q][mma_id_d][1] *= rescale[0];
O_rmem[mma_id_q][mma_id_d][2] *= rescale[1];
O_rmem[mma_id_q][mma_id_d][3] *= rescale[1];
}
// save new rowmax
rowmax[mma_id_q][0] = this_rowmax[0];
rowmax[mma_id_q][1] = this_rowmax[1];我们不重新缩放 rowsumexp,因为我们希望稍后将其与新 sumexp 项的加法融合,即 FMA(融合乘加)。我们不能将乘法与 MMA 融合,因此我们需要对 O_rmem 进行单独的乘法。
打包到 BF16 并计算行求和 exp¶
对于下一部分,我们将再次循环遍历行维度(BLOCK_KV / MMA_N),计算并打包 tile_S 到 tile_P,同时计算行求和 exp(在线 softmax 的一部分)。
float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4] // m16n8
uint32_t P_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_K][4]; // m16k16float S_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_N][4] // m16n8
uint32_t P_rmem[WARP_Q / MMA_M][BLOCK_KV / MMA_K][4]; // m16k16在 PTX 文档中查找 MMA 乘数 A 和输出 C/D 的线程/寄存器布局。幸运的是,它们是相同的。
乘数 A 的左半部分与累加器具有相同的布局。来源:NVIDIA PTX 文档
这意味着对于所有线程,S_rmem 中的每 2 个浮点数可以作为 BF16x2 打包到单个 32 位寄存器中,并存储到 P_rmem 中,而无需改变布局。
我们的在线 softmax 最后部分的代码如下。
// rowsumexp
float this_rowsumexp[2] = {};
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++) {
float *regs = S_rmem[mma_id_q][mma_id_kv];
regs[0] = __expf(regs[0] - rowmax[mma_id_q][0]); // c0
regs[1] = __expf(regs[1] - rowmax[mma_id_q][0]); // c1
regs[2] = __expf(regs[2] - rowmax[mma_id_q][1]); // c2
regs[3] = __expf(regs[3] - rowmax[mma_id_q][1]); // c3
this_rowsumexp[0] += regs[0] + regs[1];
this_rowsumexp[1] += regs[2] + regs[3];
// pack to P registers for next MMA
// we need to change from m16n8 to m16k16
// each iteration of this loop packs half of m16k16
nv_bfloat162 *this_P_rmem = reinterpret_cast<nv_bfloat162 *>(P_rmem[mma_id_q][mma_id_kv / 2]);
this_P_rmem[(mma_id_kv % 2) * 2] = __float22bfloat162_rn({regs[0], regs[1]}); // top row
this_P_rmem[(mma_id_kv % 2) * 2 + 1] = __float22bfloat162_rn({regs[2], regs[3]}); // bottom row
}
// butterfly reduction on this_rowsumexp[2]
...
// accumulate to total rowsumexp using FMA
rowsumexp[mma_id_q][0] = rowsumexp[mma_id_q][0] * rescale[0] + this_rowsumexp[0];
rowsumexp[mma_id_q][1] = rowsumexp[mma_id_q][1] * rescale[1] + this_rowsumexp[1];// rowsumexp
float this_rowsumexp[2] = {};
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++) {
float *regs = S_rmem[mma_id_q][mma_id_kv];
regs[0] = __expf(regs[0] - rowmax[mma_id_q][0]); // c0
regs[1] = __expf(regs[1] - rowmax[mma_id_q][0]); // c1
regs[2] = __expf(regs[2] - rowmax[mma_id_q][1]); // c2
regs[3] = __expf(regs[3] - rowmax[mma_id_q][1]); // c3
this_rowsumexp[0] += regs[0] + regs[1];
this_rowsumexp[1] += regs[2] + regs[3];
// pack to P registers for next MMA
// we need to change from m16n8 to m16k16
// each iteration of this loop packs half of m16k16
nv_bfloat162 *this_P_rmem = reinterpret_cast<nv_bfloat162 *>(P_rmem[mma_id_q][mma_id_kv / 2]);
this_P_rmem[(mma_id_kv % 2) * 2] = __float22bfloat162_rn({regs[0], regs[1]}); // top row
this_P_rmem[(mma_id_kv % 2) * 2 + 1] = __float22bfloat162_rn({regs[2], regs[3]}); // bottom row
}
// butterfly reduction on this_rowsumexp[2]
...
// accumulate to total rowsumexp using FMA
rowsumexp[mma_id_q][0] = rowsumexp[mma_id_q][0] * rescale[0] + this_rowsumexp[0];
rowsumexp[mma_id_q][1] = rowsumexp[mma_id_q][1] * rescale[1] + this_rowsumexp[1];之后是第二个 MMA:加载 V,然后计算 tile_O += tile_P @ tile_V。这完成了我们的第一个版本。
你可以在 attention_v1.cu 找到版本 1 的完整代码。
基准测试设置¶
哇,第一个版本的内容已经很丰富了。确实,我在版本 1 上花费了最多的时间,试图正确实现算法并消除所有错误。
无论如何,现在我们需要一个脚本来进行正确性检查和速度基准测试。我更喜欢用 Python 完成这些任务。正确性检查和速度基准测试通常在 test.py 和 benchmark.py 中分开,但我更喜欢将它们放在同一个脚本中。
attention.cpp:为我的注意力内核提供 PyTorch 绑定。
- main.py:正确性检查和速度基准测试。
对于正确性检查,我与 F.sdpa() 进行比较,默认情况下应该调度 Flash Attention 2(如果可用)。
def generate_input(*shape):
return torch.randn(shape).add(0.5).bfloat16().cuda()def generate_input(*shape):
return torch.randn(shape).add(0.5).bfloat16().cuda()对于速度基准测试,通常最好与(1)硬件的理论极限和(2)已知的良好实现进行比较。前者让我们知道还有多少改进空间,后者让我们了解与生产质量代码相比的情况。
要计算给定内核的 FLOPS,我们计算所需的浮点操作次数(FLOPs)并除以内核运行时间。可以在这里 找到我的 FLOPs 计数。
“已知的良好实现”是 F.sdpa() 的 FA2 和 CuDNN 后端,以及来自 flash-attn 库的 FA2。我认为最好在自定义 C++ 扩展内包装它们,这样它们就可以在同一个 Python 脚本中进行基准测试,就像我们的内核一样。请参阅 reference.cpp 和 reference.py 了解如何完成。flash-attn 库需要单独安装。
| Kernel | TFLOPS | % of SOL |
|---|---|---|
F.sdpa() (Flash Attention) | 186.73 | 89.13% |
F.sdpa() (CuDNN) | 203.61 | 97.19% |
flash-attn | 190.58 | 90.97% |
| v1 (basic) | 142.87 | 68.20% |
第一个版本看起来还不错,但我们还有一些改进空间。没关系,因为我们有几个版本要介绍。
Profiling¶
在进入下一个版本之前,我想谈谈分析工具。我认为最好尽早熟悉分析工具——这样可以更快地识别性能瓶颈。
Nsight Compute 可以在 macOS 上运行,通过 SSH 访问另一台装有 NVIDIA GPU 的机器,这正是我的设置。请参阅 Nsight Compute 的远程分析文档。
要启用源代码检查功能,请记住将 -lineinfo 传递给 NVCC(请参阅这里)。
版本 2 - Shared memory swizzling¶
让我们使用 Nsight Compute 进行分析,并查看 Warp State Statistics 部分。
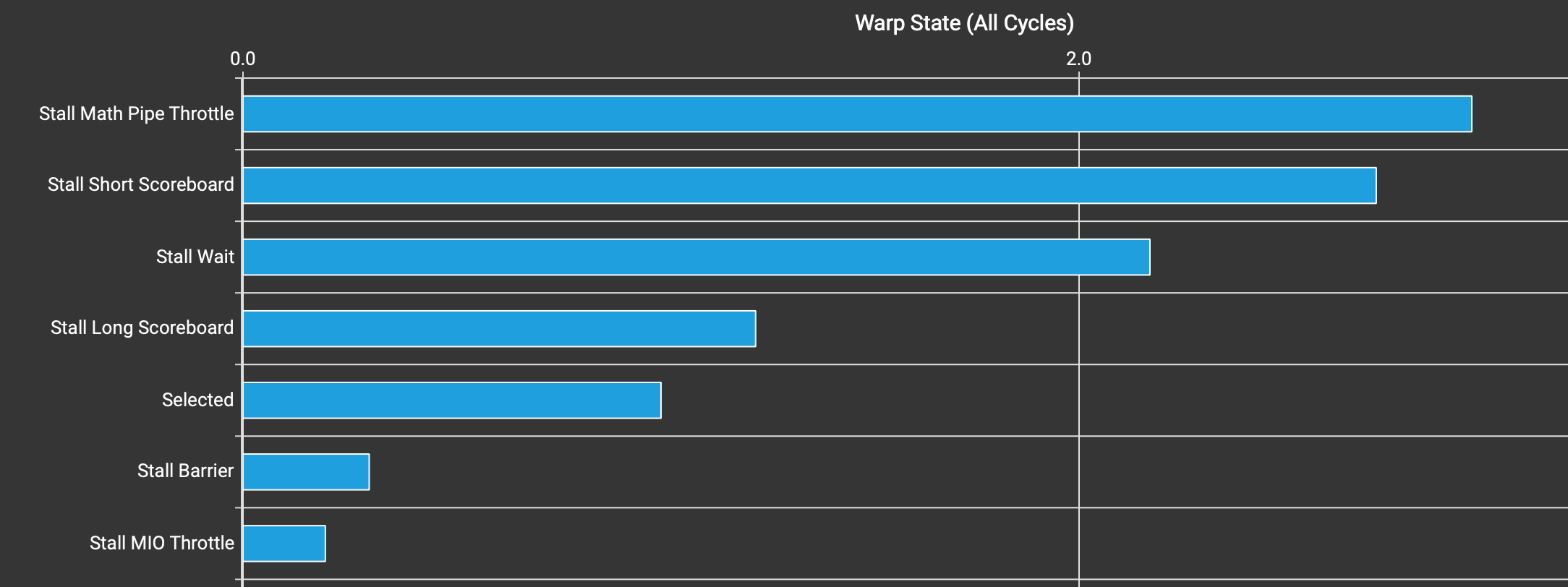
内核 v1 的 warp 状态统计。
Stall Math Pipe Throttle 最高是好事——这意味着 warp 忙于数学运算,必须等待/停顿以等待数学运算延迟。查看前 2 个停顿原因(Stall Math Pipe Throttle 和 Stall Long Scoreboard),我们似乎确实在最大化利用计算单元。
我们可以通过查看 Memory Workload Analysis 来再次确认这一点,它揭示了几个问题。

内核 v1 的内存分析。
L1TEX Global Store Access Pattern 来自存储输出,因为这是我们唯一的全局写入。这并不重要,因为当 len_kv 很大时,循环遍历 KV 序列长度的运行时间应该占主导地位。
- L1TEX Local Load/Store Access Pattern 是由于寄存器溢出。由于是寄存器溢出,一次只溢出和重新加载 1 个元素是正常的。减少
BLOCK_Q(这样我们使用更少的寄存器来保存累加器)可以解决这个问题,但我的手动调整表明,一些溢出实际上更快。 - Shared Load Bank Conflicts 正是我们要寻找的——导致 “Stall Short Scoreboard” 的 bank 冲突。
NVIDIA GPU 的 shared memory 由 32 个 memory bank 支持。连续的 4 字节内存地址分配给连续的 memory bank。当我们使用 ldmatrix 从 shared 加载数据到 register memory 时,这会带来问题。虽然在任何文档中都没有明确说明,但 ldmatrix.x2 和 ldmatrix.x4 每次操作一个 8x8 的 tile。这很好,因为它简化了我们的分析:我们只需要考虑加载一个 8x8 tile 的情况。
考虑共享内存中一个形状为 8x64、数据类型为 BF16 的 2D 图块。
共享内存中 8x64 BF16 图块的内存 bank 分布。
从上图可知,当我们加载 8x8 ldmatrix 图块时,相同的 4 个 bank 0-3 服务所有 32 个线程,导致 8 路 bank 冲突。我不确定为什么 Nsight Compute 如上所示报告 16 路 bank 冲突。我尝试查找 matmul blogposts with swizzling 和 NVIDIA forum threads,并发现另一种检查 bank 冲突的方法是转到 Nsight Compute 的 Source 选项卡并检查 L1 Wavefronts Shared 和 L1 Wavefronts Shared Ideal(我必须手动启用这两列,因为默认情况下它们没有显示)。

内核 v1 中 ldmatrix 的实际和理想 L1 Wavefronts Shared。
的比率Actual / Ideal为 8,符合我们关于 8 路 bank 冲突的假设。我仍然不确定为什么这个值与Details选项卡中的值存在差异。
无论如何,这个问题有两种标准解决方案
- Pad shared memory。由于
ldmatrix的对齐要求,我们只能将宽度填充 16 字节,相当于 4 个 bank。这意味着当我们转到下一行时,内存 bank 会偏移 4,从而避免 bank 冲突。在许多情况下,这已经足够好了。然而,这通常相当浪费,因为我们没有利用填充的存储空间。 - Swizzle shared memory address。这是黑魔法:你用一些魔术数字对共享内存地址进行 XOR 运算,然后 bank 冲突突然消失了!
让我们详细说明第二种方法。我不够聪明发明这个技巧,但至少我希望我能给出一些关于为什么它合理的提示。我们使用 XOR 是因为这个操作很好地置换数据——在给定固定第二个输入的情况下,输入和输出之间存在一一映射。我们遇到 bank 冲突是因为当我们移动到下一行时,我们再次命中相同的内存 bank -> 我们可以使用这个行索引来置换地址。
具体来说,如果我们查看原始行地址:
- Bits 0-3由于 16 字节对齐约束始终为零。
- Bits 2-6决定 bank 索引。我们只需要关心 bits 4-6,因为低位始终为零(由于对齐)。
- 行步长决定了当我们移动到下一行时哪些位会递增(根据定义)。如果我们的 2D 图块宽度为 64 个 BF16 元素,行步长为 128 字节。转到下一行将递增 bit 7,留下bits 0-6 unchanged(但我们不关心 bits 0-3)。
- 因此,我们可以将行地址的bits 4-6与行索引的bits 0-2进行 XOR 运算,这保证每行都会改变。
如果图块宽度不同,例如 32 BF16,我们可以进行相同的推理。还要注意行索引编码在行地址内,因此我们只需要行地址和行步长来进行 swizzling。
// NOTE: stride in bytes
template <int STRIDE>
__device__
uint32_t swizzle(uint32_t index) {
// no need swizzling
if constexpr (STRIDE == 16)
return index;
uint32_t row_idx = (index / STRIDE) % 8;
uint32_t bits_to_xor = row_idx / max(64 / STRIDE, 1);
return index ^ (bits_to_xor << 4);
}// NOTE: stride in bytes
template <int STRIDE>
__device__
uint32_t swizzle(uint32_t index) {
// no need swizzling
if constexpr (STRIDE == 16)
return index;
uint32_t row_idx = (index / STRIDE) % 8;
uint32_t bits_to_xor = row_idx / max(64 / STRIDE, 1);
return index ^ (bits_to_xor << 4);
}要启用此 swizzling,我们需要将其添加到 cp.async(写入共享内存)和 ldmatrix(从共享内存读取)调用中。
// for cp.async
- const uint32_t dst_addr = dst + (row * WIDTH + col) * sizeof(nv_bfloat16);
+ const uint32_t dst_addr = swizzle<WIDTH * sizeof(nv_bfloat16)>(dst + (row * WIDTH + col) * sizeof(nv_bfloat16));
asm volatile("cp.async.cg.shared.global [%0], [%1], 16;" :: "r"(dst_addr), "l"(src_addr));
// for ldmatrix
- ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], addr);
+ ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], swizzle<DIM * sizeof(nv_bfloat16)>(addr));// for cp.async
- const uint32_t dst_addr = dst + (row * WIDTH + col) * sizeof(nv_bfloat16);
+ const uint32_t dst_addr = swizzle<WIDTH * sizeof(nv_bfloat16)>(dst + (row * WIDTH + col) * sizeof(nv_bfloat16));
asm volatile("cp.async.cg.shared.global [%0], [%1], 16;" :: "r"(dst_addr), "l"(src_addr));
// for ldmatrix
- ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], addr);
+ ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], swizzle<DIM * sizeof(nv_bfloat16)>(addr));由于这是 matmul 内核中的标准优化,我还为 ldmatrix 添加了一个小优化。我在主循环外预计算行地址和 swizzling,以便在热循环中减少工作。当我们在 warp 图块内迭代 MMA 图块时,需要递增地址。然而,swizzling 是 XOR 操作,我们不能简单地将 XOR 与加法交换,即 (a + b) ^ c != (a ^ c) + b。注意,如果基地址 a 有某种对齐,加法就变成了 XOR!即 100 + 001 == 100 ^ 001。因此,当递增 ldmatrix 的输入地址时,我们将其与列偏移进行 XOR 运算,而不是进行加法。行偏移会影响高于 swizzled 位的位,因此我们可以对其保持加法。
// K shared->registers
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
// swizzle(addr + offset) = swizzle(addr) XOR offset
uint32_t addr = K_smem_thread;
addr += mma_id_kv * MMA_N * DIM * sizeof(nv_bfloat16); // row
addr ^= mma_id_d * MMA_K * sizeof(nv_bfloat16); // col
ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], addr);
}// K shared->registers
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d++) {
// swizzle(addr + offset) = swizzle(addr) XOR offset
uint32_t addr = K_smem_thread;
addr += mma_id_kv * MMA_N * DIM * sizeof(nv_bfloat16); // row
addr ^= mma_id_d * MMA_K * sizeof(nv_bfloat16); // col
ldmatrix_x2(K_rmem[mma_id_kv][mma_id_d], addr);
}版本 2:attention_v2.cu。
我们可以用 Nsight Compute 验证不再有 bank 冲突。基准测试结果显示有显著的性能提升(我总是为新版本的内核重新调整 BLOCK_Q 和 BLOCK_KV)。
| Kernel | TFLOPS | % of SOL |
|---|---|---|
| v1 (basic) | 142.87 | 68.20% |
| v2 (shared memory swizzling) | 181.11 | 86.45% |
版本 3 - 2 级流水线¶
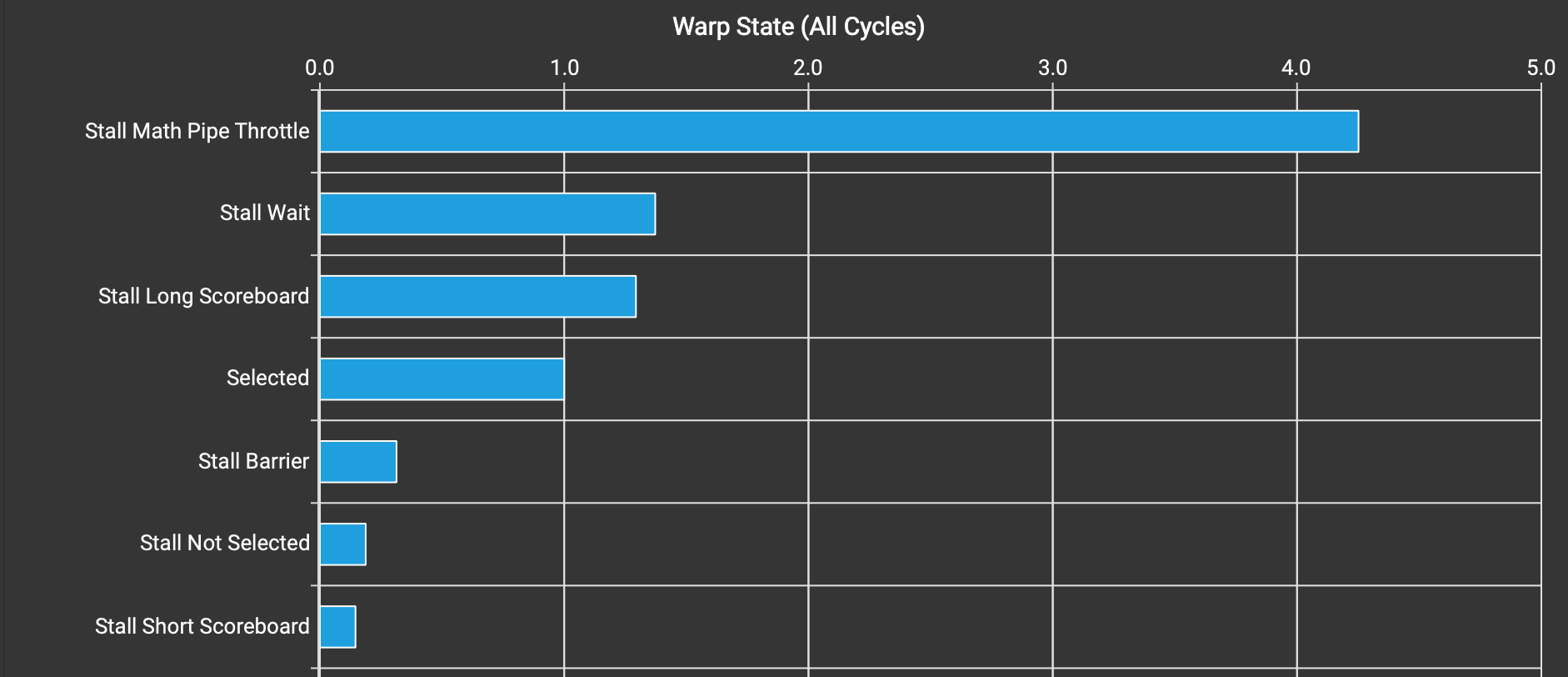
内核 v2 的 Warp 状态统计。
Stall Short Scoreboard不再是问题,因为我们已经通过 swizzling 处理了它。现在的问题是:
- Stall Wait(
stalled_wait在 Nsight Compute 文档中):“等待固定延迟的执行依赖”,似乎不是大问题。 - Stall Long Scoreboard(
stalled_long_scoreboard在 Nsight Compute 文档中):通常意味着等待全局内存访问。
到目前为止,我们还没有将全局内存操作与计算操作(MMA)重叠。这意味着 Tensor Core 在等待全局->共享传输完成时处于空闲状态。这似乎是引入pipelining或double-buffering的合适时机:分配比需要更多的共享内存,以便我们可以在处理当前迭代时预取下一个迭代的数据。
- 技术上我们也可以流水线化共享->寄存器数据传输。这实际上在 CUTLASS 的Efficient GEMM doc 中提到。然而,我从未在我的 5090 上成功实现它。检查我当前代码生成的 SASS,我看到
LDSM(ldmatrix在 PTX 中)和HMMA(半精度mma在 PTX 中)之间存在交错,可能由编译器完成以实现类似的内存-计算重叠效果。
让我们讨论N-stage pipelining的更通用实现。这个NVIDIA blogpost 很好地解释了这个想法,但通常我不太喜欢使用 CUDA C++ API(考虑到 CUTLASS 也不使用,我认为直接使用 PTX 更有趣)。N-stage 意味着在任何时间点都有 N 个进行中的阶段。这将是我们在整个内循环中想要保持的invariance。
- 这与
num_stages中提到的triton.Config 用于自动调优的概念相同。 - 双缓冲是 N=2 的特殊情况。
num_stages = 4
# set up num_stages buffers
tile_K_buffers = torch.empty(num_stages, BLOCK_KV, DIM)
tile_V_buffers = torch.empty(num_stages, BLOCK_KV, DIM)
# initiate with (num_stages-1) prefetches
# this is async: the code continues before data loading finishes.
for stage_idx in range(num_stages-1):
tile_K_buffers[stage_idx] = load_K(stage_idx)
tile_V_buffers[stage_idx] = load_V(stage_idx)
for tile_KV_idx in range(Lk // BLOCK_KV):
# prefetch tile (num_stages-1) ahead
# now we have num_stages global->shared inflight.
# in practice, we need to guard against out of bounds memory access.
prefetch_idx = tile_KV_idx + num_stages - 1
tile_K_buffers[prefetch_idx % num_stages] = load_K(prefetch_idx)
tile_V_buffers[prefetch_idx % num_stages] = load_V(prefetch_idx)
# select the current tile
# we need a synchronization mechanism to make sure data loading
# for this tile has finished.
# this "consumes" the oldest global->shared inflight, and
# replaces it with a compute stage.
tile_K = tile_K_buffers[tile_KV_idx % num_stages]
tile_V = tile_V_buffers[tile_KV_idx % num_stages]
# compute attention as normal
...num_stages = 4
# set up num_stages buffers
tile_K_buffers = torch.empty(num_stages, BLOCK_KV, DIM)
tile_V_buffers = torch.empty(num_stages, BLOCK_KV, DIM)
# initiate with (num_stages-1) prefetches
# this is async: the code continues before data loading finishes.
for stage_idx in range(num_stages-1):
tile_K_buffers[stage_idx] = load_K(stage_idx)
tile_V_buffers[stage_idx] = load_V(stage_idx)
for tile_KV_idx in range(Lk // BLOCK_KV):
# prefetch tile (num_stages-1) ahead
# now we have num_stages global->shared inflight.
# in practice, we need to guard against out of bounds memory access.
prefetch_idx = tile_KV_idx + num_stages - 1
tile_K_buffers[prefetch_idx % num_stages] = load_K(prefetch_idx)
tile_V_buffers[prefetch_idx % num_stages] = load_V(prefetch_idx)
# select the current tile
# we need a synchronization mechanism to make sure data loading
# for this tile has finished.
# this "consumes" the oldest global->shared inflight, and
# replaces it with a compute stage.
tile_K = tile_K_buffers[tile_KV_idx % num_stages]
tile_V = tile_V_buffers[tile_KV_idx % num_stages]
# compute attention as normal
...NVIDIA 工程师/架构师赐予我们 cp.async.commit_group 和 cp.async.wait_group 来优雅地实现这一点。
cp.async.commit_group:一个cp.async组自然映射到流水线中的一个预取阶段。cp.async.wait_group N:意味着等待直到最多剩下 N 个进行中的组。如果我们执行cp.async.wait_group num_stages-1,这意味着我们等待直到最早的预取完成(记住,我们始终有num_stages个进行中的预取作为循环不变量)。
在我们实现注意力机制的情况下,有两个小的改动。
- 由于我们已经为 K 和 V 消耗了大量共享内存,且消费级 GPU 的共享内存大小通常适中,相比其服务器版本,我决定保持为 2 级流水线,这也使代码略微简化。
- 我们可以拆分 K 和 V 的预取,因为 V 的预取可以在第一次 MMA 之后延迟发出。第二个改动需要一些微调:每个 K 和 V 预取是独立的
cp.async组(以便我们可以独立等待它们)。
我从Mingfei Ma(PyTorch CPU 后端的维护者)那里学到的一个简洁编码风格是使用lambda 表达式 来编写预取代码。它带来两个好处:(1)保持相关代码靠近调用点,(2)使多次调用同一代码块非常清晰。
const int num_kv_iter = cdiv(len_kv, BLOCK_KV);
auto load_K = [&](int kv_id) {
// guard against out-of-bounds global read
if (kv_id < num_kv_iter) {
// select the shared buffer destination
const uint32_t dst = K_smem + (kv_id % 2) * (2 * BLOCK_KV * DIM * sizeof(nv_bfloat16));
global_to_shared_swizzle<BLOCK_KV, DIM, TB_SIZE>(dst, K, DIM, tid);
// load_K() will be in charge of incrementing global memory address
K += BLOCK_KV * DIM;
}
// we always commit a cp-async group regardless of whether there is a cp.async
// to maintain loop invariance.
asm volatile("cp.async.commit_group;");
};
auto load_V = ...;
// prefetch K and V
load_K(0);
load_V(0);
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
// prefetch K for the next iteration
// now we have 3 prefetches in flight: K-V-K
load_K(kv_id + 1);
// wait for prefetch of current K to finish and load K shared->registers
// now we have 2 prefetches in flight: V-K
asm volatile("cp.async.wait_group 2;");
__syncthreads();
...
// 1st MMA
...
// prefetch V for the next iteration
// now we have 3 prefetches in flight: V-K-V
load_V(kv_id + 1);
// online softmax
...
// wait for prefetch of current V to finish and load V shared->registers
// now we have 2 prefetches in flight: K-V
asm volatile("cp.async.wait_group 2;");
__syncthreads();
...
// 2nd MMA
...
}const int num_kv_iter = cdiv(len_kv, BLOCK_KV);
auto load_K = [&](int kv_id) {
// guard against out-of-bounds global read
if (kv_id < num_kv_iter) {
// select the shared buffer destination
const uint32_t dst = K_smem + (kv_id % 2) * (2 * BLOCK_KV * DIM * sizeof(nv_bfloat16));
global_to_shared_swizzle<BLOCK_KV, DIM, TB_SIZE>(dst, K, DIM, tid);
// load_K() will be in charge of incrementing global memory address
K += BLOCK_KV * DIM;
}
// we always commit a cp-async group regardless of whether there is a cp.async
// to maintain loop invariance.
asm volatile("cp.async.commit_group;");
};
auto load_V = ...;
// prefetch K and V
load_K(0);
load_V(0);
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
// prefetch K for the next iteration
// now we have 3 prefetches in flight: K-V-K
load_K(kv_id + 1);
// wait for prefetch of current K to finish and load K shared->registers
// now we have 2 prefetches in flight: V-K
asm volatile("cp.async.wait_group 2;");
__syncthreads();
...
// 1st MMA
...
// prefetch V for the next iteration
// now we have 3 prefetches in flight: V-K-V
load_V(kv_id + 1);
// online softmax
...
// wait for prefetch of current V to finish and load V shared->registers
// now we have 2 prefetches in flight: K-V
asm volatile("cp.async.wait_group 2;");
__syncthreads();
...
// 2nd MMA
...
}我实验了一下在循环中放置 load_K/V 和 cp.async.wait_group 的位置,发现上述放置方式产生了最佳性能。虽然最终这取决于编译器如何重新排列和交错不同指令,但上述放置方式是有道理的:将 load_V() 放在第一次 MMA 之后,以便当 K 数据在寄存器中时张量核心可以立即开始工作(而不是等待发出 V 的 cp.async),即保持张量核心忙碌;load_V() 放在在线 softmax 之前以保持内存引擎忙碌(而 CUDA 核心正在处理在线 softmax)。同样,最优放置也可能很大程度上取决于硬件,例如内存和计算的速度相对关系,不同的内存和计算单元是否可以同时工作……
版本 3:attention_v3.cu。
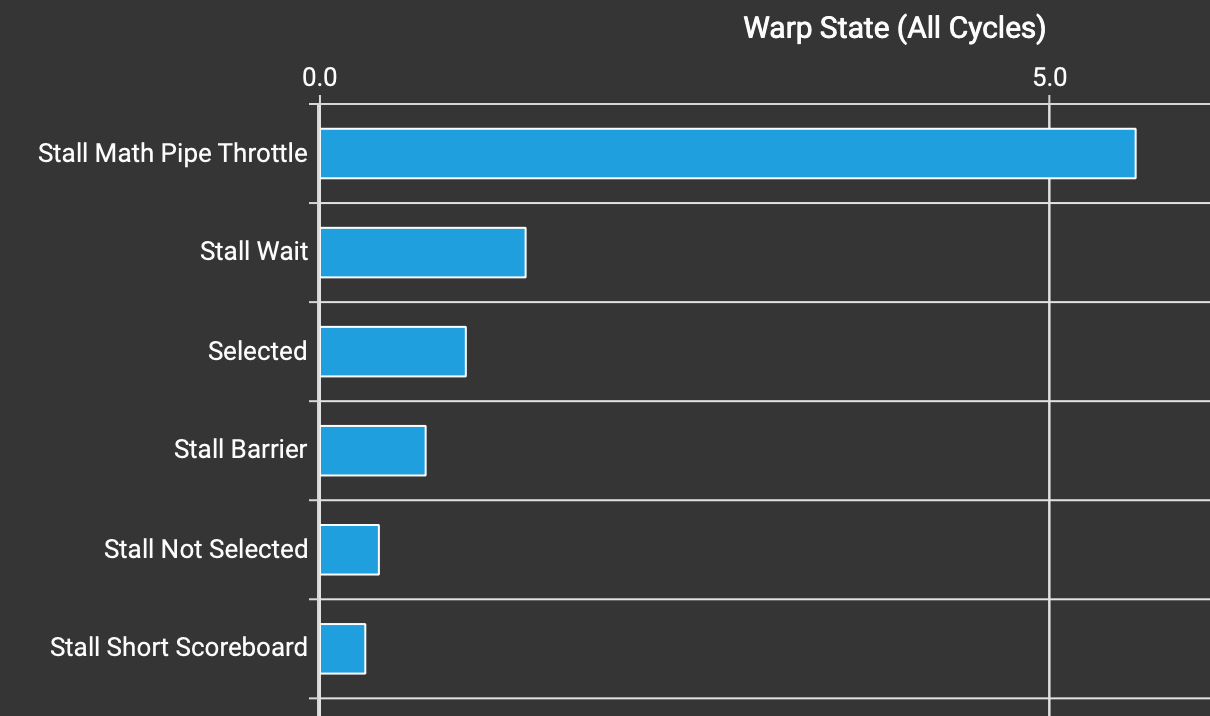
内核 v3 的 Warp 状态统计。
Stall Long Scoreboard 现在已从 Warp 状态统计中消失。我还必须将 BLOCK_KV 从 64 减少到 32,因为我们现在为 K 和 V 使用两个缓冲区,以便共享内存使用总量保持不变。
| 内核 | TFLOPS | % of SOL |
|---|---|---|
| v2(共享内存重排) | 181.11 | 86.45% |
| v3(2 级流水线) | 189.84 | 90.62% |
版本 4 - 对 K 和 V 使用 ldmatrix.x4¶
对于最后两个版本,我无法从性能分析数据中识别出任何优化机会(也许只是技能问题)。这些想法主要来自阅读随机资料和盯着内核看。
之前,我们使用 ldmatrix.x2 用于 K 和 V,因为它自然适合 n8k16 MMA tile。然而,既然我们无论如何都在处理更大的 tile,我们可以直接使用 ldmatrix.x4 来发出更少的指令。有两个选项:加载 n16k16 tile,或 n8k32 tile。
对乘数 B 使用 ldmatrix.x4 的可能选项。
一个选项比另一个更好吗?我们可以尝试从算术强度方面做一些分析。乍一看,n16k16 看起来是更好的选项:2 个 ldmatrix.x4(1 个用于 A 和 1 个用于 B)来执行 2 个 mma.m16n8k16;而 n8k32 选项需要 3 个 ldmatrix.x4(2 个用于 A 和 1 个用于 B)来执行 2 个 mma.m16n8k16。如果我们要为矩阵乘法内核实现这个想法,这个分析是有道理的。然而,在我们的情况下,乘数 A(查询)已经在寄存器中,因此我们只需要考虑乘数 B(键和值)的加载成本。这个认识表明两个选项应该是相同的。
你当然可以选择不同的模式来加载 K 和 V,但我希望至少这里提供的两个选项更有条理一些。要实现这个想法,关键是选择正确的 8x8 ldmatrix tile 的行地址。
{
// pre-compute ldmatrix address for K, using n8k32 option
// [8x8][8x8][8x8][8x8]
const int row_off = lane_id % 8;
const int col_off = lane_id / 8 * 8;
K_smem_thread = swizzle<DIM * sizeof(nv_bfloat16)>(K_smem + (row_off * DIM + col_off) * sizeof(nv_bfloat16));
}
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
...
// K shared->registers
// notice mma_id_d is incremented by 2
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d += 2) {
uint32_t addr = K_smem_thread + (kv_id % 2) * (2 * BLOCK_KV * DIM * sizeof(nv_bfloat16));
addr += mma_id_kv * MMA_N * DIM * sizeof(nv_bfloat16); // row
addr ^= mma_id_d * MMA_K * sizeof(nv_bfloat16); // col
ldmatrix_x4(K_rmem[mma_id_kv][mma_id_d], addr);
}
...
}{
// pre-compute ldmatrix address for K, using n8k32 option
// [8x8][8x8][8x8][8x8]
const int row_off = lane_id % 8;
const int col_off = lane_id / 8 * 8;
K_smem_thread = swizzle<DIM * sizeof(nv_bfloat16)>(K_smem + (row_off * DIM + col_off) * sizeof(nv_bfloat16));
}
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
...
// K shared->registers
// notice mma_id_d is incremented by 2
for (int mma_id_kv = 0; mma_id_kv < BLOCK_KV / MMA_N; mma_id_kv++)
for (int mma_id_d = 0; mma_id_d < DIM / MMA_K; mma_id_d += 2) {
uint32_t addr = K_smem_thread + (kv_id % 2) * (2 * BLOCK_KV * DIM * sizeof(nv_bfloat16));
addr += mma_id_kv * MMA_N * DIM * sizeof(nv_bfloat16); // row
addr ^= mma_id_d * MMA_K * sizeof(nv_bfloat16); // col
ldmatrix_x4(K_rmem[mma_id_kv][mma_id_d], addr);
}
...
}版本 4:attention_v4.cu。
| 内核 | TFLOPS | % of SOL |
|---|---|---|
| v3(2 级流水线) | 189.84 | 90.62% |
v4(ldmatrix.x4 用于 K 和 V) | 194.33 | 92.76% |
我对这个加速感到相当惊讶。这个版本唯一的区别是我们在主循环中使用了 2 倍更少的 ldmatrix 指令。然而,我们获得了显著的改进,接近 SOL。我猜是因为在新 GPU 中,张量核心和内存引擎非常快,调度和发出指令可能成为瓶颈!
版本 5 - 更好的流水线¶
在版本 3 中,我们为 K 和 V 都使用了双缓冲区。然而,这是冗余的:在执行第一次 MMA 时,我们可以预取当前迭代的 V;在执行第二次 MMA 时,我们可以预取下一个迭代的 K。换句话说,我们只需要为 K 使用双缓冲区。
// prefetch K
load_K(0);
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
// prefetch V for current iteration
// now we have 2 prefetches in flight: K-V
// __syncthreads() here is required to make sure we finish using V_smem
// from the previous iteration, since there is only 1 shared buffer for V.
__syncthreads();
load_V(kv_id);
// wait for prefetch of current K and load K shared->registers
// now we have 1 prefetch in flight: V
...
// 1st MMA
...
// prefetch K for the next iteration
// now we have 2 prefetches in flight: V-K
load_K(kv_id + 1);
// online softmax
...
// wait for prefetch of current V and load V shared->registers
// now we have 1 prefetch in flight: K
...
// 2nd MMA
...
}// prefetch K
load_K(0);
for (int kv_id = 0; kv_id < num_kv_iter; kv_id++) {
// prefetch V for current iteration
// now we have 2 prefetches in flight: K-V
// __syncthreads() here is required to make sure we finish using V_smem
// from the previous iteration, since there is only 1 shared buffer for V.
__syncthreads();
load_V(kv_id);
// wait for prefetch of current K and load K shared->registers
// now we have 1 prefetch in flight: V
...
// 1st MMA
...
// prefetch K for the next iteration
// now we have 2 prefetches in flight: V-K
load_K(kv_id + 1);
// online softmax
...
// wait for prefetch of current V and load V shared->registers
// now we have 1 prefetch in flight: K
...
// 2nd MMA
...
}版本 5:attention_v5.cu。
更有效地使用共享内存意味着我们可以增加一些 tile 大小。我将 BLOCK_KV 从 32 增加回 64。增加 BLOCK_Q 很困难,因为它会使保存累加器的寄存器数量翻倍。改进是适度但明显的。
| 内核 | TFLOPS | % of SOL |
|---|---|---|
v4(ldmatrix.x4 用于 K 和 V) | 194.33 | 92.76% |
| v5(更好的流水线) | 197.74 | 94.39% |
下一步是什么?¶
| 内核 | TFLOPS | % of SOL |
|---|---|---|
F.sdpa()(Flash Attention) | 186.73 | 89.13% |
F.sdpa()(CuDNN) | 203.61 | 97.19% |
flash-attn | 190.58 | 90.97% |
| v1(基础版) | 142.87 | 68.20% |
| v2(共享内存重排) | 181.11 | 86.45% |
| v3(2 级流水线) | 189.84 | 90.62% |
v4(ldmatrix.x4 用于 K 和 V) | 194.33 | 92.76% |
| v5(更好的流水线) | 197.74 | 94.39% |
回顾一下,我们的内核 v3 已经击败了官方的 Flash Attention 内核,这是一个不错的惊喜。感觉相比前几代,从 5090 中获得良好性能相当容易。然而,我们最好的内核落后于 CuDNN 的意味着仍有提升空间。我尝试检查了 CuDNN 注意力内核的性能分析数据,并得到了以下细节
- 内核名称:
cudnn_generated_fort_native_sdpa_sm80_flash_fprop_wmma_f16_knob_3_64x64x128_4x1x1_kernel0_0-> 我猜这意味着使用 sm80 特性,BLOCK_Q=BLOCK_KV=64,DIM=128,和 4 个 warps(与我们的内核 v5 相同)。 - 共享内存:40.96 Kb -> 那是
40960 / (64 * 128 * 2) = 2.5乘以(BLOCK_KV, DIM)。缓冲区的小数数量相当奇怪。或者他们的内核更像是BLOCK_KV=32和 5 个缓冲区?我不知道。
无论如何,这里有一些有趣的想法可以在此基础上构建(除了试图击败 CuDNN):
- 实现反向传播(我听说这比前向传播困难得多)
- 量化/低比特注意力,特别是在 5090 上使用 NVFP4。我相信SageAttention 是这个领域的开源前沿。
- 使用 TMA(即
cp.async.bulk)与 warp-specialization 设计。Pranjal 写了一篇不错的博客文章 关于 H100 矩阵乘法的这个主题。 - PagedAttention(即 vLLM 和 SGLang),然后构建一个高性能的无依赖服务引擎。
我希望这篇博客文章对许多人有用。祝编写内核愉快!








